-
Posts
4785 -
Joined
-
Days Won
55
Content Type
Profiles
Forums
Events
Everything posted by joigus
-

Circumventing Newton's third law through Euler Inertial Forces
joigus replied to John2020's topic in Speculations
What about this for exotic assumptions?: I must confess I'm in awe as to the amount of detailed analysis that wiser folks than me are willing to offer you to explain why your idea cannot work. I'm far lazier. That's why I go for the arguments why your idea is a non-starter because it is ill-conceived from the get go, instead of going into the details. Energy can be hidden inside a system and suddenly be released. But momentum is a vector quantity, so it doesn't work that way. Momentum cannot be hidden "under the rug" of internal variables. It also must be conserved for very robust, absolutely fundamental reasons that have been explained to everybody's satisfaction but yours. It is not only a mathematical theorem about symmetries and conservations laws. It has been checked ad nauseam experimentally. It is valid across different theories. It is quite simply how Nature works. The errors have been pointed out to you from every which direction. You are mixing forces that are only valid in a non-inertial frame with forces that are only valid in an inertial frame so that, in your mind, your system can do what you want it to do, never mind it's known to be impossible. When pressed about a fundamental point, you claim that maybe general relativity is wrong, that maybe there is a special place in the universe where the speed of light is null. You use concepts like "quasiparticle" or "bare particle" (that make no sense in the context you're using them) so that your nut-and-bolt system can produce momentum. Nothing in your system can be sensically considered a quasiparticle. Also, you use a mathematical term like dm/dt (a varying mass term implying m(t), only justifyable if there is a continuous mass jettison of some kind) for a mechanical element which actually stays in your system and thus keeps contributing inertia, internal forces, and torques; so it cannot be represented by such term. Neither your system's mass, nor its parts' can be represented by a mass that is a function of time, as all your masses are constants. Now suddenly magnetic fields make an appearance. This looks more and more like one of those open-ended problems, constantly morphing, of which only the conclusions remain constant. What's next? The Dirac equation must be corrected? -
Sorry, I meant "vacuum energy". It is a part of Einstein's general theory of relativity. It is a term responsible for expansion. The farther away galaxies are from each other, the faster the recede from each other. So the "repulsion" (it's not really a repusive force, it's rather space itself expanding) is proportional to the distance. It also depends on time, increasing exponentially with it, so you would never be able to compensate for it by gathering mass locally. Expansion of the universe will always win eventually, no matter how much mass you cluster together to compensate for it.
-
Why do you say all space-time to be curved is inside the mass? (My emphasis.) I'm interested in your question, but I need clarification of the previous point.
-
I agree that there are important differences. I said that in the spirit of an analogy, which was --I think-- Swansont's original intention. Many physical systems look inert, but they have certain "tension" stored in them. A rubber band, a compressed spring, chemical energy --free energy is the useful concept in the acid's case, rather than potential energy,* as you know very well. In an analogous way, magnets have this tension stored in them. Whether this tension is released to produce work (where there's work, there's force), depends on the presence of other magnets. Once you put a magnetic dipole in front of a magnet, there is a potential energy of interaction that depends both on the distance and the relative orientation of both. The most elementary version of this potential energy is that between a magnetic dipole and a magnetic field: https://en.wikipedia.org/wiki/Potential_energy#Magnetic_potential_energy The OP, and then Charles, seemed to be confused with how something "inert" can produce work. * Although they can be related from a fundamental POV
-
Not enough in the visible universe. You would have to go beyond the cosmic horizon (3-odd billion light years away) and pick up a lot that was lost when the universe was inflating more than a 3-odd billion years ago. And that's impossible. We suspect lots and lots of matter to have been lost forever beyond the cosmic horizon. Other users are suggesting different ways of understanding your question, though. That's interesting. Black holes are usually associated with very intense gravitational fields, but that's because they are behind their horizons; they are extremely compressed. But as pointed out by MigL, the outer field at a distance far enough away is indistinguishable from the field of any other source of the same mass. Be aware though, that the farther away you go, the more intense is the effect of energy vacuum, and the feebler is the "source effect" one. So you would never be able to compensate by accreting local mass. I hope the argument is clear. They pull, not only in different directions, but with opposite varying tendencies depending on the distance. I think that's key to say; no, it would not be possible. Still IOW, you're trying to compensate for k'r with a -k/r2 by playing with k. There will always be a distance r such that your "compensation" breaks down.
-
You can picture magnets as pieces of metal that package circulating currents inside. In the case of ferromagnetism, it's somewhat more involved, because you need quantum mechanics for ferromagnetism to be possible. But you can start by seeing from Maxwell's equations that small magnetic dipoles exert forces on each other, because they have an energy depending on their relative position. Then you should go on to picture the chunck of metal as having many of these little magnetic dipoles aligned with each other. I don't know if that helps. Trying to understand these things with vague concepts like "inert" is perhaps not the best way. As iNow says, magnets are not "inert." Something is "moving" inside so as to keep the fields in place. An as Swanson says too, the magnet, left to itself, looks quiet, but there is some "tension" inside, if you will. The acid example is a very good one. You look at sulfuric acid in a vessel and it looks pretty much inert. But there's a lot of potential energy in it that can cause quite some damage.
-
The point of calculus is studying change and balances of change. The point of Cartesian coordinates is to parametrize space.
-
Magnets do have energy density proportional to the field squared. Maybe the bell that's ringing in your head is that a magnetic field doesn't do work on a moving charged particle. If that's the case, it's true that a magnetic field doesn't do work on a charged particle with velocity v, because the force is perpendicular to the displacement. Magnets acting on each other also have energy.
-
As @MigL says, those are periodic trajectories in phase space, not CTCs. CTCs involve time as a dimension too.
-
I don't understand what you mean. Can you rephrase? On a humorous note, the point of calculus is x.
-
Black holes are very small in relation to their mass. The whole Milky Way is somewhere between 100-200 thousand light years across. Yet its Schwarzschild radius is about 0.31 light years only. On the contrary, the accelerated expansion is only noticeable beyond the range of billions of light years. So black holes would never overcome expansion. The mass would have to be ridiculously big. You can do the comparison yourself. G=6.674×10−11N⋅m2/kg2 c=3×108 ms-1 1 light year = 3×108 ms-1 × 365×24×3600 s M = (1 billion light years)× c2 /2×G Somewhere around 6 × 1042 kg I think. 1030 Milky Ways... Ridiculous A million million million million million Milky Ways. No way.
-
That's what I believe.
-
Nice historical account. Thank you.
-

Circumventing Newton's third law through Euler Inertial Forces
joigus replied to John2020's topic in Speculations
=> Newton pairs => No contribution to overall motion => Not significant to COM evolution equations => Again. Rotation of one part not relevant to COM coordinates motion => No. Fictitious forces only relevant to objects moving with respect to non inertial frames (nut, bolt, etc.) subject to acceleration. Not relevant to COM motion. => Already addressed. Non-sequitur => Already addressed. Non-sequitur That's exactly what I think. There will also be a push and pull effect along the axial direction, to be studied in terms of action and reaction, if you will. Again: no overall momentum. Even though the detailed analysis would be quite involved. Assuming there's no friction, any angular displacement would result in a linear displacement, depending on the pitch of the screw. As said, and so far unanswered, the Lagrangian formalism makes it quite transparent that there can be no thrust for the COM system. It is true that the Lagrangian formalism can only be applied to conservative systems. But friction would only make it worse, not better, for the OP's claims. -

Circumventing Newton's third law through Euler Inertial Forces
joigus replied to John2020's topic in Speculations
You cannot dismiss essential points by saying they are "just assumptions" (to be addressed later) and then rush to mention in passing Planck's length (or a tiny fraction of it?), alleged axial anysotropies in the CMB (unobserved), etc. and then expect everybody to believe these bizarre phenomena that would require a complete re-work of everything physics is based on, all coming from a simple diagram. Your machine cannot turn the world as we know it upside down in one fell swoop. The physical principle you're up against is even valid for systems of quantum fields and is a version of Ehrenfest's theorem. I would (and will) demand nothing short of arguments of such dazzling clarity as to make me think it's worth giving up everything I've learnt during a lifetime. 1) Momentum conservation is tied to space symmetries 2) Fictitious forces only appear in non-inertial systems 3) Internal constrictions can always be resolved into action-reaction pairs in the inertial frame (I told you why this is necessary to be able to apply Newton's laws either to whole systems or to their constituent parts) 4) Mass transfer only results in thrust when mass is permanently ejected, not when it's kept inside the system May I also remind you of the adage, "Extraordinary claims require extraordinary evidence." Carl Sagan -

Circumventing Newton's third law through Euler Inertial Forces
joigus replied to John2020's topic in Speculations
In what frame of reference? Ficticious forces only appear (as apparently reaction-less) in non-inertial frames. Are you sitting on the turning "nut" whence you're going to measure your ship's overall motion? That would be inconsistent. This very much reminds me of another thread in which a user has been rejecting special relativity for years due to the mixing in his mind of lines of reasoning that can only be applied to one or the other frame of reference. -

Circumventing Newton's third law through Euler Inertial Forces
joigus replied to John2020's topic in Speculations
In what frame of reference? You don't seem to be aware that accelerations are frame-dependent. You've been asked this before, I think. In a FOR sitting with the ship initially at rest there are no fictitious forces. There are Newton pairs, and they cancel. In the Lagrangian formalism, they're expressed as some kind of integrable constraint: f_1(angle)d(angle) = f_2(angle')d(angle') and they don't appear in the COM motion. You don't even have to think about them as "forces." Technically we know them as "ignorable coordinates." I wonder why. Edit: https://en.wikipedia.org/wiki/Noether's_theorem#Historical_context (My emphasis.) Edit 2: Well, they don't "cancel," as @swansont pointed out on a previous thread, as each acts on a different part of the system. But they can vectorially be added up in the eqs. of the overall motion and don't play a role at all in its COM motion. Sorry, I made a mistake. Ignorable coordinates are the COM coordinates (they don't appear in the Lagrangian.) The other aspect is the constraint: f_1(angle)d(angle) = f_2(angle')d(angle') So that the constraint is integrable and you can describe the internal motion by just one coordinate. Which doesn't appear in the potential energy (because there is no external potential) so that it is, in fact, ignorable too. -

Circumventing Newton's third law through Euler Inertial Forces
joigus replied to John2020's topic in Speculations
Do you realise that, provided the total system maintains its mass, and none is ejected to space, statements 4. and 5. are in mutual contradiction? -
Thank you for the references. Yes, this (mild) scepticism has been in the air for quite some time. Back in year 2000 you simply could not say you had problems with Copenhagen's interpretation without being classed as a heretic. It was dogma, no doubt due to its astonishing calculational power. Adding to it was Von Neumann's impressive authority on the matter, that went almost unchallenged for decades. It is my posture that the standing uneasiness can be addressed through a concept sketched by John Bell's (one of the first Copenhagen's sceptics) notion of beables. If you wholeheartedly accept the fundamental complex-number mapping of "reality" that QM persistently suggests, you can complex-parametrize these states (the way you usually do in QM) and further assume that part of these quantum-dynamical variables can never be measured --overall phase, gauge arbitrariness, spin projections that are not being measured... What you see in an experiment would just be certain real-number projections of these essentially complex states. IOW, any physical system would package a residual internal entropy that cannot be set to zero by experimental determinations. Again (mathematically) IOW: Quantum states can be set in eigenstates of complex operators that are not Hermitian (those would be the beables, what physical systems "are",) but measuring processes (and their outputs) must be represented by Hermitian operators and their eigenvalues (those would be the observables, what systems "look like" to other systems, which we can call observers.) That would be the reason why pure quantum states cannot be generally purely, unambiguously, "coloured" (in my analogy). They would be chameleonically coloured (in your 1st-reference's parlance.) They always look "coloured" whenever I look at them. But they are only "complex-coloured" internally. Still IOW: they have complex colours; I only see real colours.
-
Exactly my usual points about this question. Correlations are there since the very start of the state preparation. So nothing non-local is implied. This is the problem: Suppose elementary particles (say, electrons) are coloured balls. Balls can be found to be in any colour state as referred to a basis R, G, B, and you have devices to measure this "colour." You set both balls to be in an overall state that is white (colourless). So there is perfect anticorrelation; when one of them is found to be at R (total redness) the other one is found to be at GB (total anti-redness). For this you need a specific "redness" detector. But you can not say the ball was red before you measured its level of redness. And the reason is that whenever you measure a different colour component (say, brownness) the particle appears to be either brown or anti-brown (whatever that decomposition is in the RGB basis.) You see our predicament: How did the particle "know" I was going to measure the level of "brownness"? If my particle produced "anti-brown," sure enough, the other one produces "brown." The problem, thus, is not any communication bridge between the particles. The problem is your classical mind: Your classical mind demands the particles to possess an attribute (namely, definite colourness) that is not there. The property that is packaged in the quantum state is a predicate about both particles, which, when referred to your classical mind, can only be expressed as this predicate: "Whatever the colourness of particle (1) is measured, particle (2) will produce the corresponding anti-colourness if the same colourness component is measured." You can write down this property quite simply: J = C_i(1) + C_i(2) = 0 for any possible i-projection in the colour space. But you cannot attribute any particular C_i(1) or C_i(2) separately.
-

Circumventing Newton's third law through Euler Inertial Forces
joigus replied to John2020's topic in Speculations
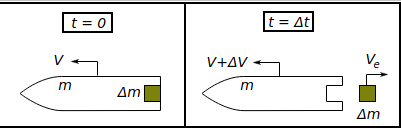
Here's the essence of mass transfer as applied to obtaining thrust: In your system. Where does delta(m) go? If delta(m) stays in the system. How does it cyclically go back while the net result being to impinge some momentum to the whole system in every cycle? The three of us, @swansont, @Ghideon , and myself, have expressed interest in this question, at some point, and I think all of us sense an underlying confusion between two very different kinds of so-called "reactions." Can you, please, address this in some detail so that we can proceed to other points? Edit: I took a quick screenshot from the Wikipedia image, https://upload.wikimedia.org/wikipedia/commons/4/42/Var_mass_system.svg as the SVG format doesn't display well. -

Circumventing Newton's third law through Euler Inertial Forces
joigus replied to John2020's topic in Speculations
First, there is no centre of the universe. The universe is pretty much homogeneous and isotropic on the scale of super-clusters. What you say contradicts GR, which we know to be a very good approximation to the large-scale structure of the universe. Second, if such "centre" existed, and the angular velocity increased as you approached it, there would be noticeable optical effects, as well as on the CMB. Third, a null speed of light anywhere is inconsistent with relativity, which you use in your paper. Fourth, how you relate quasi-particles (the domain of which are many DOF systems) with your 2 DOF system is completely obscure to me. Is this a new physical concept? If so, how do you define it in such a way that it doesn't coincide with the common concept of quasi-particles? I stated it because the impossibility to obtain momentum "for free" is valid even in contexts where Newton's 3rd law is no longer valid. You seem to be forced to appeal to cosmological models that you haven't justified or mentioned, but in passing, and after you were pressed for explanation. If you're going to change the very concept of space and claim the existence of a special "centre of the universe", why not mention it from the start? Conservation of total momentum is a consequence of the action for the system not depending on COM coordinates. I'm not aware that your model depends on cosmic coordinates. Where in your diagram are those cosmic coordinates? It doesn't show up in the model. Your mentioning of coordinates relative to a "centre of the universe" came from out of the blue when you were pressed to explain your model as relates to general conservation principles. -

Circumventing Newton's third law through Euler Inertial Forces
joigus replied to John2020's topic in Speculations
As Swansont says, non-inertial forces only appear in a non-inertial reference frame. If you want to analyse whether momentum can appear for the COM frame, you must set yourself on an inertial frame. And you'll see it can't. These reciprocal Newton pairs disappear from the overall motion. The Lagrangian treatment makes all this very transparent. Is this your pre-print?: https://vixra.org/pdf/2010.0034v1.pdf In this paper, either you, or someone who's of the same mind than you, try to extend the concept to special relativity. It doesn't work either. In the realm of SR, neither Newton's third law is valid, nor the concept of force is useful anymore. But the impossibility of getting COM motion from internal actions persists. So you're up against something very deep and very robust. I don't know what an "Euler inertial force" is. But googling for it produced this pre-print and a handful of other results (only 2 Google pages.) It doesn't seem that the scientific community is very much aware of this concept. Inertial (fictitious) forces are relevant when you have external fields (centrifugal barriers come to mind.) But the planet that's falling in the grav. field of a star is not an inertial reference frame --consistently with Swansont's assertion. They are also relevant if you try to walk on a merry-go-round (centrifugal and Coriolis), but again, you're not in an inertial reference system. A merry-go-round's COM cannot start moving as a whole as a consequence of (internal) Coriolis and centrifugal forces. A spinning top can move, but it's subject to external forces (friction.) What you suggest would require to totally rethink the concept of space. This goes deep. -
Infinitely many times differentiable. Exactly. It's a topological concept. Its adherence (the set of all its accumulation points = points that can be reached by limits) is contained in it. Sorry, I don't understand. Interferrable?
-
? (My emphasis.) By highly mathematical I meant something like one of my old teacher's book on exact solutions in GR. It started with "the universe is a C-infinity differentiable manifold, dense, simply connected and boundary-less" --something like that.