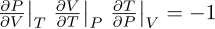joigus

This very much converges with what I was thinking --even being an absolute nuthead when it comes to geology. The Himalayas are very much geologically active. They are very "plastic," so to speak. Erosion is at its maximum Earth-wise (you just have to take a look at the Kali Gandaki gorge.) I'm sure swathes of relatively young or "uncooked", sedimentary, non-metamorphic rock are being exposed too. But I must confess I'm not sure by any means... Eons of rock formation are being stripped away there. What do you guys think?

You are, as Endy0816 says, considering the work done by an ideal gas in an isothermal expansion or compression. Following your notation, \[\tau=-\int PdV=-\int P\left(V\right)dV\] So that, \[\tau=-\int nRT\frac{dV}{V}=-nRT\log\frac{V_{2}}{V_{1}}\] The reason why that procedure is only valid for reversible processes is that if you want to be able to guarantee that the equation of state \[f\left(P,V,T,n\right)=\frac{PV}{nRT}=\textrm{constant}=1\] is valid throughout the process, it must take place under equilibrium conditions throughout. In other words, the control parameters must vary very slowly compared to the relaxation times of the gas, so that it constantly re-adapts to the "differentially shifted" equilibrium conditions. Those are called "reversible conditions". Chemists use the word "reversible" in a slightly different sense, so be careful if your context is chemistry. Exactly.

I was quasi-quoting Dan Britt in Orbits and Ice Ages: The History of Climate. Conference you can watch on Youtube. You got me: argument of authority, I should be ashamed of. Conversations with you are starting to get very stimulating. Thank you very much for the references. I'll reconnect in about 5+ hours, then learn geology in about a couple of hours, and then keep talking with you, hopefully. The bio-data I got mostly from https://www.amazon.com/Life-Science-William-K-Purves/dp/0716798565 and a wonderful MIT course by Penny Chisholm.

I understand how you can say that. But it's not that clear to me. First, dinosaurs, like any other megafauna, are almost anecdotal in terms of primary production, carbon cycle, etc. To give you an example, there are about ten trillion tons of methane stored in the oceanic bottoms that can't get out thanks to methane-metabolizing microscopic archaeas that are keeping it at bay. And, mind you, methane is 25 times more greenhouse-effect inducing than CO2 is. If you want to understand ecosystems you must look at microorganisms. They don't look as pretty in a theme park, but are far more important for the global chemistry. Another question is the rate at which this is happening. Back in the time of the dinosaurs the conditions were quite stable, and many big animals (quite a big bunch of them in terms of animal biomass) may have been slow-metabolism. As to the dinosaurs, we don't really know if they were or how many there were. We do know that all the plants were C3, because C4 plants did not exist. How did that affect the carbon cycle? Be aware, e.g. that RubisCO, the carbon-fixating molecule, is the most abundant organic molecule on Earth by far. In fact, C4 plants, which are more efficient at sucking up CO2 from the atmosphere, precisely evolved to adapt to the new, slowly-changing, low-CO2 atmospheric conditions. And that's the observation that leads me back to the question of rate. Organisms need time to adapt, measured in tens of millions of years, not decades, for those paradises that you picture in your mind to establish themselves. We are now pumping into the atmosphere an estimated billion tons of CO2 per year. The Earth is 100 years within a Milankovitch cycle of glaciation, and yet the glaciers are clearly melting, and fast. We are really fortunate that the Himalayas are still pushing up, because this geological process sucks CO2 from the atmosphere at an incredible rate, and sends it back to the sea. The really big question now is what will happen when the ice sheet on Greenland sloshes down to the North Atlantic, as it is sure that the salinity will go down significantly and the conveyor belt that equilibrates the water temperature will eventually stop. It is estimated that that will happen by 100 years' time. Have you thought in any depth about these and other factors?

I totally agree. In fact, in the topics of physics that are dearest to my heart, it is my conviction that we must overcome this concept. I see your point. I went back to my sentence and I think what I meant (or must have, or should have meant) is "The culprit of all this is the fact that thermodynamics always forces you to consider energy." Instead of, No, I haven't, but from perusing the first pages --although the energy arguments weren't there--, it looks like a very interesting outlook. It reminds me of what Perelman did to solve the Poincaré conjecture: consider the Ricci flow to prove a topological statement. That's using a physical idea to solve a mathematical problem. I would talk more about this delightful topic, but my kinetics is forcing me to slow down. Maybe later. It's been a pleasure.

I have to agree with studiot's disagreement. That's one of the most common obfuscations when studying thermodynamics (TD). In TD you never go outside the surface of state, defined by the equation of state f(P,V,T,n)=0. That's why they most emphatically are not independent variables. This is commonly expressed as the fundamental constraint among the derivatives: which leads to unending "circular" pain when trying to prove constraints among thermodynamic coefficients of a homogeneous substance, for teachers and students alike. 'Kinetics' is kind of a loaded word. Do you mean dynamics vs kinematics in the study of motion, or as in 'kinetic theory of gases', 'chemical kinetics'? Sorry, I really don't understand. But I would really be surprised that a theory about anything in Nature missed the energy arguments. Sometimes you can do without it, but there are very deep reasons for energy to be of central importance. I would elaborate a bit more if you helped me with this.

I concur with swansont. Only, I think he meant, W = - delta(PV) assumes constant P when he said, as W = -P(delta V) is just the definition of work for a P, V, T, n system (the simplest ones.) And when n, T are constant ==> d(PV)=0 ==> W = -pdV = +VdP (for that case in an ideal gas.) Just to offer a mathematical perspective. If you differentiate (increment) PV=nRT, you get PdV+VdP = nRdT (d=your "delta"=increment, small change) or for varying n, PdV+VdP = RTdn+nRdT because, as swansont says, you must know what's changing in your process, and how. You see, in thermodynamics you're always dealing with processes. To be more precise, reversible processes (That doesn't mean you can't do thermodynamic balances for irreversible processes too, which AAMOF you can.). Whenever you write "delta," think "process." So, as swansont rightly points out, what's changing in that process? The culprit of all this is the fact that physics always forces you to consider energy, but in thermodynamics, a big part of that energy is getting hidden in your system internally, no matter what you do, in a non-usable way. This is very strongly reflected in the first principle of thermodynamics, which says that the typical ways of exchange of energy for a thermal system (work and heat) cannot themselves be written as the exchange of anything even though, together, they do add up to the exchange of something (here and in what follows, "anything," "something," meaning variables of the thermodynamic state of a system: P, V, T, PV, log(PV/RT), etc.) So your work is -PdV, but you can never express it as d(something). We say it's a non-exact differential. It's a small thing, but not a small change of anything The other half of the "hidden stuff" problem is heat, which is written as TdS, S being the entropy and T the absolute temperature, but you can never express it as d(something). Again, a non-exact differential. And again, A small thing, but not a small change of anything Enthalpy and Gibbs free energy are clever ways to express heat exchange and work as exact differentials, under given constrictions for the thermodynamic variables. And Helmholtz's free energy is something like the mother of all thermodynamic potentials and its true pride and joy.

Yes, taeto, you are right, unless I'm too sleepy to think straight. The thing that's missing in your argument is the transformation matrix, which is, I think, what you mean by, I don't know if you're aware of it, but any Gauss reduction operation can be implemented by a square non-singular matrix. A change-of-basis or "reshuffling" matrix. Let's call it D. So that, AB = ADD-1B = A'B' The "indexology" goes like this: (mxn)x(nxm) = (mxn)x(nxn)x(nxn)x(nxm) The first factor would be an upper-triangular matrix (guaranteed by theorem that I can barely recall) but, as it has fewer columns than rows, at least the lower row must be the zero row, so that the product must have a zero row. Right? (AAMOF you can do the same trick either by rows on the left or columns on the right; it's one or the other. Then you would have to apply a similar reasoning to B instead of A, you're welcome to fill in the details.) This is like cracking nuts with my teeth to me, sorry. That's what I meant when I said, But that was a very nice piece of reasoning. It's actually not a change-of-basis matrix, but a completely different animal.

You may be right. Dimensional arguments could work. Let me think about it and get back to you in 6+ hours. I have a busy afternoon. Thank you!

Gaussian elimination does not help here. The reason being that it requires you to reduce your matrix to a triangular form, and in order to do that, you need the actual expression of the matrix, not a generic amn

My same impression.

How can a continuum be a constant? Could you elaborate on that? Maybe you're on to something. Can a stone be unhappy? See my point? If there is **one** feature of gravity that singles it out from every other force in the universe is the fact that you can always locally achieve absence of gravity (equivalence principle, EP). The only limit to this is second-order effects, AKA tidal forces. Jump off a window and you'll find out about EP. Get close to a relatively small black hole and you'll find out about tidal forces. Read a good book and you'll find out about how this all adds up. Oh, and mass is not concerned at all in GTR, as it plays no role in the theory. It's all about energy. It's energy that provides the source of the field. What you call mass is just rest energy, and this is no battle of words. Photons of course have no mass because they have no rest energy; and they have no rest energy because... well, they have no rest. Incorrect: Special Relativity (SR) says nothing (massless or not) can travel faster than the speed of light. Because GTR says geometry of space-time must locally reduce to SR, things moving locally can't exceed c. In other words: things moving past you can't do so at faster than c. People here have been quite eloquent so I won't belabor the point. I don't want to be completely negative. My advice is: Read some books, with a keen eye on experimental results; then do some thinking; then read some more books; then some more thinking, and so on. Always keep an eye on common sense too. Listen to people who seem to know what they're talking about, ask nicely for inconsistencies and more information, data. Always be skeptic, but don't just be skeptic. It doesn't lead anywhere.

Sorry, I meant And d2/dx2 of (0 0 1 0 0 0) is (2 0 0 0 0 0) just as d2/dx2 of x2 is 2 times 1.

Depends on what they want to illustrate with it. Do you mean state of uncertainty? It's actually a paradox that cosmologists face every single day. No down-to-Earth physicists worry about it, because they use the quantum projection, or collapse, or wave packet reduction, as you may want to call it. They know whether the cat is dead or alive. As to cosmologists... who was looking at the universe when this or that happened, you know? It's not useful for anything, it's just there, looking us in the face. It's a pain in the brain. . Yes. No.

If you are a future mathematician, I would advise you not to try to think of the cotangent space as something embedded in the space you're starting from. In fact, I bet your problem is very much like mine when I started studying differential geometry: You're picturing in your mind a curved surface in a 3D embedding space, the tangent space as a plane tangentially touching one point on the surface, and then trying to picture in your mind another plane that fits the role of cotangent in some geometric sense. Maybe perpendicular? No, that's incorrect! First of all try to think in terms of intrinsic geometry: there is no external space embedding your surface. Your surface (or n-surface) is all there is. It locally looks to insiders like a plane (or a flat space). What's the other plane? Where is it? It's just a clone of your tangent plane if you wish, that allows you to obtain numbers from your vectors (projections) in the tangent plane. It's the set of all the vectors you may want to project your vector against, therefore, some kind of auxiliary copy of you tangent space. That's more or less all there is to it. Sometimes there are subtleties involved in forms/vectors related to covariant/contravariant coordinates if you wish to go a step further and completely identify forms with vectors when your basis is not orthogonal. That's why mathematicians have invented a separate concept. Also because mathematicians sometimes need to consider a space of functions and the forms as a bunch of integrals (very different objects). In the less exotic case, the basis of forms identifies completely with the basis of contravariant vectors. I will go into more detail if you're curious about it or send you references. I hope that helps.

1) "How fast the shark is moving away from the lifeguard station" requires you to think about vectors. Picture an imaginary straight line lifeguard-shark and try to think how it changes. 2) The datum is the speed or rapidity (the norm, or intensity, or "modulus" of the vector), not that velocity. That's another line (parallel to the coast.) 3) Think Pythagoras. He was a very wise guy, or maybe a bunch of guys, nobody knows to this day. And I can't give you any more clues.

I see no significant mistake in the enunciation of the principle. I wouldn't include time to it though, nor do I know of any formulation that does. Another hopefully useful observation is that isotropy everywhere implies homogeneity, which is kind of more economic to me, but not really a big deal. As to current limits to its application/validity/solidity, I hope you find interesting my comments below: The whole issue of the universe being homogeneous and isotropic at 'large' scales is, in my opinion, a very suspect hypothesis. It looks kind of reasonable, though, and allows you to gain access to the big picture of what goes on. But 1) from the theoretical perspective we do know that quantum field theory (QFT), when combined with the general theory of relativity (GTR) in inflationary models, predicts a universe that is more like a fractal, meaning a scale-independent series of embedded structures that may look clustering depending on what scale you look at it. And 2) from the observational point of view, the universe does seem to display huge voids in its structure, very strongly resembling that fractal that QFT+GTR predicts. It's more like the caustics in a swimming pool in 3D (this is a numerical simulation): About isotropy, a very recent piece of news from the experimental front is this: https://phys.org/news/2020-04-laws-nature-downright-weird-constant.html?fbclid=IwAR3_NdXDNfcNU05E8khtN1pnshucr-gr7KoJO5OTh6OAuDDX19Z5yUBPD_c The headline reads, "New findings suggest laws of nature 'downright weird,' not as constant as previously thought". UNSW --Sidney-- professor John Webb: "We found a hint that that number of the fine structure constant was different in certain regions of the universe. Not just as a function of time, but actually also in direction in the universe, which is really quite odd if it's correct... but that's what we found." If that's true, not only the universe wouldn't be homogeneous; it wouldn't be isotropic either, and at the deepest level, because what's different is the electromagnetic coupling constant itself. Now this would really be amazing and we should take it with a grain of salt. The statement that the universe is homogeneous in time is tantamount to saying that it looked pretty much the same in the past than now or in the future. It was obviously not the same in the past, as it looked like a singularity, then opaque to radiation and neutrinos (plasma), then radiation dominated, then matter dominated, and today it's considered to be dark-energy dominated. So it doesn't really look like it's going to be the same in the future, as it will exponentially expand.

I don't know whether you're familiar with index notation. If you are, I think I can help you. If you aren't, I can't, because it's just too painful. They will have told you about Einstein's summation convention. Don't use it for this exercise, because if you do, you're as good as lost. The key is: you need m indices that run from 1 to m, and another bunch of m indices that run from 1 to n You also need the completely antisymmetric Lévi-Civita symbol: Now, the index that runs from 1 to n (the inner product index) I will call K1, ..., Kn The other multi-index I will call i1,...im And the third one, the second free index, I will fix to be 1, ..., m Then, Now it takes a little insight: The last factor is the det of m vectors in an n-dimensional space. As m>n, it is therefore a linearly dependent set, so it must be zero. You can understand this better if you think of the det as a multilinear function of m vectors.

Well, yes, but you must be careful with a couple of things. First: If you integrate x5 you get off limits. x6 no longer is in your space. You must expand your space so as to include all possible powers. . Then you're good to go. Second: You must define your integrals with a fixed prescription of one limit point. For example, so that they are actually 1-valued mappings. Then it's correct. You don't have this problem with derivatives, as you can derive number zero till you're blue in your mouth and never get off limits. If you were using functions other than polynomials, you would have to be careful with convergence of your integrals. But polynomials are well-behaved functions in that respect. Hope it helps.

You're right, there is a theorem. It's really to do with the fact that you've got a linear isomorphism, that is, a mapping such that, that is, that preserves the linear operations in your initial space. Your initial space must be a linear space too under (internal) sum and (external) multiplication by a constant. Now, objects A, B, etc. can be most anything. They can be polynomials, sin cos functions, anything. The key facts are both that the d/dx operator is linear and the polynomials under sum and product by scalars are a linear space. The would be assigning a vector to a polynomial. And your intuition is correct. There is no limit to the possible dimension of a linear space. Quantum mechanics, for example, deals with infinite dimension spaces, so the transformation matrices used there are infinite-dimensional matrices. In that case it's not very useful to write the matrices as "tables" on a paper. I hope that helps.

Exactly right. Check it yourself. It's a fun exercise. On that space, the diff operator "is" the matrix.

Exactly. 1 would be (1 0 0 0 0 0), x: (0 1 0 0 0 0), x2: (0 0 1 0 0 0), etc. (read as column vectors). And d/dx of (0 0 1 0 0 0) is (2 0 0 0 0 0) just as d/dx of x2 is 2 times 1.

Depends on how you order your basis. Let's say {1,x,x2,...} (I'd pick a 'natural' basis, meaning one in which your matrix looks simpler, of course any non-singular linear combo of them would do). The transform of xn is n(n-1)xn-2, so what it does is to multiply by n(n-1) and shift it twice to the right (here's where the ordering of you basis matters in what the matrix looks like, so if you order the other way around, the T --transformation-- matrix would look like the transpose). So your matrix would be something like, That is, Please, check. I may have made some ordering mistake, missed a row, etc.