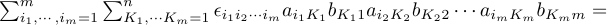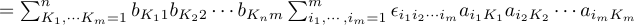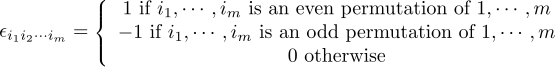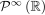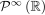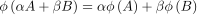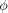-
Posts
4785 -
Joined
-
Days Won
55
Content Type
Profiles
Forums
Events
Everything posted by joigus
-
1) "How fast the shark is moving away from the lifeguard station" requires you to think about vectors. Picture an imaginary straight line lifeguard-shark and try to think how it changes. 2) The datum is the speed or rapidity (the norm, or intensity, or "modulus" of the vector), not that velocity. That's another line (parallel to the coast.) 3) Think Pythagoras. He was a very wise guy, or maybe a bunch of guys, nobody knows to this day. And I can't give you any more clues.
-
I see no significant mistake in the enunciation of the principle. I wouldn't include time to it though, nor do I know of any formulation that does. Another hopefully useful observation is that isotropy everywhere implies homogeneity, which is kind of more economic to me, but not really a big deal. As to current limits to its application/validity/solidity, I hope you find interesting my comments below: The whole issue of the universe being homogeneous and isotropic at 'large' scales is, in my opinion, a very suspect hypothesis. It looks kind of reasonable, though, and allows you to gain access to the big picture of what goes on. But 1) from the theoretical perspective we do know that quantum field theory (QFT), when combined with the general theory of relativity (GTR) in inflationary models, predicts a universe that is more like a fractal, meaning a scale-independent series of embedded structures that may look clustering depending on what scale you look at it. And 2) from the observational point of view, the universe does seem to display huge voids in its structure, very strongly resembling that fractal that QFT+GTR predicts. It's more like the caustics in a swimming pool in 3D (this is a numerical simulation): About isotropy, a very recent piece of news from the experimental front is this: https://phys.org/news/2020-04-laws-nature-downright-weird-constant.html?fbclid=IwAR3_NdXDNfcNU05E8khtN1pnshucr-gr7KoJO5OTh6OAuDDX19Z5yUBPD_c The headline reads, "New findings suggest laws of nature 'downright weird,' not as constant as previously thought". UNSW --Sidney-- professor John Webb: "We found a hint that that number of the fine structure constant was different in certain regions of the universe. Not just as a function of time, but actually also in direction in the universe, which is really quite odd if it's correct... but that's what we found." If that's true, not only the universe wouldn't be homogeneous; it wouldn't be isotropic either, and at the deepest level, because what's different is the electromagnetic coupling constant itself. Now this would really be amazing and we should take it with a grain of salt. The statement that the universe is homogeneous in time is tantamount to saying that it looked pretty much the same in the past than now or in the future. It was obviously not the same in the past, as it looked like a singularity, then opaque to radiation and neutrinos (plasma), then radiation dominated, then matter dominated, and today it's considered to be dark-energy dominated. So it doesn't really look like it's going to be the same in the future, as it will exponentially expand.
-

Determinants : Proof det(AB)=0 where Amxn and Bnxm with m>n
joigus replied to Javé's topic in Linear Algebra and Group Theory
I don't know whether you're familiar with index notation. If you are, I think I can help you. If you aren't, I can't, because it's just too painful. They will have told you about Einstein's summation convention. Don't use it for this exercise, because if you do, you're as good as lost. The key is: you need m indices that run from 1 to m, and another bunch of m indices that run from 1 to n You also need the completely antisymmetric Lévi-Civita symbol: Now, the index that runs from 1 to n (the inner product index) I will call K1, ..., Kn The other multi-index I will call i1,...im And the third one, the second free index, I will fix to be 1, ..., m Then, Now it takes a little insight: The last factor is the det of m vectors in an n-dimensional space. As m>n, it is therefore a linearly dependent set, so it must be zero. You can understand this better if you think of the det as a multilinear function of m vectors. -
Well, yes, but you must be careful with a couple of things. First: If you integrate x5 you get off limits. x6 no longer is in your space. You must expand your space so as to include all possible powers. . Then you're good to go. Second: You must define your integrals with a fixed prescription of one limit point. For example, so that they are actually 1-valued mappings. Then it's correct. You don't have this problem with derivatives, as you can derive number zero till you're blue in your mouth and never get off limits. If you were using functions other than polynomials, you would have to be careful with convergence of your integrals. But polynomials are well-behaved functions in that respect. Hope it helps.
-
You're right, there is a theorem. It's really to do with the fact that you've got a linear isomorphism, that is, a mapping such that, that is, that preserves the linear operations in your initial space. Your initial space must be a linear space too under (internal) sum and (external) multiplication by a constant. Now, objects A, B, etc. can be most anything. They can be polynomials, sin cos functions, anything. The key facts are both that the d/dx operator is linear and the polynomials under sum and product by scalars are a linear space. The would be assigning a vector to a polynomial. And your intuition is correct. There is no limit to the possible dimension of a linear space. Quantum mechanics, for example, deals with infinite dimension spaces, so the transformation matrices used there are infinite-dimensional matrices. In that case it's not very useful to write the matrices as "tables" on a paper. I hope that helps.
-
Depends on how you order your basis. Let's say {1,x,x2,...} (I'd pick a 'natural' basis, meaning one in which your matrix looks simpler, of course any non-singular linear combo of them would do). The transform of xn is n(n-1)xn-2, so what it does is to multiply by n(n-1) and shift it twice to the right (here's where the ordering of you basis matters in what the matrix looks like, so if you order the other way around, the T --transformation-- matrix would look like the transpose). So your matrix would be something like, That is, Please, check. I may have made some ordering mistake, missed a row, etc.
-
Please, don't apologize. I wasn't making much sense biologically, and now I realize that I'm confusing really basic stuff in RNA maturation process. I really must go over my notes and books before I make more of a mess and take much more of your time. What does make sense in what I'm saying, I think, is that different reflection symmetries in the chain to be cut must play an important role in the cutting process, because the enzyme's job is to cut a line of covalent bonds, so a very high energy barrier must be overcome. As CharonY says: (my emphasis) So the general idea that I get from these comments is something like: Oh, so the enzymes that do the job of cutting must either twist the strand, bend it, then act like scissors... Now, these physical actions all require some handling of the object with different configurations of strong opposite pairs of force. This is very different from what is required in, e.g., helicases, which only need to overcome hydrogen bonds to untangle the double strand for reading and don't require any kind of symmetric grasping of the molecule that I can think of. In one of the images that you so kindly (but so much overestimating my understanding of biology) have attached, I've found something very interesting. I can see a single-stranded sequence under the tag hsa-miR-25-5p that reads, TCCGCCT Now, I don't know what the significance of that sequence is, but it is a palindrome in a different sense than palindromes in double-stranded DNA are. This is a palindrome of itself in the sense of ordinary-language palindromes. I.e., if you read it in a 5'-to-3' direction, instead of 3'-to-5', it doesn't change. The palindromes selected for cutting in double-stranded DNA, for example, are different. They are palindromes only if you apply a sequence of two "inversions". Take, for example, my blah-blah example, AGGCCT First invert (read 5' to 3' instead of 3' to 5'): AGGCCT --> TCCGGA Then complementary invert (A-->T, C-->G, G-->C, T-->A): TCCGGA --> AGGCCT And you're back where you started. The fact that different kinds of palindromes pop up when cutting, twisting, etc. are involved; I don't think is coincidental. Free-energy considerations don't interest me so much at this point, important though they are. Please don't trust me when I say anything strictly biological, as it's well over my head there. And do feel free to drop the conversation at any point if you don't find it useful or revealing or anything. Do 'dimers' here --or elsewhere in biology-- refer to primary structure only? Two symmetrically-placed terciary-structure blobs of protein weakly attached to each other wouldn't be a dimer, would they? My ignorance shows, I know. Thank you very much.
-
Sure. Thanks a lot for your interest. I was referring to the possibility of selectively cleaving sequences in a similar way to how restriction enzymes are used to cleave DNA to mass-produce genomic libraries. In this case, though, the target would be RNA. The only example I know of RNA that has complementary (let's say "locally" double-stranded) sub-sequences is tRNA, and from what I remember cleavage of nucleic acids in Nature only happens on double-stranded sequences, e.g. tRNA cleaved by eukaryotes in the splicing process --and as I've just learnt from the references you provided some archaeas[!?]. In other words: would it be possible to mimic endonucleases' job with tRNA, synthesize them, maybe modify them for human purposes? Sorry I said "opposite" instead of "complementary" and the like. And thanks a lot for the references.
-
Here's an idea that, if too out there, I'd wholeheartedly thank you to dismiss as nicely and informatively as possible. Something that very much drew my attention years ago about restriction enzymes is the fact that they always seem to act on palindromic sequences of DNA, not in the usual language-related sense, but in the sense that, for a bunch of code-bases, the sequences usually (maybe always?) are palindromes of their inverses in the "daughter" thread, like, AGGCCT TCCGGA (Sorry if there's a specially reserved codon there, I wasn't particularly careful in the example.) Now, I don't think that's a coincidence and I'm pretty sure there must be a physical reason for it. My best guess is that there must be a physical action, like a cutting torque at the molecular level (my background is theoretical physics) leading to the controlled chopping of the polymer precisely at that spot. Opposite pulling or pushing forces would lead to that in a way that's very intuitively easy to picture. Does that make any sense at all? If so, could a similar mechanism work for endonucleases on tRNA in opposite sequences attached for splicing? I'm not even sure that tRNA splice at palindromes or even if that's been understood in any detail. Thank you very much in advance.
-

Corona virus general questions mega thread
joigus replied to FishandChips's topic in Microbiology and Immunology
This may be a silly question, but just in case. Can someone tell me if there is the possibility of using RNA-splicing endonucleases like the ones referred to at, https://www.ncbi.nlm.nih.gov/pubmed/18217203 to target specific sections of a known virus in order to deactivate it inside the cell in a similar way that restriction enzymes in bacteria function against their bacteriophages? Maybe by designing or selecting them to look for very specific viral sequences but long enough so that they have a very low repeat probability? Or maybe by methylating the sensitive areas in the self RNA? I don't even remember if RNA is susceptible to methylation, which DNA is. Or maybe both? Is that even possible? Or maybe too out there. I'm not even sure this is the proper place to pose this question. I'm sorry if that's the case. Thanks a lot in advance.