-
Posts
4811 -
Joined
-
Days Won
56
Content Type
Profiles
Forums
Events
Everything posted by joigus
-
https://en.wikipedia.org/wiki/Measure_(mathematics) https://en.wikipedia.org/wiki/Fractal Hausdorff measure (fractals): https://en.wikipedia.org/wiki/Hausdorff_measure I hope that helps.
-
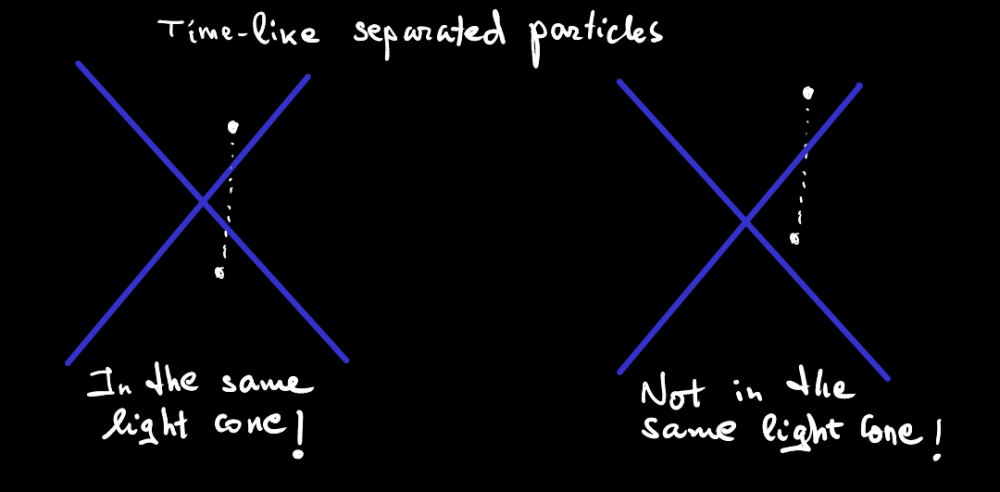
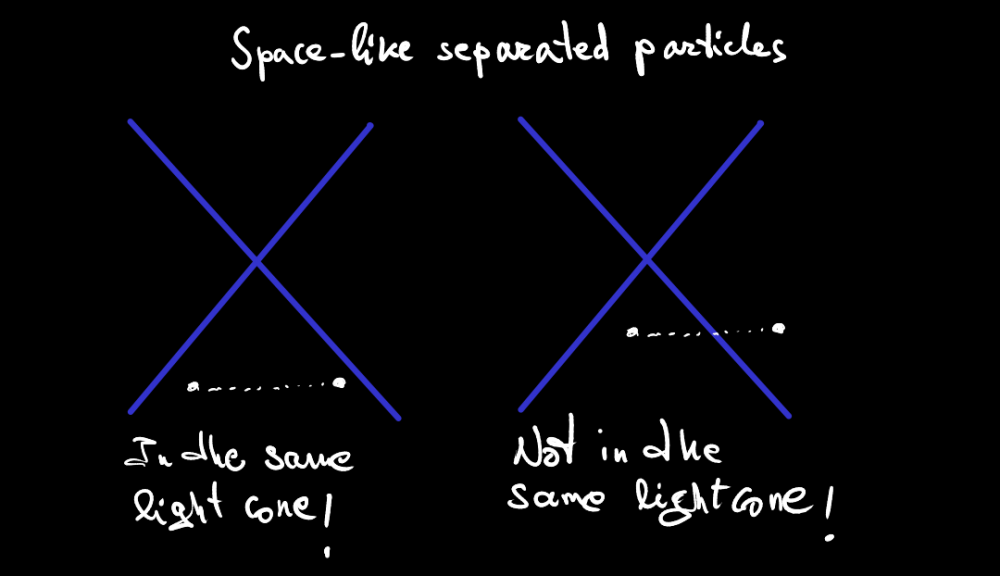
(Emphasis mine.) What do you mean??? Here's a visual aid: Same particles, same events for time-like separated particles. And, Same particles, same events for space-like separated particles. What light cone are you talking about? Same light cone of what exactly? Will you make a smidgen of sense at some point in this simulation of a discussion? I'm ignoring the rest of your nonsense. Let's start with the basics. Otherwise, you're gonna turn everyone crazy here. "Especially electrons..." Yeah, that makes sense too!
-
Same reason why the colour of my sclera, and the colour of yours are the same: Some event in the past determined both. In the example I'm offering you, the evolution of a family of primates. Unless one of us is a possum who's learned to type. Let that be me. Oh, by the way, I've just received a message from next Christmas: Our future selves tell me we are still discussing this.
-
I think Markus meant "measure" in general. There are many cute puzzles like this that are similar and involve other kinds of measures, like Hilbert's curve covering a patch of plane. On the other hand, mathematics based on natural numbers is known to be incomplete, and no theory of this kind can prove its own consistency, so I would relax about the whole thing. Besides, there is no unified set of axioms for all of mathematics, as far as I know. You can relate chunks of it, but not all. I would relax even more. I may be wrong, but I think in this post-Bourbaki era mathematicians tend to be more freely constructive and more deeply involved in guesswork. This has proved to be very fruitful for both physics and mathematics.
-

moment of inertia in round house kick (derivative or integral)
joigus replied to ddddddddd's topic in Classical Physics
What particular physical aspect of the round house kick do you want to understand by means of the moment of inertia? If you want to totally understand the theory of the moment of inertia, you need some integral calculus (although you can do without much) and some vector algebra (perhaps a bit more than calculus.) But qualitative discussion of some simple cases can be done without big mathematical hurdles. -
It absolutely is not a non-local Lagrangian. Let me rephrase without the double negative, which might be confusing: The Lagrangian is totally local. Once the particles start flying apart, you can use free propagation to describe how the fly apart, and the initial entangled state as the initial condition of a so-called Cauchy problem. The Hamiltonian is separable, and contains only 2nd-order spatial derivatives, so local densities, fields, etc are only sensitive to nearby points. It is a 2nd-order polynomial in the spatial derivatives. Local as can be: Exactly the same sensitivity to spatial inhomogeneities as the equation for propagation of heat. And the state keeps entangled all the way. What the classical theory of heat doesn't have, that makes quantum mechanics so peculiar, is, 1) Superposition of several different "heat-radiating states" 2) A multi-system phase space It is the initial condition that cannot be separated, which has consequences on the probabilities that are encapsulated in the state. As Markus said --with my emphasis, Which is exactly what I was trying to say here, This, by the way, you found either very surprising, or implying the opposite of what @Markus Hanke --and I too, many pages before-- is implying: As the probability distributions do not depend on spatial factors while the state is evolving, as it only depends on how the state is interwoven in its spin "tags," how could it encode anything having to do with local (space) properties? Or at least, that is, provided I've understood Markus correctly.
-
The discussion was actually about FTL signals. More in particular, it assumed that FTL signals are actually implied by quantum entanglement. From that as a premise, it proposed the possibility that this "entangled information," whatever that means, can be somehow amplified, or "crowded." It was I who first challenged the premise that FTL signals are possible from the mere basis of QM. @uncool then proposed whether it could be the breaking of quantum coherence --or, if you will, the collapse of the wave function-- that could be used as a signal. Here: That was a very interesting point. I think I basically answered this with a clear resounding "no." But at this point the debate was getting, IMO, very interesting. Then you intervened by entering into a dynamics of a dog chasing his own tail, by repeatedly denying matters of principle and experimental evidence that nobody else here has any significant doubt about. As long as you do not agree on these matters of principle, it will be impossible to further understand why this illusion of non-locality --that's implied, eg, in the last paragraph you quoted-- occurs when one thinks of QM in the terms of Copenhagen's interpretation of the theory. I did try to steer the debate in that direction, because I think it explains the confusion as close as effortlessly as it's possible to do. You stubbornly repeated asking me for a criterion of non-locality after, many posts before, I had already given you one: That you either didn't understand or didn't bother to read. For a theory to actually be non-local, it would have to be a system that, once cast in a Lagrangian form, would have an infinite sensitivity to spatial inhomogeneities. This would reflect in the Lagrangian as having arbitrarily-high order of spatial derivatives. That's why I know quantum mechanics cannot be non-local in any fundamental way, and the whole illusion must come from some kind of basic misunderstanding of the concepts. So it is you who's stalling any progress by repeating over and over some kind of half-diggested undestanding that is not correct and leads anyone who reads it --and believes what you say-- in the wrong direction. Your attitude, from a purely scientific POV, is obnoxious. At one point, it even reached that level from a civil POV, when you indulged in calling people names, when pressed for arguments you were unable to find.
-
Yep. A big +1 to Hanke, as it was a very transparent account of the whole thing. Unfortunately, it's possible that this will not be the last word we hear from Bangstrom, and we get past Xmas still talking about it, to iNow's boredom and despair. We've got now 2 local experts, plus a bunch of other members, plus a panel of distinguished and reputable physicists, who've made their case against a standalone opinion. Can we call it a day?
-
Sorry: I meant "The free non-relativistic Schrödiger equation," of course.
-
The receiver instantly knows if it is “0” or “1” but they can’t know what it means because even the sender can't know what they sent. In other words. You're saying that somehow, what you say is true, just because you say so, but nobody can ascertain experimentally, or even in principle, that it's true. Your simulation of an explanation is more or less the same in all your posts: You somehow know you're right, but you can't quite put your finger on why it's right, or even what exactly it is that you're right about. At this point I'm only just curious about your convictions from a purely psychological point of view. There's certainly no science to be learnt from anything you say here. And again, quantum particles have no identity: https://en.wikipedia.org/wiki/Identical_particles#:~:text=In quantum mechanics%2C identical particles,one another%2C even in principle.
-
The non-relativistic Schrödinger equation in thre dimensions is exactly solvable. It's not deceptive at all what happens in one direction, as it's completely separable. The propagator can be obtained exactly and shows equal dispersion --in empty space-- in every direction, as couldn't be otherwise, because it's completely symmetric under rotations. Because the Schrödinger equation is linear, it has no soliton solutions. You are right though in that other very different things are very different things than the thing I was talking about.
-
I meant "coherence has been lost." Sorry! I do this again and again.
-

Another question about entangled pairs of particles
joigus replied to geordief's topic in Quantum Theory
Sorry, "break coherence." I mix up these opposites from time to time. Yes, I prefer Swansont's answer too. He's as brief as surgically precise. There are many instances in which you learn something about a quantum particle long before you do anything else with it. That's my understanding of filtering, for example. Measurement is not necessarily interaction. But some interaction is necessary at some point, of course, as Studiot just pointed out. Otherwise, as he said, how are you to tell anything about it? Sorry for not having addressed your specific concerns about entanglement. I've been talking about entanglement for like a month. I also have a feeling that some people see in entanglement something that's not involved in the principles of QM themselves, some new law, some extra magic. There isn't. All the mystery is already in the double-slit experiment already, or the "paradox" of partial reflection, etc. I also totally concur with MigL's comments: -

Another question about entangled pairs of particles
joigus replied to geordief's topic in Quantum Theory
What you're suggesting is measuring without interaction or measuring counterfactuals. It's better to deal with it for one particle in the double-slit experiment. You place a detector intercepting particles only in one of the branching paths. You fire your particles one by one and observe where they land in a faraway screen. You gather only the results that didn't do "click" at the detector. You do the statistics of all of those that didn't make the detector click. What's observed is that decoherence is broken. Counterfactual measurements, or interaction-free measurements --as they're also called-- break decoherence. This effect is so real that there is a bomb tester to know if a bomb would go off without actually making it go off: https://en.wikipedia.org/wiki/Elitzur–Vaidman_bomb_tester Sorry for re-directing your question, but I think the essential aspect that you want to understand is contained here more simply than considering entanglement. I hope that has to do with your question at least. Look up for "interaction-free measurement," or perhaps, "counterfactual measurement." Also: https://en.wikipedia.org/wiki/Renninger_negative-result_experiment -
OK, @bangstrom. Enough is enough. Take a code "0" and "1." Describe a protocol that sends either "0" or "1" to a distant observer by using an entangled state. Describe it clearly. It could even be, "0" = "I have performed a measurement" and, "1" = "I have not performed a measurement" So that the distant observer knows immediately it's either "0" or "1" Or, it could be, "0" = "Spin is up along the x-direction" and, "1" = "Spin is down along the x-direction" Or, it could be, "0" = "I have performed a measurement along the x-direction" and, "1" = "I have performed a measurement along a direction other than the x-direction" Describe a protocol that does this without infinitely many data having to be gathered after long hours of painstaking readings, and thereby inferring decoherence has been lost when the STL waiting time has long, long been exceeded. Of course, most of us here understand: (1) That's not possible (2) If it were, SR would be violated But you don't, you don't understand it. You're still clueless after all that's been said. So, please, stop blowing smoke once and for all and give an answer to everybody. Your last paragraphs were some more smoke-blowing and quoting news you don't understand, so I'm not even gonna bother to answer them.
-
No need to apologise. I haven't found you at fault at any point. We respectfully disagree, that's all. I'm very passionate about interpretations of QM. I'm very emphatic about points I've thought about, and read about, for many years. Sometimes, when I see what I perceive as a fundamental misunderstanding of both the facts and the theory, I take issue with it, but in no way it should be understood as hostility. I've seen people's careers destroyed for valiently going down this particular rabbit hole, never to be seen again. It's no joke to me.
-
The state of a particle does not correspond to one wave function. Rather, it is an equivalence class of infinitely many wave functions, all differing in a global relative phase. Further, when you include gauge ambiguity, it's no longer just a global-phase ambiguity, but an infinite collection of local prescriptions for the phase that constitutes the ambiguity. This means that you can attach whatever time-position dependent factor to the wave function, add a counterterm to the gauge field, and the equations of motion are exactly the same. How are you so sure, how is anybody, that factors of this incommensurably infinite group are not relevant to a more complete description of the quantum state? On the other hand, saying that the history of the entire universe is somehow involved in the deflection of, eg, a paramagnetic particle by a Stern-Gerlach magnet is only evidence of how misleading the ongoing blabber about non-locality has been for all these years. Research in beables is a serious branch of theoretical physics, however much making the models falsifiable remains a challenge. Vague assumptions about omniscient agents is not.
-
Because guessing operators more general than Hermitian being relevant to QM is a natural mathematical extrapolation of the postulates of QM, while talking about gods, demigods, and leprechauns is a mythological idiocy with no basis on, relation to, or even suggestions of QM in it. I should think that's next-to-obvious.
-
Emphasis-answered. Seems like I violated causality, because I answered your question before you asked it. @Lorentz Jr, I know it's a lot to ask of anybody to read carefully what came before, but I already mentioned: "weaken the criterion of reality." I'll give you a pointer, if you're interested. The theoretical environment in which similar ideas grow is "loopholes to the impossibility theorems." Keep in mind that impossibility theorems always have premises. If you weaken the premises, you find doors to unexpected landscapes. It's happened before.
-
Every entanglement is different and depends partly upon the conditions of the entanglement. Ghideon's example is classical. But with the wife, socks, gloves and so on you need at least the information that they are married, there is a pair of socks of gloves. Otherwise when the box of gloves is opened the discovery that it contains a right hand glove is of no extra meaning. Yes. Thank you. Very interesting comments. +1 To me the big "mystery" is how the quantum state --or perhaps an appropriate extension of it, or more detailed understanding of it-- manages to pack in it what we perceive as classical data (the results of experiments, or how the quantum systems "decide.") It is my feeling that there are enough clues in the formalism, to the extent that it's been developed today, for these classical data to be carried by the wave function. But the lesson from the impossibility theorems is, perhaps, that we cannot make this connection naively. That the demand that the eigenvalues are defined inside the quantum state is too strong a requirement. This information could be stored in the quantum state through "beables," rather than "observables." Quantities that can never be observed, essentially complex in nature --more general complex operators, rather than Hermitian--, and essentially "internal" to the quantum state. Very much like John Bell once suggested, if I understood his ideas correctly. When you look closely at the quantum formalism, you find that there is an extraordinary freedom that seems to point to a fundamentally unobservable domain: global phase, local phase (gauge ambiguity), indefinition of the measure in the Feynman path integral... The problem is, of course, how do we formulate this "internal domain of the wave function" in terms that can be made into a falsifiable theory? What's clearly not the path to follow, IMO, is denouncing the principles of locality and relativistic causality, as @bangstrom --deeply involved in an internal monologue, AFAICT at this point-- keeps parrotting, rather than making a case for. And the reasons are (1) There's no experimental evidence for it, and (2) There's no suggestion from the formalism that this should be the case. Or/and also perhaps how the information is packed in the quantum state, like eg, in thermodynamics of state variables, cyclically: Sx(Sy,Sz), Sy(Sz,Sx), Sz(Sx,Sy); in such a way that there are no three fundamental variables of spin, but only two complex variables. I've always found fascinating how the mathematics of spin resembles the mathematics of thermodynamic variables.
-
I think it's interesting to try and find analogies that reproduce some of the peculiarities of QM. What I usually feel is that some analogies manage to reproduce one aspect of it, while others are good at reproducing another. But all of them generally fail at reproducing all features completely. Incompatible questions are questions you can't ask at the same time (impossibility of simultaneous interacting measurements) and for which you cannot prepare states perfectly defined in both answers (impossibility of filtering measurements that produce definite values for both.) After you introduced your husband and wife analogy, I started thinking of a similar extension for the analogy corresponding to another, incompatible observable. I was thinking along the terms of: When both of them got married they signed a pre-nup contract, and one of them owns a house. But for some reason the contract was ambiguous as to the ownership of real estate. So until the question is legally settled, it is not defined whether the house belongs to the family of the deceased, or to the surviving one. Something like that. I will take more than one look at your version of the analogy, but for the time being I'll tell you that I was thinking in similar terms. Only with the undefined property being ownership over one object --or the right to use it, if you prefer. I think it gets close to the idea somehow, although the analogy becomes more and more complicated as you try to fit more aspects of actual QM.
-
Exactly. If you measure a particle's spin along a particular direction, that spin is no longer entangled to any other spin in the universe. You have just set up a qubit to 0 or 1, as people in quantum computing say. Well, sure, of course. You could also send electrons and positrons, one after the other. Or whatever other code, or use the frequencies and positions, like we do for a TV set. But then it's not information contained in the spin. It's in other variables. And they would be subject to subluminal speed limits and causality. Like anything else. Is that helpful?
-
If you sit at one place and take spin measurements on a particle (say a photon,) being completely clueless about whether that particle comes from an entangled pair, or triplet, etc., you wouldn't know. There's hardly anything you would be able to say about other parts of the universe it's just disentangled from. One particle is... well, one particle. You measure its spin --after that, it becomes disentangled from whatever it was entangled with before --as @MigL said. Suppose it gives +1 in the direction you set your polariser at. What can you say from that? Practically nothing. +1: That's all your information. Just one piece of data from a measurement doesn't tell you anything much about where it came from. If you take care not to do anything that changes the spin, it will produce +1 again and again. So, sure, you can say something about this photon now. If, OTOH, you measure spins for a stream of particles all identically prepared in the same entangled state, you would see a sequence now. It could go like: +1, +1, -1, +1, -1, +1, -1, -1, -1, +1, +1, -1, +1, +1... So what? What can you tell from that? You can call upon Zeilinger himself, if you wish, to interpret your data. You can tell nothing from that. Not yet. It's just a random sequence of binary code. But, if you can arrange to communicate --by the usual, sub-luminal channels-- with someone far away in the Andromeda galaxy measuring the partner particles making up the identically-entangled pairs, now, and not before, you would be able to tell something, if you're lucky. If you both have chosen the same polarisation direction for your respective polarisers, you would find something funny: They're exactly anti-correlated each and every time. When your particle reads "+1", the other one reads "-1", and viceversa. But if you set your polarisers in a non-parallel way, there's not even the slightest amount of correlation. That's a big wow! on my part. It's strange, weird, seems magic --if you don't understand QM. But still doesn't allow you to send any signals in and of itself. As I said in the other thread, concerning quantum teleportation: https://en.wikipedia.org/wiki/Quantum_teleportation However, and most importantly, even if, after having gone through all that trouble, you find the perfect anti-correlation, your local stream of data (the sequence of +1, +1, -1, +1, -1, +1, -1, -1, -1, +1, +1, -1, +1, +1..., etc.) is still a random, nonsense, totally-garbage noise of +1's and -1's. What do you wanna do with that for the purposes of communication? See my point? Do you want to communicate with the Andromeda galaxy with photon spins somehow coding a message? Fine. Here's one particular way you could go about doing that. You take a sufficient power of 2, eg, 27=128 You can code 128 characters with this. More than enough for all to represent the different characters in the English language, lower case and capitals, plus Arabic numerals, spaces, punctuation, and a bunch of special symbols. It could go like, Space -> 0000000 Dot -> 0000001 a -> 0000010 etc. Now you can prepare your photons to "mean something." It would --it would have to-- look like a pre-determined, precise sequence of zeros and ones. Importantly, you have to filter the sequence so that each photon is +1 (stand-in for 1) or -1 (stand-in for 0) to be precisely at the place it has to be to constitute your message. I think the idea is clear enough at this point. You can't do that with the output of an entangled state. A random string of 0's and 1's is not a message. And it's not, no matter what direction you set your polarisers in. Sending a random sequence is not a message, no matter how non-classically structured these strings of noise are. Even though they are. All my previous comments go without even starting to consider the problem of keeping quantum coherence through interstellar space all the way from here to the Andromeda galaxy, with interstellar dust, asteroid rings, cosmic rays knocking off my photons, etc. I don't envy the engineer whose task was to guarantee something like that.
-
Yes. He really needs to read --with utmost attention-- Einstein's Gedanken on how two distant observers synchronise their clocks. SR is not a nagging theoretical preconception that can be brushed aside for the purposes of doing your thing. It's the theory of how one attaches times and positions to events, and does it consistently. That's why we're beeing such "sticklers" about this. Let's see if he finally understands this, because last time I looked he qualified it as "bickering."
-
Eise also told you how the Clauser experiment is not, while the Aspect experiment is an Alice & Bob SR situation. You really should get your "stuff" together, Bangstrom. I can't say a 100% you're just trolling around, because I must confess I've also considered --like Eise-- possible language barrier, circumstances I may not be aware of, etc. But this is getting ridiculous, and it does sound like you're just trolling around.