joigus

Not really. But you can make it one. I'm sure you've taught a teenager at some point in you life. If you want to share your recollections/conclusions on a new thread I, for one, would be interested.

No. Sometimes infinity appears in a mild form, that can be tamed. That's why we teach those instances to teenagers (eg limits.) Other times it's like you say. Still other times finite problems are every bit as difficult. And quantum superpositions are not superpositions of 'real' and 'imaginary.' What are you on about?

Just another WAG.

I'm OK with that. Every time mathematicians publish a proof, there's a time period during which the jury is still out. Another caveat on terminology though. Mathematically-minded people like to say 'QFT is a functor' --thereby 'functorial.' This is a concept in category theory. People also say 'action is a 'functional' --a function of function that produces a number. Those are very different concepts with very similar terms, so it's necessary to tread carefully.

I think I got a reasoning that recovers the 1/2 factor that @sethoflagos posited from Bernouilli's equation and, by now, I'm totally convinced is right. In the general situation --but still idealised, as we are assuming an infinite wall, and a constant velocity field pointing right in the image, we'd have something like, An ensemble of particles that's equivalent as to momentum --and K.E.-- transfer is, This would give a velocity field and a density that are consistent with the continuity equation iff 1/2 the molecules are going right, and the other 1/2 is going left --but with half the velocity. Otherwise, we wouldn't be getting an overall velocity field going right with velocity v, as 2v-v=v, while v-v=0. So the density \( \rho \) must --on average-- be made up of 1/2 the molecules going right --and eventually hitting the wall--, and the other 1/2 going left --and therefore never hitting it again. Although we still have \( \rho\triangle V=\rho Sv\triangle t \), this gives us twice the molecules that are going to hit the wall within time \( \triangle t \). Therefore, I should have written, \[ \triangle p=\frac{1}{2}v\triangle m \] which gives \( \frac{1}{2}\rho v^{2} \) for the pressure. In the more realistic case, it is certainly true that molecules moving wildly in all kinds of oblique directions would contribute to the --constant-- density, but this is made up for in the simplistic model by assuming that they're not there, and the average leftward motion is totally carried by particles moving perpendicularly to the wall. Note for @Boltzmannbrain on aspects already mention by other members: Newton's equations of motion are valid thoughout, of course. But there are cases in which thinking in terms of momentum transfer is more useful. This is, I think, one of them. Please tell me whether you agree/disagree with this --admittedly-- drastically simplified model.

Here. I didn't remember very well. Mathematicians seem to have proved it's unsolvable, on account of incompleteness theorems: https://www.eurekalert.org/news-releases/490733

Sorry I can't comment much on that. I know next to nothing about Polyakov loops. From what I gather, those are Wilson loops applied to a QFT upon which you've performed a Wick rotation. I suppose they give you topological invariants of the corresponding thermal theory?

I think @studiot knows much more about projective geometry than I do. Also other members who are mathematicians, or much more educated in higher mathematics. The mass gap in YM is considered to be the toughest problem around concerning physics, BTW. Just saying...

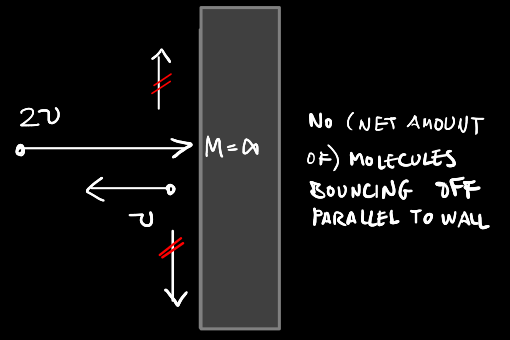
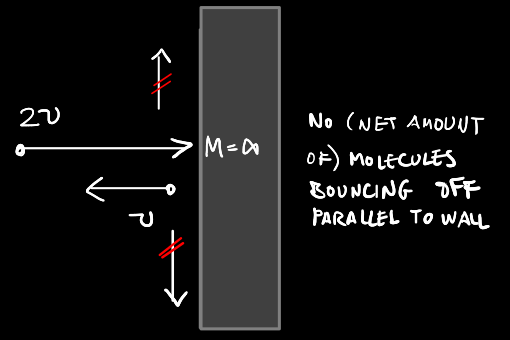
That was I --speaking a la Gandalf. By the way, I still think @swansont's argument is the ticket here. @Lorentz Jr is right though. Any realistic situation will be riddled with turbulence. Still, you can concoct a non-turbulent system for which the energy/momenta analysis is equivalent. Crudely speaking, that's because you can picture all the molecules hitting the wall at speed 2v, and all of them bouncing off perpendicularly (to the wall) at speed -v, the wall absorbing the deficit of kinetic energy, and the flow of particles still being a stationary flow which on average has velocity v towards the wall. Momentum would be conserved, and the continuity equation wouldn't suffer in the least.

Mmmm. Sorry, I didn't see your factor 1/2. I don't think conservation of (kinetic) energy will give you the right answer here. There's no reason to assume collisions are elastic. OTOH, momentum is always conserved at a macroscopic level. That's why I think Swansont's suggestion is the most secure foundation for this kind of reasoning. Does that make sense?

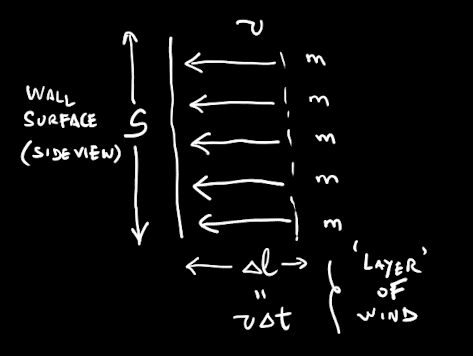
Agreed. You can get Seth's 'hydrodynamic' formula, from Swansont's suggestion. Consider some amount of time \( \triangle t \). With @studiot's suggestion of 1 second, the maths is slightly simplified. This defines a reference layer of wind. \[ \triangle l=v\triangle t \] \[ \triangle V=Sv\triangle t \] Every \( \triangle t \) seconds the corresponding layer of wind will transfer momentum to the wall by an amount, \[ \triangle p=v\triangle m \] where, \[ \triangle m=\rho\triangle V=\rho Sv\triangle t \] And the resulting pressure would be, \[ P=\frac{F}{S}=\frac{v\triangle m}{S\triangle t}=\frac{\rho Sv^{2}\triangle t}{S\triangle t}=\rho v^{2} \] As Studiot pointed out, momentum parallel to the walls is canceled out. While the air molecules bouncing back cannot transfer momentum back to the wind, so to speak, as we're assuming the gust of wind to be constant --it has reached some static regime. I forgot to mention my \( \rho \) is @studiot's d --the constant density.

I see no way in which anybody could disagree with it. And that's not good, I think.

The video certainly makes it looks as if it's the nuclei that are working as forced oscillators. Looking forward to your comments.

OK. So what I see here is: (1) Indeed Dr Lincoln says 'the photon absorbs the atom' at about 5.34. But I think that's just a slip of the tongue. (2) He doesn't mention the amplitudes, nor does he mention the frequencies involved. A forced oscillator responds with an amplitude that depends on the forcing oscillation frequency, the friction coefficient, and the natural frequency of the oscillator. But the frequency that survives, after the transient has died out, is the same as the frequency of the driving force. He omits those aspects, I think, for the sake of simplifying the explanation. He's mainly concerned with what he perceives as ongoing confusion due to flawed arguments on YT and the like. If you treated every single atom in the crystal as dipole, you could in principle calculate, by solving Newton's equation, how much it accelerates. You would need a formula to calculate the additional radiation, which is not easy at all. Of course, none of these details are dealt with in the explanation. And I understand why they aren't.

I think you're still confused as concerns 'fields' in algebra vs 'fields' in physics. Very different things. It's like 'dog' in 'hot dog' vs 'dog' in 'I'm walking my dog.'

What is a centripetal velocity? You mean angular velocity? Of what? Please, pick a scenario and stay with it for as long as you can. Reaction of a plane, Euler forces, now atmospheres... These are very different things. What's next? I don't see a circular argument. More like a Brownian motion.

Excellent idea. Thank you.

Might this be the only time you've specified an event? Even if it's only an impending one?

Oh, I missed that part. Sorry. I've started at about 7.05, as Lorentz Jr & exchemist said that was the juicy bit. Maybe it's worth a thorough look. I'll do that ASAP. This link @Lorentz Jr posted, https://en.wikipedia.org/wiki/Ewald–Oseen_extinction_theorem is worth a look or two. It's pretty much what I was fumbling towards.

Studiot's post already summarised at least part of the approach. At this point I think my explanation has lost interest TBH, because it's not so much one about 'mechanisms' as it is one about quickly and efficiently plugging in what we know, and simplifying the maths. I don't think there's any fundamental disagreement between one and the other, in spite of some sentiments expressed to the contrary. When you consider matter is made up of atoms, it's sometimes more convenient to package properties together in different densities, that's the essence of it. The main idea is that every time you have a material, it will react according to its properties, and those are --in the case at hand-- conductivity, polarisability, and magnetic properties. I'm busy trying to wrap up a quick explanation while simplifying the maths as much as possible, but it's turning out to be harder than it looked. Here's part of the reason: (from https://www.oceanopticsbook.info/view/theory-electromagnetism/level-2/maxwells-equations-matter#:~:text=ρ b %3D − ∇ ⋅ P,ρ f − ∇ ⋅ P .) I think I can do it, but please keep in mind, (1) I realise now that my explanation is not all that interesting --especially considering you're a chemist, and are probably more interested in the molecular mechanism. Also, I've finally watched the video, and it's more than good enough for me. (2) It's going to take some more time. I have to clarify notation, review the maths, and trim the whole thing down to what's of interest to us.

Hey, count me in. @Lorentz Jr is doing the thankless job of trying to see what's inside the cuckoo clock. (1) You never specify events, or are very ambiguous about it. You keep referring to frame-dependent quantities as if they must mean something to a 'super-observer' that's only in your mind. (2) You never specify reference frames, or conflate different frames in one sentence. (3) You systematically ignore, or make no reference, to experimental results which, needless to say, totally confirm SR in each and every instance that's been looked into. In summary, you don't understand SR, nor are you willing to learn about it --or so it seems. It's impossible to follow your logic because there appears to none. None that's worth considering, anyway.

If you mean the concept is that entropy is not conserved, and 'eventually' could mean 'infinitely far ahead in the future,' and that nobody is actually sure whether that will actually happen, among other things due to gravity being exceptional in almost every sense concerning entropy, and being the fundamental mechanism behind the evolution of the universe, I guess you're right. Indeedy!

What potential conservation of entropy? There is no such thing as conservation of entropy. You have a physical system. It has myriads upon myriads of microstates that have all the fine-detail distincions. Then you introduce coarse-grained distinctions, or cells, that include many microstates in them. That's information --of some kind-- for you. Perhaps because you don't know the fine details, perhaps because you don't care, or perhaps both, you don't know what's in the cells. No matter how you create the distinctions, if the system has the possibility to change --it hasn't reached thermal equilibrium yet-- your entropy will increase for the universe as a whole. It will also increase for an isolated system that hasn't reached thermal equilibrium yet. Example: A box, thermally isolated, with rigid walls. You have two different gases and a wall separating them. You remove the separating wall. The gases will mix, the system will reach a common temperature, pressure, volume, chemical composition, etc. All the information that you had stored in your system will have disappeared. Entropy has to do with information in the last analysis. Only when your system has reached thermal equilibrium, your entropy will stay the same. So no, there is no conservation of entropy, potential or factual. Entropy conservation would imply time, in a way, has ceased to exist. That's what people call thermal death of the universe.

Thank you, and no problem.

Like some kind of drag? Yes, that could do the work. I liked exchemist's analogy of the person trying to run on a trampolin too. I have to confess I've become sort of simplistic. And I'm far too fond of the formalism too. I think I understand polarisation well. I plug in the electric displacement, and that modifies the velocity constant. If the medium happened to be inhomogeneous, with regions of higher refraction index and regions of lower one, the explanation based on superposition of waves would be a mess. But you could still depart from the principle of least action and proceed from there. If one is happy with an intuitive explanation, the "drag" argument that you suggest sounds perfect. How natural that is in the mind of a person who wants to understand it crudely, I don't know.