joigus

Maybe this one works for "male" and "female"? \male Undefined control sequence \male \female Undefined control sequence \female DDo I think you don't need environment "displaymath" for that one. Simply: \[ T=\sum_{\begin{array}{c} i_{1},\cdots,i_{n}=1\\ j_{1},\cdots,j_{m}=1 \end{array}}^{d}T_{i_{1}\cdots i_{n}}^{j_{1}\cdots j_{m}}E_{j_{1}\cdots j_{m}}^{i_{1}\cdots i_{n}} \] should work. Let's see: \[ T=\sum_{\begin{array}{c} i_{1},\cdots,i_{n}=1\\ j_{1},\cdots,j_{m}=1 \end{array}}^{d}T_{i_{1}\cdots i_{n}}^{j_{1}\cdots j_{m}}E_{j_{1}\cdots j_{m}}^{i_{1}\cdots i_{n}} \]

Yes, it is. It is exactly what you said. Are you suggesting I'm tinkering with the quoting function, or I'm lying?: It is simply not true that every particle, given enough time, will eventually interact with another particle. Two photons that are being lost beyond the cosmic horizon in opposite directions, eg, will never meet again, or interact in any way. It is false. What you said, you said, and it's false. False, shockingly ignorant statement. Entanglement always occurs as a consequence of local interactions. Particles must be brought together for them to entangle. Here. Simple Google search of "what causes particle entanglement": In the case of parametric down conversion, it's the (non-linear) response of the crystal to a laser at a particular location in the crystal. No. It illustrates the moment when the particles disentangle. You're misquoting here, or just plain lying. Point to me where anybody said that "the ambiguous nature of SR events for different observers can reverse the order of time-like (separated) events." This, most likely, is a new half-digested regurgitation from your mind of what others have actually said. Missing the point again. I will rephrase correctly your gazpacho of words and, with any luck, you will see what you said wrongly: The observation of one quantum property cannot indicate the possible outcome of any other incompatible quantum property. The observation of one quantum property completely determines the possible outcome of the compatible quantum property that's tied to it by a conservation law. And that, my friend, is why realism has no business in explaining quantum mechanics. Never underestimate the value of repetition.

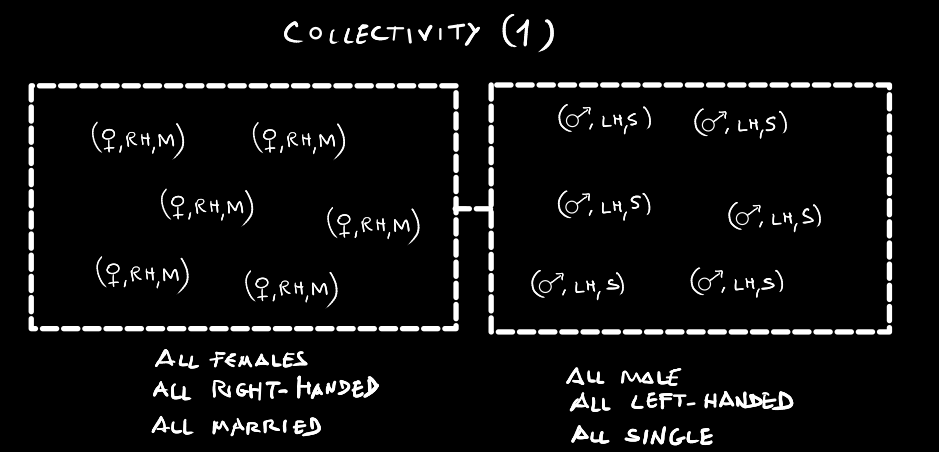
Finally. Here it is. I'm sorry that the explanation is quite lengthy. But I hope it's transparent. In order to explain why non-realism is all that's going on, I will try to work out an example that very much amounts to reverse-engineering Bell's deductive formulation of the contradiction between QM and hidden-variable models. I'm going to do it inductively, instead of deductively, trying to figure out what kind of (realist) collectivities you would have to postulate in order to explain quantum correlations. Here's how you do it. Let's take pairs of astronauts, and two space pods. We pick both astronauts from certain cohorts, arranged is some way or other --we'll see about that in a moment-- so that we may hopefully reproduce the quantum correlations. Let's introduce three basic observables for the astronauts: \( \mathcal{G} \) (gender,) \( \mathcal{H} \) (handedness,) and \( \mathcal{M} \) (marital status.) Let's assume the observables to be sharply dichotomic in their spectrum (possible outcomes of observing each property): Gender: \( \leftarrow \) (female), \( \rightarrow \) (male) Handedness: \( LH \) (left-handed), \( RH \) (right-handed) Marital status: \( M \) (married), \( S \) (single) Let's also assume that these properties are mutually incompatible, in the sense that I am allowed to ask the question, "is the astronaut a married person?" But then I'm not allowed to "experimentally ask" whether it's a woman, or whether it's LH or RH. We must ask one, and only one question. This is meant to crudely replicate the concept of incompatibility in QM. Let's also represent our "hidden internal states" with round brackets. Eg. a female, right-handed, married astronaut would be \( \left(\leftarrow,RH,M\right) \). BTW, this is what's not going to be possible. Einstein's hope to claim these internal states as "real" (elements of reality) was that we perfom the experiments for incompatible properties by exploiting a conservation law, and asking the two incompatible questions in different sub-systems. Eg.: Gender for astronaut (1), and handedness for astronaut (2). Let's represent pairings of experimental outcomes with square brackets: Gender for astronaut (1) and marital status for astronaut (2) would be \( \left[\mathcal{G},\mathcal{M}\right] \), while a possible outcome would be \( \left[\rightarrow,M\right] \), which reads: "Astronaut (1) is a male, and astronaut (2) is married." We can, of course, decide to measure for both astronauts the same property. In our notation, that paired measurement would be represented by, eg, \( \left[\mathcal{H},\mathcal{H}\right] \) (handedness, handedness.) Now we select two astronauts, put one in one space pod, and the other one in the other space pod, at random: We throw a coin to decide. Very important observation: Now we can have the space pods fly in opposite directions, or we can decide to conduct the experiment in the same place. It doesn't matter. Whether the pods are in the same place or light years apart when we do the measurement is not an issue. Quantum computations give the same result no matter what we decide at this point. That's key. Another very important observation: At some point, you've put your finger on a real conundrum, which is what happens after we measure the properties, and the question of how the quantum state is updated. This is known as the "measurement problem," and it's part of the reason why some kind of formal non-locality could be invoked. "Formal," because no measurable consequences can be extracted from it. But that's another story. It's the story of how Copenhagen's interpretation of quantum mechanics cannot be taken but as a useful practical rule. Now, back to our "experiment." I said: For this to be the case, you would have to measure pairs of compatible properties. That is: \[ \left[\mathcal{G},\mathcal{G}\right] \] \[ \left[\mathcal{H},\mathcal{H}\right] \] \[ \left[\mathcal{M},\mathcal{M}\right] \] As is well known, in this case the results are perfectly anticorrelated (but random!!). Examples: \[ \left[\mathcal{G},\mathcal{G}\right]:\left[\rightarrow,\leftarrow\right],\left[\leftarrow,\rightarrow\right],\left[\rightarrow,\leftarrow\right],\left[\leftarrow,\rightarrow\right],\cdots \] \[ \left[\mathcal{M},\mathcal{M}\right]:\left[M,S\right],\left[S,M\right],\left[S,M\right],\left[M,S\right],\cdots \] \[ \left[\mathcal{H},\mathcal{H}\right]:\left[LH,RH\right],\left[RH,LH\right],\left[LH,RH\right],\left[LH,RH\right],\cdots \] If you think about it, in order to get this results alone, and if you insist on the triplet of properties being "real" all along, you would have to pick a cohort like, Or perhaps others, like all \( \left(\leftarrow,LH,S\right) \) in one sub-cohort, and the exact opposites for every property, \( \left(\rightarrow,RH,M\right) \) in the other. There is no other way. It's the assumption of realism that leaves you no other way out. On the other hand, I also said: And here's how. The totally uncorrelated outcomes for incompatible pairings are like, \[ \left[\mathcal{G},\mathcal{M}\right]:\left[\rightarrow,M\right],\left[\leftarrow,M\right],\left[\rightarrow,S\right],\left[\leftarrow,S\right] \] \[ \left[\mathcal{M},\mathcal{G}\right]:\left[M,\rightarrow\right],\left[M,\leftarrow\right],\left[S,\rightarrow\right],\left[S,\leftarrow\right] \] \[ \left[\mathcal{M},\mathcal{H}\right]:\left[M,LH\right],\left[M,RH\right],\left[S,LH\right],\left[S,RH\right] \] \[ \left[\mathcal{H},\mathcal{M}\right]:\left[LH,M\right],\left[RH,M\right],\left[LH,S\right],\left[RH,S\right] \] \[ \left[\mathcal{H},\mathcal{G}\right]:\left[LH,\leftarrow\right],\left[RH,\rightarrow\right],\left[LH,\leftarrow\right],\left[\rightarrow,RH\right] \] \[ \left[\mathcal{G},\mathcal{H}\right]:\left[\leftarrow,LH\right],\left[\rightarrow,RH\right],\left[\leftarrow,LH\right],\left[\rightarrow,RH\right] \] All equally likely. Now, if you think about it, in order to get these results, and you insist on having them from statistical cohorts or picking from subcohorts that hold these properties all along, as real attributes, you have no other way but doing it from, IOW, there is no way that you can obtain both statistical behaviours at the same time with any reasonable assumption of cohorts that hold these properties as real. That's my reverse-engineering of Bell's theorem --or its violation by QM, to be more precise-- for you. Note: Sorry, the usual symbols for male and female don't work here, so I've edited the Latex with \( \leftarrow \) for "female" and \( \rightarrow \) for male. (Except in the pictures.)

Excellent arguments here. I would like to add another one of my own. The contention that, however plausible it may be, is not the same as the contention that certain accidental (visual) projections of stellar objects that are many light years apart from each other, by their sheer apparent position in the sky on this planet with respect to closer stellar bodies --Moon, Mars, etc.--, somehow determine our destinies. Swansont has pointed out how information is hopelessly scrambled by thermalisation. Exchemist and MigL have pointed out limitations imposed by quantum mechanics. Bufofrog has pointed out the fundamental obstruction of relativistic causality. The Vat has pointed out how devoid of predictive power such connections are. I just want to point out that the assumptions of astrology and the observation that everything may ultimately be interconected, therefore maybe everything is affected by everything else, are quite different in and of themselves. The first is pure nonsense or extremely implausible at the very least; the second might be true if, in a remote past, everything was causally connected somehow. But, even if true, it would be pretty sterile in terms of prediction and retrodiction. Truisms and reasonable "possibilisms" are not very useful to make solid science. Suppose you tell a paleantropologist: Somewhere out there must be the first rock that a hominid chipped into a stone tool. Go find it! What hope do we have of finding such an object? How would we know for sure it's the first such object? Suppose we find it. What particular aspect --in this case, of human evolution-- would it illuminate?

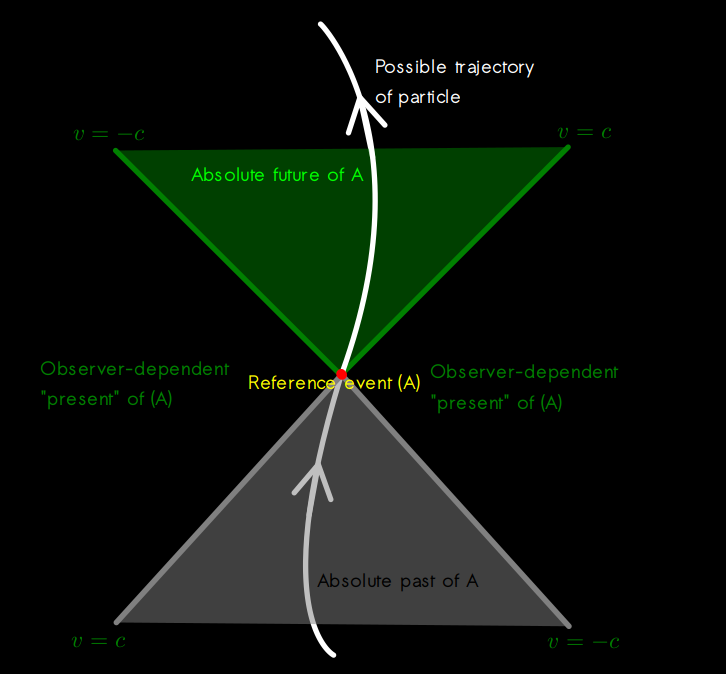
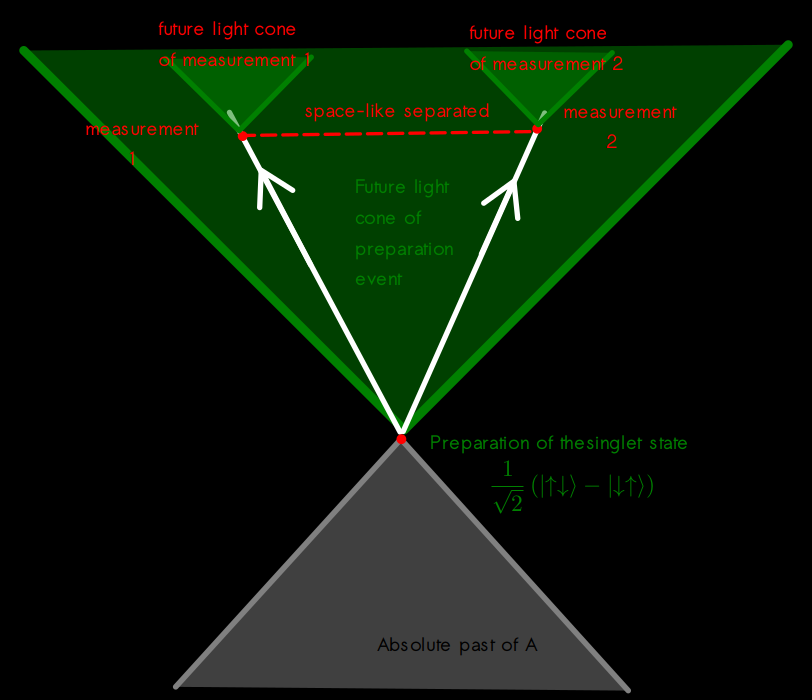
No. Two photons parting away from each other will never meet. Also, light cones refer to events, not to particles. Read @Eise's comments above, if mine seem obscure to you. No, there's no "remarkable exception." Again, you ignored something I said later. I made a significant addition because I fell in the trap of your ambiguous language of referring to "a light cone" without specifying the generating event, which of course, is meaningless: Here's a drawing of a generic light cone, with a particle trajectory for the purposes of illustrating its role in general. And here's a drawing of the situation in the EPR experiment, with all the light cones that are relevant to it: So, as you can see, every event "carries" its own light cone. Measurement 1 is outside of measurement 2's light cone, and conversely, measurement 2 is outside of measurement 1's light cone; while both are well within the antecedent preparation of the quantum state's big whopping light cone. What's wrong is that, for space-like separated events, time ordering is ambiguous. So the thing that's "happening" before or after, as the case may be, has to be completely ineffectual (for all intents and purposes, just a re-definition of the wave function,) and only in your mind, really. Eise has just explained how the ordering is ambiguous. If it had any consequences --measurable ones, interactions, etc.-- it would be very bad for SR. It doesn't happen.

Yeah, yeah... Blah, blah. Every time you're caught in an embarrassing lack of understanding of the basics of this problem, you choose not to answer and keep blowing smoke in a different direction. Do you or do you not understand the role that the light cone plays in the discussion of causality? This is, of course, a rethorical question, as it's pretty obvious you do not: ⁉️ ⁉️ (my emphasis.) For two arbitrary events, A and B, A can be in the future light cone of B, A can be in the past light cone of B, or A and B can be space-like separated --ie. either one of them is outside the overall light cone of the other. Space-like separated events are never, --repeat, never-- on the same light cone. Events in the same light cone are causally connected. It is for events outside their respective light cones that any discussion of non-locality would make any sense. You are shockingly ignorant of the concept of causality, and of many other physical concepts. Do some explaining and self-correcting, please, because last time you said something about this, you got it completely backwards. And stop blowing smoke. Bad as it is, ignorance is not your problem. Your problem is you think you actually understand something, and are incapable of acknowledging your ignorance. Your problem is the --highly intellectually toxic-- combination of hubris and ignorance. Another possibility is that two space-like separated events are both on the same (future) light cone of a previous event thus including both in the absolute future of such antecedent event. Or both are on the same (past) light cone of a subsequent event, thus including both in the absolute past of such subsequent event. None of these qualifications is in your language. You are either sloppy, or deliberately ambiguous, or both.

You're probably right, but that's the last thing on my mind, as concerns this "debate."

No. It is simply not true that every particle is within the absolute future light cone of another. This proves an absolute ignorance of the principles of special relativity. You know nothing about SR, that's clear enough for everybody here. When the interval between two particles (instants in their respective histories, viewed as events) is of time-like character, then one is in the future light cone of the other, and the character of time ordering between both is observer-independent. When the interval between such two events is spacelike, on the other hand, the time ordering between them is observer-dependent. Of course there is a difference between entanglement and classical interactions. Do I have to go back to square one to explain it to you again? This is the kind of babbling nonsense I have to put up with: Particles are neither space-like or time-like separated. Events are. Local or not is not an attribute of particles. It's an attribute of interactions and/or evolution of the state. When two events are on the same light cone, they are causally connected. Can you get anything, anything!!! right??? Just one little elementary thing. Can you just get one little elementary factoid of SR right?

Yeah, sure. You're waiting. It takes half a minute to dismiss other people's careful arguments with no arguments of your own. But it takes a bit longer to prepare a carefully-thought argument. See my point? With this degree of carelessness it's gonna be hard. When one event is within the absolute future light-cone of another, you don't need to invoke non-locality/violation of relativistic causality to explain it. Maybe thowing a stone would suffice. It's with spacelike-separated events that you do. Do we have to go to the basics of SR every time you say something?

Overlapping symbols test: \mathclap{\fullmoon}\fullmoon \[ \mathclap{\fullmoon}\fullmoon \] Pitty.

Just for the record, I don't see any derivation either. Mathematical abstractions (fields, particles, manifolds) are just constructs to be constantly revised and possibly reformulated. And the argument "how can a particle read our mind" is one of the most bizarre arguments I've ever met.

Again??? No room for speculation when something is obvious. No problem at all in obtaining classical systems with random variables that are perfectly anti-correlated. No need for causation at a distance to explain the correlations. You put, say, the single left-handed woman in one space pod and the married right-handed man in the other. You throw a coin to decide who goes where. You can have as many random, compatible, anti-correlated properties as you want for boots, coins, umbrellas, dice, gloves, armadillos or astronauts. No problem at all in obtaining classical systems with random variables that are perfectly non-correlated. No need for causation at a distance to explain any non-correlations. You put the ambidextrous professor of Russian Literature in one space pod, and the left-handed Vegas hooker in the other. What you can't get with classical systems is random variables that are perfectly anti-correlated for certain pairings of observables, while perfectly non-correlated for other pairings of observables. What you can't get with classical systems is both at the same time. But again, no need for causation at a distance to explain the overall correlations. The quantum state has all you need, and it was prepared at one small region of space, and at one time. I'm working on an example that's so transparent that even you will have to agree with it. Let's see what happens.

(my emphasis) You suggested them: Cosmic rays don't come from the Sun. They come from every direction in the sky. They affect the conductivity of the atmosphere, but do not explain separation of charges. And this is not your question.

This doesn't make any sense. They have different dimensions, scaling properties, and dependence with distance and orientation. Curie's law doesn't apply here. AFAIK, higher conductivity in the upper layers of the atmosphere is to do with ionisation due to cosmic rays. In the thermosphere there's actually a temperature inversion, so it's not colder, but warmer than adjacent layers. Magnetic fields are not responsible for separation of charges to significant distances. Electric fields are. Friction is probably involved too. Stop hijacking/soapboxing, please. I will be quiet now, because I want to learn something. I suggest you do the same.

You missed my point. You talk about particles as obvious pieces of input from sensory experience. But somehow you mistrust the concept of fields, because they don't implement correctly what these particles do. What you don't seem to understand is that both, particles and fields, are conceptualisations. Neither is more closely-related to sensory input than the other. Both are theories. That was my point. And, as Studiot said, it was Faraday who introduced the concept of a field.

Apparently this advanced civilisation will spare no effort in telling the universe about the big news: Six is next to five. Exactly what I noticed: low intensity-peak-low intensity.

Not exactly. The correct statement is: If momentum is zeroed-in with a finite precision of, say, \( \Delta p_x \), x-position can be zeroed-in with finite precision no better than that given by HUP. That is \( \triangle p_{x}\geq\frac{\hbar}{2\triangle x} \). When \( \triangle p_{x}=\frac{\hbar}{2\triangle x} \), you get "minimal packets." http://www.embd.be/quantummechanics/minimum_uncertainty_wave_packet.html But even in this desirable situation, you cannot get perfectly defined momentum. And worse: even though packets left to free evolution tend to get "plane-wave" profile, and thereby more and more defined momentum, their position precision spreads as they go, like this. So the situation is far from being as clean as Einstein would have wanted it to be. I'm sure that's the reason behind the fact that David Bohm took the whole discussion to spin. In that case, you can devise a situation in which an observable is constructed by adding up two "statistically disperse" variables, while the sum of both is "statistically dispersionless." This situation does not equate with non-locality, as it's just a matter of waves of different frequencies (and wave numbers) having different phase velocities, which becomes transparent when you do their Fourier analysis. So no, this is not non-locality. Waves --that are not solitons-- on the surface of the water, also suffer the same kind of dispersion.

Think about it. You must provide heat to make the pressure constant during an expansion. Hm. There's something more to it. I can't read the image very well.. Sorry, I misread. It's a chemical reaction. OK. I think I see what the problem is. The criterion that you use is consistent with \( w = -P\Delta V \), right? Not with \( w = +P\Delta V \) Some people write \( \Delta U=q-w \), and other people prefer \( \Delta U=q+w \), but when expressed in terms of P, V, in the 1st principle, it must always be, \( \delta U = q-p\Delta V \), because if it's an expansion, the contribution to the internal energy must be negative. That's what's written in stone. Maybe you got confused with a sign criterion you saw somewhere else? Sorry for the initial confusion. Was that helpful?

No. You can hand someone an object that attracts another object. You then take measurements, see how it depends on distance, amounts of matter, velocity, etc., start thinking in mathematical terms to parametrise that, express the patterns as mathematical relations, and finally come up with the idea of a field. Then you test your theory. You don't seem to realise that even the notion of a particle underlies a theory. Before the first Greek natural philosophers (proto-scientists) nobody thought seriously of particles. Some theory said that everything was some kind of continuum, made up of a mixture of water, earth, air, and fire. Nothing "obvious" about the theory that things are made up of particles. And when you get to radiation, even that idea fails. You need fields. And when you get to quantum phenomena, even that idea fails. You need field quanta. And so on. Taking as starting point that particles are a given shows very poor reasoning, as well as knowledge of the history of science.

Sorry, I meant: because all the other alternatives that were coded in the quantum superposition in some sense disappear. I'm sure most people understood that. Funny summary. Funny too, but in the other sense. It is my impression that if you sit long enough and think about Bell's analysis, you're bound to eventually find yet another possible loophole for some kind of "weak realism", or another. Maybe some kind of "emergent realism," or "fiduciary realism," as I tend to see Bell's beables, "superdeterminism," "hypercontextuality." I'm expecting new fancy concepts, most of them probably not very compelling, and having to face the inevitable sharp edge of Ockam's razor. The inspiring mood being: Try to find a way in which you can weaken the reality hypothesis, and you can find a way out. I was in the middle of writing this when @MigL's comment popped up, very much in that direction:

Sorry. Omission: the later one is in the future light cone of the previous one. And that is agreed upon by all observers, according to SR.

Crudely speaking, a theory is local when you can define quantities point-by-point as densities of something (energy, probability, angular momentum, charge, etc., per unit volume), then define current densities from them: the corresponding quantity (energy, probability, angular momentum, charge, etc., per unit surface, and per unit time) that escapes out of that volume through the boundary. For local theories, every quantity that is conserved, in order to leave the volume, must do so going through the surface. In other words, all these conserved quantities satisfy a local conservation law, which reads, rate of change of quantity Q within the volume V = -(flux of current density of Q through surface S) where S is the boundary of V, but otherwise S and V are arbitrary, and Q is any of these conserved quantities. All quantum theories are local in this sense. But the tricky thing is that all these densities become probability densities when quantum mechanics operates at the bottom of it. What people (sometimes, quite loosely, quite sloppily) call "quantum non-locality) is not that. Quantum theories allow you to prepare states that have no definite value of these locally-conserved quantum numbers Q, and then measure their value at the boundary. So you force the quantum state to "decide" (select, einselect) what particular value of the quantity Q it --for lack of a better word-- "encapsulates." You can do pairs of measurements for space-like separated events (so no light ray can join them) or for time-like separated events (so the time ordering between the events is observer-independent: the later one is in the light cone of the previous one). That really doesn't make that much of a difference. And it doesn't because all the alternatives that were coded in the quantum superposition in some sense disappear. Do they go to different branches of existence, no longer connected to the branch we see? Gell-Mann/Hartle style Do they escape away in the form of empty waves, never to be found again? á la Bohm Do they immediately disappear from existence, as the Copenhagen interpretation tells us? Nobody knows. Only theorists really worry about this. And cosmologists, both experimentalists and theorists. None of these possibilities affords any way of exploiting non-local effects because they have no non-local consequences. I could go into more detail about why that is, but suffice it to say that the same flow of probability density for V volumes and their S boundaries is satisfied. Only with a sharply defined value for Q now. And the state, as you already know, is always random in other quantities (those incompatible with Q.) There is logic in there of the type you use and I think you could critique it. I noticed studiot so maybe he can tell if this is worth a damn, too. Thank you. I'll take a look ASAP. Thanks!

Aha!!! +1. Good. You really want to understand this. I've found what's confusing you. The reason is this: This doesn't happen if you don't re-entangle the boxes. If you open the box a second time, or a third time (without bringing the sub-systems together again!) it will give again, and again LH. And again, and again... Unless some further interaction flips the spin or makes it precess, etc. But then, the spins never become correlated again. Or... If, on the other hand, as you say, you make them "somehow" entangled again, you get them back down to a singlet, and re-start the process, you do need to bring the particles together again. This "make them interact again" is what you say yourself (I repeat): Don't dwell on the confusion: They are always random, always! What's unmistakably quantum is not the fact the they are anticorrelated (we can reproduce that classically: boots, gloves, coins...), not even that they are random (we can reproduce that classically too, by introducing stochastic terms in the evolution equations), but the nature of the correlations that comes from non-commutativity. That, and only that, you cannot reproduce any other classical way. I repeat: If you want to re-entangle them again, you must bring them together again. See how (obviously, I would say!) it is totally local? The postulate of projection is what introduces irreversibility in the world by hand, by an ad hoc assumption. What I've just told you is completely contemplated by the projection postulate: https://en.wikipedia.org/wiki/Mathematical_formulation_of_quantum_mechanics#Effect_of_measurement_on_the_state IOW, immediately after a measurement, the state is an eigenstate of the observable you've just measured, so it gives you the same value with a 100% probability. When you project a projection, it gives you the same projection. That's the definition of a projection. The problem is, of course, that we cannot make this rule (that works perfectly in every other sense) comply with the Schrödinger equation. That's the ultimate reason why Zeilinger is inevitably led to say --in the reference you provided, And that's because there's no agreement, really, as to what happens after the measurement. Particles that become entangled need to do so by means of local interactions. If you study field theory, this becomes obvious. That's why all field theorists, Weinberg, Salam, Gell-Mann, 't Hooft, etc., have always been so little impressed by these claims of non-locality.

More comments on Dance of the Photons (my emphasis in boldface throughout): Zeilinger on how Bell's theorem is not the weirdest theorem in the world: I said: Zeilinger on standalone realism itself being at stake in the whole question: But QM already takes care of that => No-hidden-variables for spin, according to the theorems. In this particular connection, I said, Therefore, QM violates classical logic. Period. Zeilinger about how the argument of locality does not play a role in the Kochen-Specker theorem: and I also said, There are more points coming, but for the time being, suffice this to prove that Zeilinger's view is pretty much overlapping, at the very least, with what I've been saying here, and that you haven't the faintest idea of what you're talking about. Now, I hadn't read Zeilinger's book, and I'm very grateful to @Eise for facilitating me the reading of the most significant passages of the book. It's not very difficult for me to "read his mind," as it were, because I've been thinking, reading, and calculating about these topics very seriously for 40 years. I'm not reading anything I didn't know. I hadn't read about superdeterminism or thought about it in any length, because I've never thought it was a serious alternative. Now I'm sure Anton Zeilinger doesn't support it either --thank you, Eise. Now you tell me where I --and most other knowledgeable members-- have misunderstood quantum mechanics, @bangstrom. And please answer Swansont's question once and for all or, with all due respect, "collapse" into the mute state for all that concerns this thread, unless it is for the purpose of stating your thoughtful disclaimers, which I'm sure everyone would accept immediately.

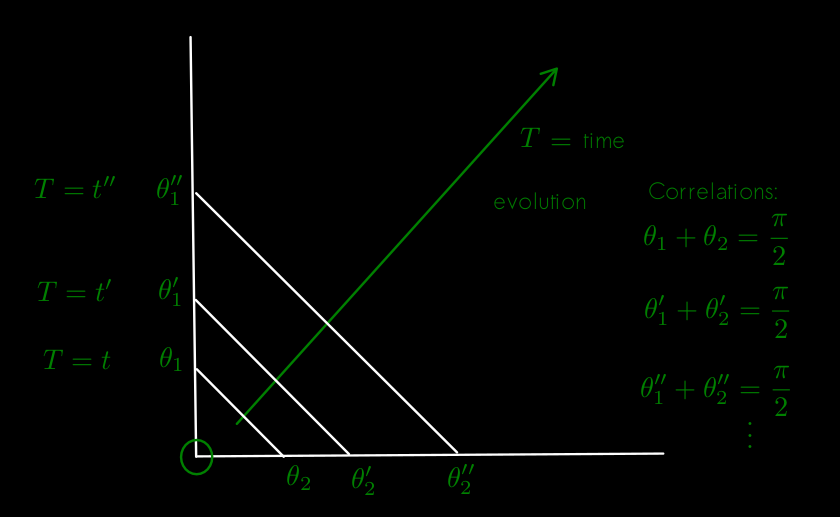
@studiot is not talking about the book he referred to before. He is now making a new argument, designed to help you understand a point very similar to one I presented before: The anticorrelations are built into the state, very much like the Pythagorean theorem is built into the relations of a right triangle, for example --a similar example to the one he is proposing. He is proposing that infinitely many possible values of an angle can be associated to a given value of a trigonometric function. And that should be no surprise, nor it implies a "spooky action between angles." Nor should it be any surprise that the two non-right angles of a right triangle correlate to \( \vartheta_1 + \vartheta_2 = \pi / 2 \). Continuing on my example of the right triangle ("the speed at which the Pythagorean theorem is true is infinity"), but inspired by Studiot's example of the angles: You can take as analogues of quantum evolution the right triangles getting bigger and bigger; the analogue of the correlation, the fact that they add up to \( \pi/2 \), and the analogue of being a singlet state (scalar representation of the rotation group), the fact that the triangles evolve while keeping the geometric ratios (analogue of unitary quantum evolution as well.)