joigus

Again??? No room for speculation when something is obvious. No problem at all in obtaining classical systems with random variables that are perfectly anti-correlated. No need for causation at a distance to explain the correlations. You put, say, the single left-handed woman in one space pod and the married right-handed man in the other. You throw a coin to decide who goes where. You can have as many random, compatible, anti-correlated properties as you want for boots, coins, umbrellas, dice, gloves, armadillos or astronauts. No problem at all in obtaining classical systems with random variables that are perfectly non-correlated. No need for causation at a distance to explain any non-correlations. You put the ambidextrous professor of Russian Literature in one space pod, and the left-handed Vegas hooker in the other. What you can't get with classical systems is random variables that are perfectly anti-correlated for certain pairings of observables, while perfectly non-correlated for other pairings of observables. What you can't get with classical systems is both at the same time. But again, no need for causation at a distance to explain the overall correlations. The quantum state has all you need, and it was prepared at one small region of space, and at one time. I'm working on an example that's so transparent that even you will have to agree with it. Let's see what happens.

(my emphasis) You suggested them: Cosmic rays don't come from the Sun. They come from every direction in the sky. They affect the conductivity of the atmosphere, but do not explain separation of charges. And this is not your question.

This doesn't make any sense. They have different dimensions, scaling properties, and dependence with distance and orientation. Curie's law doesn't apply here. AFAIK, higher conductivity in the upper layers of the atmosphere is to do with ionisation due to cosmic rays. In the thermosphere there's actually a temperature inversion, so it's not colder, but warmer than adjacent layers. Magnetic fields are not responsible for separation of charges to significant distances. Electric fields are. Friction is probably involved too. Stop hijacking/soapboxing, please. I will be quiet now, because I want to learn something. I suggest you do the same.

You missed my point. You talk about particles as obvious pieces of input from sensory experience. But somehow you mistrust the concept of fields, because they don't implement correctly what these particles do. What you don't seem to understand is that both, particles and fields, are conceptualisations. Neither is more closely-related to sensory input than the other. Both are theories. That was my point. And, as Studiot said, it was Faraday who introduced the concept of a field.

Apparently this advanced civilisation will spare no effort in telling the universe about the big news: Six is next to five. Exactly what I noticed: low intensity-peak-low intensity.

Not exactly. The correct statement is: If momentum is zeroed-in with a finite precision of, say, \( \Delta p_x \), x-position can be zeroed-in with finite precision no better than that given by HUP. That is \( \triangle p_{x}\geq\frac{\hbar}{2\triangle x} \). When \( \triangle p_{x}=\frac{\hbar}{2\triangle x} \), you get "minimal packets." http://www.embd.be/quantummechanics/minimum_uncertainty_wave_packet.html But even in this desirable situation, you cannot get perfectly defined momentum. And worse: even though packets left to free evolution tend to get "plane-wave" profile, and thereby more and more defined momentum, their position precision spreads as they go, like this. So the situation is far from being as clean as Einstein would have wanted it to be. I'm sure that's the reason behind the fact that David Bohm took the whole discussion to spin. In that case, you can devise a situation in which an observable is constructed by adding up two "statistically disperse" variables, while the sum of both is "statistically dispersionless." This situation does not equate with non-locality, as it's just a matter of waves of different frequencies (and wave numbers) having different phase velocities, which becomes transparent when you do their Fourier analysis. So no, this is not non-locality. Waves --that are not solitons-- on the surface of the water, also suffer the same kind of dispersion.

Think about it. You must provide heat to make the pressure constant during an expansion. Hm. There's something more to it. I can't read the image very well.. Sorry, I misread. It's a chemical reaction. OK. I think I see what the problem is. The criterion that you use is consistent with \( w = -P\Delta V \), right? Not with \( w = +P\Delta V \) Some people write \( \Delta U=q-w \), and other people prefer \( \Delta U=q+w \), but when expressed in terms of P, V, in the 1st principle, it must always be, \( \delta U = q-p\Delta V \), because if it's an expansion, the contribution to the internal energy must be negative. That's what's written in stone. Maybe you got confused with a sign criterion you saw somewhere else? Sorry for the initial confusion. Was that helpful?

No. You can hand someone an object that attracts another object. You then take measurements, see how it depends on distance, amounts of matter, velocity, etc., start thinking in mathematical terms to parametrise that, express the patterns as mathematical relations, and finally come up with the idea of a field. Then you test your theory. You don't seem to realise that even the notion of a particle underlies a theory. Before the first Greek natural philosophers (proto-scientists) nobody thought seriously of particles. Some theory said that everything was some kind of continuum, made up of a mixture of water, earth, air, and fire. Nothing "obvious" about the theory that things are made up of particles. And when you get to radiation, even that idea fails. You need fields. And when you get to quantum phenomena, even that idea fails. You need field quanta. And so on. Taking as starting point that particles are a given shows very poor reasoning, as well as knowledge of the history of science.

Sorry, I meant: because all the other alternatives that were coded in the quantum superposition in some sense disappear. I'm sure most people understood that. Funny summary. Funny too, but in the other sense. It is my impression that if you sit long enough and think about Bell's analysis, you're bound to eventually find yet another possible loophole for some kind of "weak realism", or another. Maybe some kind of "emergent realism," or "fiduciary realism," as I tend to see Bell's beables, "superdeterminism," "hypercontextuality." I'm expecting new fancy concepts, most of them probably not very compelling, and having to face the inevitable sharp edge of Ockam's razor. The inspiring mood being: Try to find a way in which you can weaken the reality hypothesis, and you can find a way out. I was in the middle of writing this when @MigL's comment popped up, very much in that direction:

Sorry. Omission: the later one is in the future light cone of the previous one. And that is agreed upon by all observers, according to SR.

Crudely speaking, a theory is local when you can define quantities point-by-point as densities of something (energy, probability, angular momentum, charge, etc., per unit volume), then define current densities from them: the corresponding quantity (energy, probability, angular momentum, charge, etc., per unit surface, and per unit time) that escapes out of that volume through the boundary. For local theories, every quantity that is conserved, in order to leave the volume, must do so going through the surface. In other words, all these conserved quantities satisfy a local conservation law, which reads, rate of change of quantity Q within the volume V = -(flux of current density of Q through surface S) where S is the boundary of V, but otherwise S and V are arbitrary, and Q is any of these conserved quantities. All quantum theories are local in this sense. But the tricky thing is that all these densities become probability densities when quantum mechanics operates at the bottom of it. What people (sometimes, quite loosely, quite sloppily) call "quantum non-locality) is not that. Quantum theories allow you to prepare states that have no definite value of these locally-conserved quantum numbers Q, and then measure their value at the boundary. So you force the quantum state to "decide" (select, einselect) what particular value of the quantity Q it --for lack of a better word-- "encapsulates." You can do pairs of measurements for space-like separated events (so no light ray can join them) or for time-like separated events (so the time ordering between the events is observer-independent: the later one is in the light cone of the previous one). That really doesn't make that much of a difference. And it doesn't because all the alternatives that were coded in the quantum superposition in some sense disappear. Do they go to different branches of existence, no longer connected to the branch we see? Gell-Mann/Hartle style Do they escape away in the form of empty waves, never to be found again? á la Bohm Do they immediately disappear from existence, as the Copenhagen interpretation tells us? Nobody knows. Only theorists really worry about this. And cosmologists, both experimentalists and theorists. None of these possibilities affords any way of exploiting non-local effects because they have no non-local consequences. I could go into more detail about why that is, but suffice it to say that the same flow of probability density for V volumes and their S boundaries is satisfied. Only with a sharply defined value for Q now. And the state, as you already know, is always random in other quantities (those incompatible with Q.) There is logic in there of the type you use and I think you could critique it. I noticed studiot so maybe he can tell if this is worth a damn, too. Thank you. I'll take a look ASAP. Thanks!

Aha!!! +1. Good. You really want to understand this. I've found what's confusing you. The reason is this: This doesn't happen if you don't re-entangle the boxes. If you open the box a second time, or a third time (without bringing the sub-systems together again!) it will give again, and again LH. And again, and again... Unless some further interaction flips the spin or makes it precess, etc. But then, the spins never become correlated again. Or... If, on the other hand, as you say, you make them "somehow" entangled again, you get them back down to a singlet, and re-start the process, you do need to bring the particles together again. This "make them interact again" is what you say yourself (I repeat): Don't dwell on the confusion: They are always random, always! What's unmistakably quantum is not the fact the they are anticorrelated (we can reproduce that classically: boots, gloves, coins...), not even that they are random (we can reproduce that classically too, by introducing stochastic terms in the evolution equations), but the nature of the correlations that comes from non-commutativity. That, and only that, you cannot reproduce any other classical way. I repeat: If you want to re-entangle them again, you must bring them together again. See how (obviously, I would say!) it is totally local? The postulate of projection is what introduces irreversibility in the world by hand, by an ad hoc assumption. What I've just told you is completely contemplated by the projection postulate: https://en.wikipedia.org/wiki/Mathematical_formulation_of_quantum_mechanics#Effect_of_measurement_on_the_state IOW, immediately after a measurement, the state is an eigenstate of the observable you've just measured, so it gives you the same value with a 100% probability. When you project a projection, it gives you the same projection. That's the definition of a projection. The problem is, of course, that we cannot make this rule (that works perfectly in every other sense) comply with the Schrödinger equation. That's the ultimate reason why Zeilinger is inevitably led to say --in the reference you provided, And that's because there's no agreement, really, as to what happens after the measurement. Particles that become entangled need to do so by means of local interactions. If you study field theory, this becomes obvious. That's why all field theorists, Weinberg, Salam, Gell-Mann, 't Hooft, etc., have always been so little impressed by these claims of non-locality.

More comments on Dance of the Photons (my emphasis in boldface throughout): Zeilinger on how Bell's theorem is not the weirdest theorem in the world: I said: Zeilinger on standalone realism itself being at stake in the whole question: But QM already takes care of that => No-hidden-variables for spin, according to the theorems. In this particular connection, I said, Therefore, QM violates classical logic. Period. Zeilinger about how the argument of locality does not play a role in the Kochen-Specker theorem: and I also said, There are more points coming, but for the time being, suffice this to prove that Zeilinger's view is pretty much overlapping, at the very least, with what I've been saying here, and that you haven't the faintest idea of what you're talking about. Now, I hadn't read Zeilinger's book, and I'm very grateful to @Eise for facilitating me the reading of the most significant passages of the book. It's not very difficult for me to "read his mind," as it were, because I've been thinking, reading, and calculating about these topics very seriously for 40 years. I'm not reading anything I didn't know. I hadn't read about superdeterminism or thought about it in any length, because I've never thought it was a serious alternative. Now I'm sure Anton Zeilinger doesn't support it either --thank you, Eise. Now you tell me where I --and most other knowledgeable members-- have misunderstood quantum mechanics, @bangstrom. And please answer Swansont's question once and for all or, with all due respect, "collapse" into the mute state for all that concerns this thread, unless it is for the purpose of stating your thoughtful disclaimers, which I'm sure everyone would accept immediately.

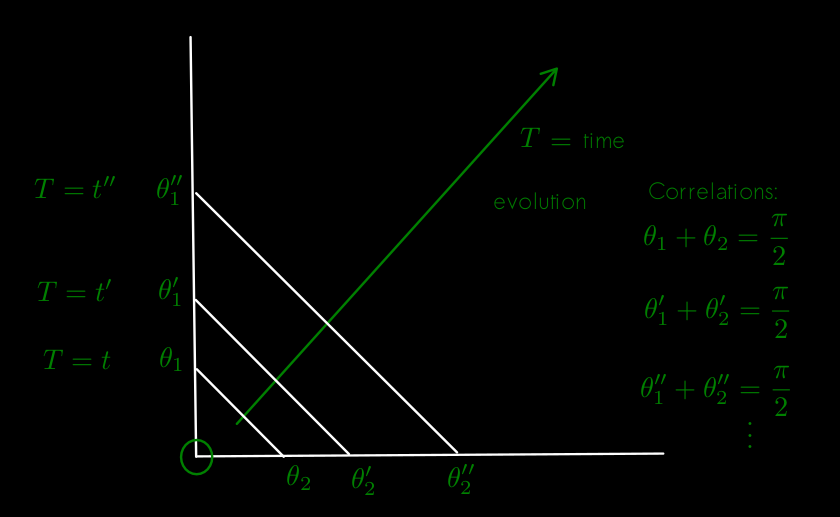
@studiot is not talking about the book he referred to before. He is now making a new argument, designed to help you understand a point very similar to one I presented before: The anticorrelations are built into the state, very much like the Pythagorean theorem is built into the relations of a right triangle, for example --a similar example to the one he is proposing. He is proposing that infinitely many possible values of an angle can be associated to a given value of a trigonometric function. And that should be no surprise, nor it implies a "spooky action between angles." Nor should it be any surprise that the two non-right angles of a right triangle correlate to \( \vartheta_1 + \vartheta_2 = \pi / 2 \). Continuing on my example of the right triangle ("the speed at which the Pythagorean theorem is true is infinity"), but inspired by Studiot's example of the angles: You can take as analogues of quantum evolution the right triangles getting bigger and bigger; the analogue of the correlation, the fact that they add up to \( \pi/2 \), and the analogue of being a singlet state (scalar representation of the rotation group), the fact that the triangles evolve while keeping the geometric ratios (analogue of unitary quantum evolution as well.)

Good point. +1 I've come to a point that I even accept the possibility that not only aspects of reality --sensory input organised by patterns-- could be empty of theoretical constructs as conceptual stand-ins for them, but also some theoretical constructs --especially mathematical ones, but not necessarily just those-- could have no sensory-input counterpart for them. My hope for this possible fly in the ointment of our intellectual satisfaction is that the map could be completed with different patches, very much in the way that cartographers map geographical reality with different patches, and consistency rules for leaping from one to another. A map that faithfully represents regions around the equator, presents major distorsions of Antarctica.

Yes, exactly. While not impossible to conceive, thinking that photons emitted 3 bya by remote quasars somehow code the decisions that primates will take here and now on a particularly rainy day in Vienna at, say, 8:00 AM, is next-to-inconceivable. That the information be so intimately interwoven as to produce this next-to-hallucinogenic coincidental effect is something I don't want to even start to consider. I think the solution to the perplexing results of the quantum theory of measurement are better tackled by some kind of "fiduciary internal determinism." Something very much in the vein of what John Bell proposed with his beable idea. It would involve the idea that a choice of wave function does not determine everything. Infinitely many gauge descriptions would hide the "hidden variables." The catch is: Hidden variables are hidden forever, they never show up completely. They simply can't be seen, ever. There's a logical --and experimental-- fundamental obstruction. I think that's the way out for the problem of measurement, and I think that's the natural logical continuation of John Bell's musings. But that's probably the topic for another thread. That seems to be the case. I cannot wait for her to give up on that, because she is very much the conscience of theoretical physics today.

Sure. I'm sure most everything can be approached by algorithms. The missing part here would be the rotation properties of vector fields, but I'm sure that can be done too. That you're confusing the map for the territory. A map of the world is not the world.

An example is worth a thousand rules. Can you give one?

No. And @studiot is giving you the answer: A rock is made of something. A mathematical object doesn't have to be, because it's defined by logic. It's not made of any ingredients.

Thanks for the clarifications. +1 The "that would mean" kind of gives it away. I've been worried by this for some days now... Is Zeilinger endorsing superdeterminism??? I will get hold of this book and read the paragraphs in their natural logical flow, if you know what I mean. I did understand that the quasar experiment seems to rule out superdeterminism, though. But at that point it seemed to me that Zeilinger was considering superdeterminism as the only way out to save locality. That would be a big "oh, no!!" by me.

Sometimes you can look at the same fact from different perspectives... Example: In order to find its path from A, a particle follows the clue of velocity and force or, In order to go from A to B, a particle tries to minimise its action Both are mathematically equivalent.

Not all fields are scalar fields. You're implying scalar fields. Fields can be scalar, real, complex, tensor, spinor, vector... They can code fibres, curvature, torsion, topological numbers... Fields are abstractions, they don't have to be made of anything. They must comply with certain rules though.

Exactly. It's clarified in the next paragraphs. Zeilinger does not endorse "spooky action at a distance": (quoting Zeilinger.) The part highlighted in red seems to be implying superdeterminism. I would postpone that, because you have a dangerous tendency to mix up different topics. Suffice it to say that superdeterminism is just one loophole for someone who wants to save some kind of determinism at all costs. People who are familiar with mathematical proofs know very well that finding a counterexample does not necessarily imply the counterexample is unique. The part highlighted in boldface black is the most important one, which ratifies what @Eise is saying. Good. If you understand what you've said, you could be on the verge of understanding your own confusion. It's not a minor point. It's very important. It's the essence of the projection postulate, which is deeply non-local, but has no non-local consequences. Only problem: It's just a convention. It's not an evolution law for the state, and certainly not a law of physics. And most importantly, it has no experimental consequences. It was theoretically designed to do exactly that. Go back to my comment on FAPP's Bell's comment. Most physicists that contributed to the formulation of QM had no problem in seeing the state vector as just an epistemic book-keeping device, reflecting our knowledge. That's why they had no problem in introducing a non-local, non-unitary mathematical convention of which no non-local consequences could be derived. And last, but not least, as Eise has said above: No. Non-locality does not imply non-realism. They are very different assumptions. Example: Plane waves propagate in a totally local way. Yet, by virtue of selecting the momentum, the position is totally undetermined. That's local non-realism at its simplest, even before we start talking about entanglement. @bangstrom. You also said this in answer to @MigL: The quote is from Bohr, in answer to Einstein's famous "God does not play dice" --a colourful way of saying he didn't accept indeterminism at that point. But, really, is that "the explanation" of everything we're talking about here?

LOL. You've made a good point before, and something deep inside of me tells me you're about to understand an important part of this problem. Maybe tomorrow. Hint: You said "minor point." It's not minor at all. It's the key to all the confusion.

Here's a riddle for you: If there's no way to know which "action" came first --in a given frame of reference--, how do you know the time interval between the "actions" can be tagged as FTL?