joigus

(Quoting Hossenfelder.) Of course not: Quantum mechanics forces you to give up on determinism. Period. If you accepted quantum mechanical experimental success, but --in order to save determinism-- accepted some kind --any kind-- of internal determinism to account for it, you would have to give up on locality. Is that clear at long last? Let me guess: No. The problem with the starting sentence is that it opens the gates to a gross misunderstanding, if you remove the essential words "it seems." It's so common a misunderstanding that I don't care how much time I have to spend talking about it as long as the possibility exists that, finally, people who still think this to be the case, are gathered at the gates of quantum heaven at the end of days. This final day you will meet Feynman, Gell-Mann, Sidney Coleman, a repentant Einstein, Bohm, and a repentant Bell --"repentant" for having introduced confusing words in the first place, but redeemed both Einstein and Bell by their accurate and commonly misunderstood respective analyses--, and agree with all of them that quantum mechanics is local. Classical logic, if pressed to account for quantum correlations, would have to be implemented non-locally. But wait a minute, classical logic is not what quantum mechanics is about. End of story. Or is it? There would be a second loophole for the prophets of non-locality. What if the projection postulate is correct? The projection postulate is strongly non-local. It would be a kind of non-locality with zero consequences, by design, because the components of the quantum state that don't carry the actual output of an experiment, must be killed off by decree. Actually, if you think about it, it's no wonder that it entails a non-local prescription: It was designed to implement the fact that real electrons and photons hit the screen at some point. So you introduce definiteness at some point by design. If you remember Bell's theorem, and really understand it, there is no mystery. And that's all. If bangstrom finally has understood this point, we could perhaps proceed from there. The explanation of that monumental fiction: Why does the projection postulate introduce a non-local prescription that produces no non-local consequences? But something tells me we're not getting there any time soon. This would make for an interesting topic of debate on (bare evidence) + (bare assertions of a theory) vs (epistemological prejudices) of people: Illusion of design --evolution--, illusion of non-locality --QM--, and probably more. The theme is more general than it looks.

You are so confused. Let's take Sabine Hossenfelder's video and read carefully her statements. I'm reproducing here the most important ones with my emphasis: Is and is not local? Mmm. What could she mean? Appears to be? So what then? Is it, or is it not? More: In other words, some people choose to say it is non-local. It seems... mmm. Is that a strong statement to you? Here's the killer: If you quote authorities, the least you could do is listen carefully to what they're saying. I get it. Quantum mechanics seems to be non-local. But actually, it is and it is not. That's why some people choose to say it is non-local. Sweet. You could at least listen to the videos you post, @bangstrom

Exactly. Counting particles is beside the point. It's so easy to find examples of many particles in a maximally entangled state. Take any high-atomic number atom. Eg, californium's 4f energy level has 14 entangled electrons. The point is something else. Now, what is that something else? I'll be back. Running out of time now. See my point? Nature has done 4 better than scientists that prepared a 10-silicon-atoms entangled state.

Not surprised. I agreed to that one. Here's what I said: Water bear = tardigrade Essentially no different from experiment with a number of silicon atoms (the fullerene experiment.) There are other: https://phys.org/news/2017-11-physicists-qubit-entanglement.html You can take one qubit, coherently entangle it with another identical qubit, further entangle it with another qubit, and so on. It's an incremental process. I see no problem with that, except technical. Entangle a qubit with a whole bunch of atoms already involved in dissipative --irreversible-- interactions? Impossible. In fact, it doesn't even make sense: What does it even mean to entangle non-identical things? I understand I'm the party pooper here. Some people want to see extraordinary, magical things. Their will to do so takes them on a journey into foolishness and unsupported claims, as well as to drawing conclusions that are not there, and never were. It's all ordinary things. It's the world you see, none other. It's a cat looking at you and being there, alive through and through. Your life passes by before your eyes, and your cat is no longer there, keeping you company, as @MigL knows very well. What I would like some people to see is how magical, how extraordinary, ordinary things are. That's physics' "magic." It takes a while. It doesn't come easy.

Oh, an Iggy. LOL. Sure, as a joke it's really good. The claims of what it implies is what I find more "ignoble."

This is not peer-reviewed work. Cornell's repository is for preprints, not papers. I don't see the peer-reviewed paper anywhere. What I have found is a bunch of people saying this is nonsense: https://phys.org/news/2021-12-peers-dispute-tardigrades-entangled-qubits.html And I agree. I'll keep an eye on it just in case. Don't hold your breath. I see you have no idea how long it takes for a "groundbreaking" paper to get approved for publication, and once there, how long it takes for a Nobel prize to be awarded. You've watched too much Big Bang Theory. Give it a rest. And study some quantum mechanics in the meantime.

This is by far the most ridiculous thing you've said so far on this thread. You're being the mouthpiece of some fat-ass crackpottery, my friend. Through no fault of your own perhaps, just by constantly ignoring the physics involved. Really?, quantum coherent superpositions of order 1024 -plus individual electrons, protons, neutrons and photons making up a tardigrade, --I guess that's what you mean-- which is an animal that has dissipative processes constantly going on in its body? Now for buckyballs --I guess that's what you mean-- those are fullerene particles very common in interstellar soot, so I'm guessing it's possible in principle, like in the case of silicon atoms, although extremely difficult. I already gave you a reference to macroscopic superpositions of bunches of silicon atoms, but again you missed it. Give us the reference to your Schrödinger water bears, please. I wanna have a good laugh. Not only the square of the amplitude ψ∗ψ , but the probability current, which is conserved locally, as an exact theorem of quantum mechanics.

This is a very interesting point. People often change their views during their lifetime. Einstein is no exception. Even when the thinking of one particular person significantly contributed to change everyone else's interpretation, it's interesting to consider the challenges they had to face, the historical climate they stood up against, as well as their own thinking as an ongoing process, and get --be it ever-- the roughest feel for how their thinking must have evolved. I once read that it took Einstein one whole year to realise that Minkowski's 4-dimensional description of his own research was actually relevant. Even if that's an apocryphal story --which I don't think it is--, there's a potential lesson in it. We tend to think of scientific breakthroughs as kind of a static or frozen process, which they are surely not.

Just one: No classical object will serve as an analogue of a quantum system. (Anti-emphasis.) Don't tell anyone, apparently it's a secret, even if you repeat it 6 times. Here they are: Another one: Another one: Another one: Another one --with icecream; maybe it's the concept of coin that's standing in the way, who knows: Another one: It really looks like I've said something about that before. Maybe I didn't and this is all a non-local, superluminal dream. A coin (cat, gloves, icecream, etc.) has no states that are determined (elements of reality in Einstein's parlance) as to the Heads/Tails character, but a superposition of ·Euro/Dollar as to the "coinage" character, so it will never reproduce all quantum peculiarities. You couldn't, so it won't. When will a classical analogue spell out the properties of quantum systems?: No can do, very problemo, when Hell freezes over, never happens, when the cows get home and cook me dinner and sing me a lullaby... So I'm sorry, no classical analogy. You really must think quantum!!!!!!!! Please, tell me it is clear now. Yours truly, Sisyphus Edit: x-posted with @NTuft

I'm not looking for agreement. I'd rather you disagreed with me, or bangstrom, or any other, as long as you provided an argument for the particular point in QM where you see this possibility of superluminal communication, or instantaneous interaction, or what have you. On what grounds do you agree that "communication via entanglement is impossible now"? Are you saying that communication via entanglement will be possible without superseding QM with some other theory that is non-local? Notice, please, what I'm not saying: I'm not saying that communication via a quantum channel --whether it involves entanglement or otherwise-- is impossible. It's only that whatever communication channel will be subject to the strictures of local, sub-luminal propagation. Unless we come up with a theory that substantially changes quantum mechanics, and ushers in a new era with the possibility of superluminal propagation. Such a new theory would also have to explain why we've never observed it so far. Then, it would have to explain: How come relativistic causality is not violated?

If a person who doesn't really understand English very well overhears a conversation in English, and hears the words "red herring" he may be at risk of thinking these people are talking about a rare species of fish. That's similar to what's happening to you here. I'm sorry, you have proven to be a monumental loss of time to me. Many posts ago I introduced an example designed to illustrate that even classical physics can mislead you to the wrong conclusion if you hear an argument and, loosely, poorly, wrongly, interpret it in terms of just the words, drawing loose inferences from them. You (1st) missed the point, and (2nd) offered an analysis of the physical example --totally wrong, by the way. I'll finish with a clue for what may come next: Keep track of the phase changes in the components of the wave function, and the essential difference between closed quantum systems and open quantum systems, because I intuit that's what's confusing you, and many other people with you. @Eisewas totally right when he said that the illusion of superluminal signals only appears because one wants to understand what is happening from a classical viewpoint. I would add (repeat for the nth time really) that there's a second possible source of illusion of superluminal character that comes from the (valid for-all-practical-purposes --FAPP--, but fundamentally flawed, in Bell's words) projection postulate. I have two eyes. You have two eyes. The event that determined the astonishingly[?] precise correlation is far back in the past, somewhere in the pre-Cambrian seas, when the first animals developed eyes. You can measure the correlation between those facts with as much precision as you want here and in Andromeda. There is no limit to how "superluminal" this looks if you keep calling that a signal. Do you understand now? Is that clear now? Will we be talking about this totally trivial point forever?

Indeed. In order to capture all real-world degrees of freedom of gravity, you need at least a rank-2 tensor field. Scalar and vector fields aren’t enough. Indeed. You can build a workaround by using the formalism of differential forms and introducing the diff and the co-diff operators (the analogues of grad and rot.) The co-diff operator is a contraction of the epsilon tensor and metric coefficients with the diff operator. You're venturing into territory well-charted by others and without the proper tools. See: Differential Geometry, Gauge Theories, and Gravity By M. Göckeler, T. Schücker Cambridge University Press p. 40 https://books.google.es/books?id=Lr8zo2caBWYC&pg=PA40&#v=onepage&q&f=false

IMO, all hell broke loose when you said, (My emphasis.) You seem to insist on things like, Creating a communications pathway is precisely what is not possible. Also, all the degrees of freedom are present in normal matter and/or light. And then, you go on to say, If you use the channel so as to in any way break the coherence by interacting with it, the system is no longer entangled. In a manner of speaking, you have "selected" a subcomponent of the previous quantum state, thus destroying the richness of correlations it was packaging. You also say the topic "is not about standard quantum mechanics." What other kind of quantum mechanics is it about? When the system was prepared, it was correlated in any possible direction that you chose for the polarisers. If you set up a polariser, it is no longer entangled, but now you can predict something about the distant part. If you further deflect/filter any of the beams, it is no longer correlated at all, let alone entangled. What do you want to do with that? Most anything you do ends up destroying the peculiar quantum correlations, and you get closer and closer to the classical description. Not totally, because you still see a binary observable, which is not covered by classical mechanics for spinning object. But you no longer have the effects of entanglement. I hope that helps further clarify the discussion, but without us all getting muddled up into fantasy physics.

The metric itself is not a proper observable, really. What's a proper observable is the combination of derivatives of the metric and the metric coefficients themselves that makes up the components of the Einstein tensor. I still think this expansion would make sense in that it would reflect deviations from a model of universe with just matter density and spatial curvature. That, of course, provided the denizens of this universe had an individual --say Alf-- who was capable of deriving Alf's equations by just sitting and thinking about people falling in a gravitational field. That's what it took Einstein, if you think about it. Denizens of this universe, would be able to infer that Alf's equations allow for the addition of a term (constant)x(metric) that doesn't make any difference in the equations. So they would start thinking about this and at some point propose measuring this constant by measuring deviations from pure matter-density and spatial curvature solutions, perhaps by sending "people" far away and making measurements. The fact that something is very difficult to measure doesn't necessarily mean it cannot be measured, at least in principle. If you do have that other galaxy, perhaps you could devise high-precision methods to measure that deviation.

Correcting myself. You would obtain a state that's only 1/2 probability of being "Dollar" If you ask the question Euro?, you obtain a state that's only 1/2 probability of being "Euro" So, again, the conclusion is that when a state is "sharp" in one observable, it's "fuzzy" in non-compatible ones. Just in case someone's doing the calculations and fixing on what I said too literally. After all, projections are just an instrument to calculate probabilities, they don't tell you what happens to the quantum state after a measurement. This is very much in agreement with what seems to be the conclusion of the paper that @Eise posted: with detectors that are moving with respect to each other at constant velocity. As I already said:

Here's the problem with the coins if you want to understand quantum mechanics with them. There is an observable with two possible outcomes, and the corresponding eigenstates. States are 2x1 matrices: \[ \left|\textrm{heads}\right\rangle =\left(\begin{array}{c} 1\\ 0 \end{array}\right) \] \[ \left|\textrm{tails}\right\rangle =\left(\begin{array}{c} 0\\ 1 \end{array}\right) \] Yes-no questions are 2x2 matrices that satisfy that their square equals itself. In the case of heads/tails, \[ \left(\textrm{heads?}\right)=\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right) \] \[ \left(\textrm{tails?}\right)=\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \] Meaning of squaring the matrix (repeating the question): \[ \textrm{Is it still heads?}=\left(\textrm{heads?}\right)\left(\textrm{heads?}\right)=\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)=\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right) \] \[ \textrm{Is it heads when state is "heads"?}=\left(\textrm{heads?}\right)\left|\textrm{heads}\right\rangle =\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)\left(\begin{array}{c} 1\\ 0 \end{array}\right)=\left(\begin{array}{c} 1\\ 0 \end{array}\right)=\left(\textrm{yes}\right)\left|\textrm{heads}\right\rangle \] Etc. Incompatible questions. Suppose we introduce a question that's incompatible with the questions “is it heads/tails”? \[ \left(\textrm{Euro?}\right)=\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right) \] \[ \left(\textrm{Dollar?}\right)=\left(\begin{array}{cc} 0 & 0\\ 0 & 1 \end{array}\right) \] But hang on. This looks like the same questions. Indeed. The new question, in the so-called Dollar/Euro representation, looks like this, \[ \textrm{Is it Euro when state is "Dollar"?}=\left(\textrm{Euro?}\right)\left|\textrm{Dollar}\right\rangle =\left(\begin{array}{cc} 1 & 0\\ 0 & 0 \end{array}\right)\left(\begin{array}{c} 0\\ 1 \end{array}\right)=\left(\begin{array}{c} 0\\ 0 \end{array}\right)=0\left(\begin{array}{c} 0\\ 1 \end{array}\right)=\left(\textrm{no}\right)\left|\textrm{Dollar}\right\rangle \] What's hopefully illuminating is asking the (Dollar/Euro) question in the (Heads/Tails) representation. Here's how QM does it: \[ \left(\textrm{Euro?}\right)=\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right) \] \[ \left(\textrm{Euro?}\right)\left(\textrm{Euro?}\right)=\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right)\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right)=\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right) \] \[ \left(\textrm{Dollar?}\right)=\left(\begin{array}{cc} \frac{1}{2} & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{2} \end{array}\right) \] \[ \left(\textrm{Dollar?}\right)\left(\textrm{Dollar?}\right)=\left(\begin{array}{cc} \frac{1}{2} & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{2} \end{array}\right)\left(\begin{array}{cc} \frac{1}{2} & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{2} \end{array}\right)=\left(\begin{array}{cc} \frac{1}{2} & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{2} \end{array}\right) \] \[ \left(\textrm{Euro?}\right)\left(\textrm{Dollar?}\right)=\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right)\left(\begin{array}{cc} \frac{1}{2} & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{2} \end{array}\right)=\left(\begin{array}{cc} 0 & 0\\ 0 & 0 \end{array}\right) \] Wait a minute. What happens when the state is, eg, | heads 〉 , but we ask ( Euro? ) . Let's see, \[ \textrm{Is it Euro when state is "heads"?}=\left(\textrm{Euro?}\right)\left|\textrm{heads}\right\rangle =\left(\begin{array}{cc} \frac{1}{2} & \frac{1}{2}\\ \frac{1}{2} & \frac{1}{2} \end{array}\right)\left(\begin{array}{c} 1\\ 0 \end{array}\right)=\left(\begin{array}{c} \frac{1}{2}\\ \frac{1}{2} \end{array}\right)=\frac{1}{2}\left|\textrm{heads}\right\rangle +\frac{1}{2}\left|\textrm{tails}\right\rangle \] It mixes the answers in heads/tails. IOW, the coin is no longer heads. This all happens without me having even started talking about position. Space is even just one point for all I've claimed. What if you represent the outcome in the Dollar/Euro representation? You would obtain a state that's a linear superposition of \( \left|\textrm{Dollar}\right\rangle \) and \( \left|\textrm{Euro}\right\rangle \) –with a minus relative sign, if I remember correctly, but it would be a simple exercise to get the details. IOW: When the coin is “heads,” it's neither a Dollar, nor a Euro. You get me a coin that does that, and we would take the conversation from there with just coins.

'Quantum teleportation' is a very bad name for what it actually is: The possibility that QM affords you to select certain pairings of flavour (by drafting people with different sensibilities for different flavours) of a "magic icecream" that was prepared in Hamburg (so all its properties have been cooked up back there and then) in such a way that, if someone tastes it in Andromeda later, and other person tastes it in Australia, (and both have analogous taste receptors) and it tastes of vanilla, it will taste the opposite (whatever that means) to the person tasting it at Andromeda. But if you choose people with different sensory receptors, the flavours will be completely uncorrelated. Strange flavour properties for a classical icecream, right? Sure. The argument is a bit involved, granted. But if the whole setup was prepared in Hamburg, so that the strange flavour correlations were already present there, how is this mess --whatever it implies-- telling you anything at all about locality? If the x-position has been factored out of the problem, how can it be the case that it's telling you anything about the x position? If ever anyone were capable of making an icecream with non-commutative flavours, it would be obvious to us all where the real crux of the matter is. Because that's so far removed from our intuition, it will never happen. The problem with quantum mechanics, the real thing that's difficult to wrap your head around is that a perfectly defined vanilla-flavoured piece of icecream is made of equal parts of chocolate and anti-chocolate.

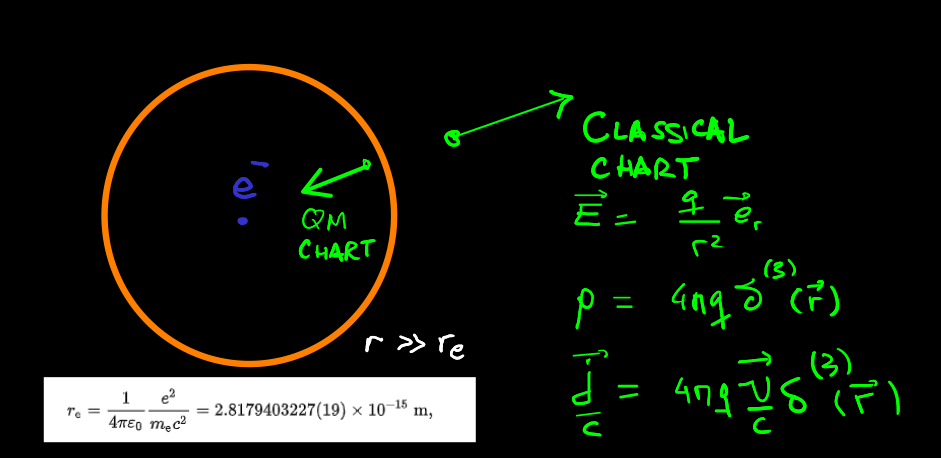
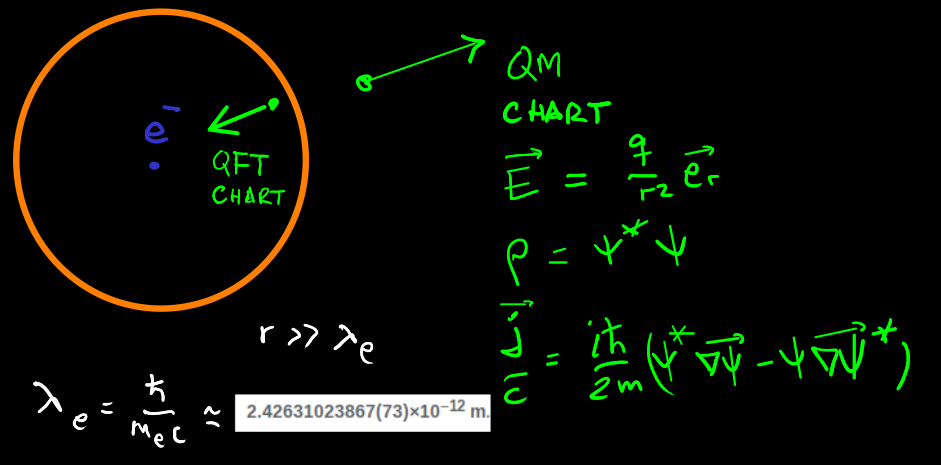
Sorry, I didn't mention that. I meant 2D surfaces. Once a time-like foliation is chosen, it would be a matter of choosing Sx[t1,t2] to consider the "objects" trapped inside the surface in terms of histories. The point is: Could it be that the different theories (classical field theory, quantum, and beyond) were related to the choice of local charts in the field variables? IOW, could it be that field variables are also inevitably affected by choice of charts in their field-variable phase space, each chart being a different domain, representing a different field-theory approximation? Something like what I'm trying to schematically represent in the following sequence of pictures: The orange circles represent the 2D-surfaces I'm talking about. OK. I'll keep re-cycling myself on these questions too, as I'm a bit hazy as well.

Right. You've convinced me. The EP is only valid locally, so I didn't apply it correctly. Now matter how you look at it --once you consider the galaxies are not constant-- the situation would be unstable for the two galaxies. If not for the loss of mass, the slightest anisotropy, or assymetry between both, would be enough to make the situation unstable for the galaxies, and they would be able to tell --eventually-- that spacetime is expanding. Ah, got it. That's what you mean by "step" right?

Absolutely. Good point. In the small scale, the solution would be unstable, and galactic observers would be able to tell there is expansion IMO. On second thought, you would need the minutest assymetry, and appealing to conservation of momentum. If it's just photons being lost in every direction, I think you could prove, based on the equivalence pple. that if either one of the galaxies is loosing them isotropically, as the CM of both would be placed exactly the same. Does that makes sense to you? I would have to go over the arguments more carefully. I'm using Newtonian approximation for the galaxies in my reasoning.

Of course I do. Give me some more time, please. Thanks for the reference. I'm aware of it. I didn't want to bring that up just yet. The peculiar epistemological position of quantum mechanics is that it postulates a different mechanics, but makes constant reference to a limiting regime that's not really in its formalism --it cannot be obtained as an assymptotic limit, but only through analogy--. But, in fact, you put it there from the very beginning as a hidden assumtion at some points. Classical mechanics appears in quantum mechanics only as a shadowy figure. Very much like melody in music. Perhaps we will be able to discuss it later. Or open a new thread about that specific question.

You cannot entangle two classical (macroscopic) objects. But there is no limit to how much entanglement you can get as long as you keep it microscopic and coherent --very delicate interactions. You can entangle a photon to another photon, to another photon, and so on. People have done that with silicon atoms, and they call it "Schrödinger cats." That's not the relevant situation with two holes drilled on a plank. You could correlate each hole with a spin-flip device that's behind at least one of them: If the particle were to go through that hole, the spin would flip. The interference pattern would be broken. Of course, at the end, you would have to have something amplify the signal. If you don't amplify the signal at any point (making millions and millions of atomic interactions get involved in the process), the interference pattern would still be there. That's my understanding. I haven't conducted the experiment at home.

The coin example is Swansont's. It is local. It reproduces one interesting aspect of quantum mechanics, which is superpositions: Until we measure, the coin is neither up nor down. What I've said is that no classical analogue can reproduce quantum mechanical correlations. So no coin, dice, gloves, cats, or whatever other classical mechanism can reproduce quantum correlations to their full extent. This is, in some sense, like a house of cards. If you remove one feature, the whole "quantum peculiarity" falls apart, and you get something in contradiction with actual physics. I gave an example before: If you removed randomness in a way that you could force a sequence of data --that would be an interaction; that would be writing a message--, while keeping the quantum correlations, and the validity of QM everywhere else, you would be able to exploit exact correlations for parallel polarisers to send superluminal signals, because the far-away observer would be reading the negative image of your message. Of course, that's impossible.

<Preliminary> I think one thing is how the motion of galaxies would be perceived by typical "galactic observers" (those people sharing the same galaxy and observing whatever other galaxies there are around), and another thing is how they would observe gravitation to work within their own galaxy. Yet another thing is what they would make of any other "components" of gravity (vacuum energy, spatial curvature) if there is nothing around as a reference. There's also the question whether that model of universe is consistent with Einstein's equations. It's an interesting question. </end Preliminary> My best guess is that your universe would be mathematically consistent, the galactic observers would notice nothing peculiar about gravitation in their own galaxy, but they would see a point in the sky that's always there, with no receding velocity of any kind, and changing in luminosity and features as it evolves, as both galaxies grow old, with the natural delay that we all know. But they would be clueless as to what keeps it there, assuming they would ever get to extrapolate that gravity was also valid for cosmic objects. The main problem I see is that this universe would be unstable, so the situation wouldn't last --in cosmological times. This is similar to Einstein's initial proposal of a static universe with a cosmological constant that's just so tuned to keep everything in place at large scales. I'm not sure if that's what @MigL means by "step" solution. There would certainly be a jump in the sign under even the slightest pertubation --let's say a bunch of more photons than average escape in the direction opposite to the "neighbouring" galaxy, and bam, the galaxies start separating forever. I've been playing with the model mathematically a little bit, and it seems to be consistent. I've taken as a basis the FRWL universe at large scales. Because the universe is mostly nothing (just two galaxies), assuming there's no radiation background, no DM, just k (spatial curvature) and vacuum energy. Don't forget that k, the spatial curvature, is an observational piece of input, as well as the vacuum energy and the density of different stuff. If you feed k=0 (which is what we observe in our universe), it certainly gives a static universe. Of course, you can't see the galaxies in the model, because the FRWL model is valid as an average for enormous scales of this mostly empty space-time that keeps expanding and expanding. So, as @zapatos says, who is to tell spacetime isn't expanding even when there's nothing in it? But I wouldn't worry too much, because one cannot measure empty space expanding with mostly nothing in it. All this, of course, is just my take, and presented as contingencies based on the models we know and how I understand them. On second thought, no --because of momentum conservation. I have to think more about this. LOL. Ok. A bunch of more photons than average escape in the direction towards the "neighbouring" galaxy, and bam, the galaxies start separating forever.