joigus

Not exactly. The combination of QM and GR seems to suggest a surface because of Maldacena's AdS-CFT correspondence principle, which I do not completely understand. It says that a pure-gravitation theory whithin a certain closed "bulk" of a space is equivalent to a corresponding gauge theory (a generalisation of electromagnetism) on the surface of that space (the boundary.) Why complex variables become necessary to describe micro-physics? I don't know. I'll give you my best guess: Maybe the whole thing is a problem with local charts for covering the field variables. Example: If you want to chart a sphere* with one global coordinate chart, it's impossible. You have to take at least a second local chart to map the pole that you've left out. Maybe what quantum mechanics is telling us [?] is something like: It's topologically impossible to map all of reality with one Cartesian/spherical-polar, etc., chart. If you insist on going "Cartesian cartographer" on something like an electron, you need to use a complex chart at some range, and then the problem of describing the "north pole" (where the electron is) becomes a probabilistic problem. Why does it become probabilistic? I don't know, and that does strike me as strange. * I really do believe that we should once and for all drop the dream of explaining everything with one parametrisation, and become humbler, like the cartographers of old did. We're nothing but cartographers, aren't we?

Planck's length and time are so incredibly small that I don't think we will ever be anywhere near what would be necessary to start seeing anything interesting coming from perturbative approaches, at least. Non-perturbative approaches are a different matter though. Non-perturbative approaches are non-incremental. So, who knows... I may be going wildly speculative here, but the fact that the mass Planck is neither here no there between elementary-particle scale and cosmic scale, seems to suggest something about information, levels of organization, etc. That kind of thing. But again, who knows. As @Markus Hanke has pointed out before --here or somewhere else, I don't remember now-- we probably need a quantum theory of gravity, the idea that bridges both, a metatheory of which both regimes are but an approximation. This again is, at least to me, a big "who knows."

Right. You got that, at least. The funny thing about all this is that neither you, nor any of these Neadau and Kafattose people, and other pop-scientists, book best-sellers, and vloggers you keep throwing at me --as opposed to all other no-nonsense actual scientists on these forums, and actually accomplished scientists who actually do understand-- actually understand what you got: The correlations are initial!!! So no non-locality. No superluminal signals. 1) The spin states are indeterminate 2) The correlations are initial Got it now? Gosh! Y'all pop-science people seem to be equally stubborn, if nothing else. And now I can absolutely tell that you guys got nothing else. Oh, by the way, I keep waiting fot that superluminal signal.

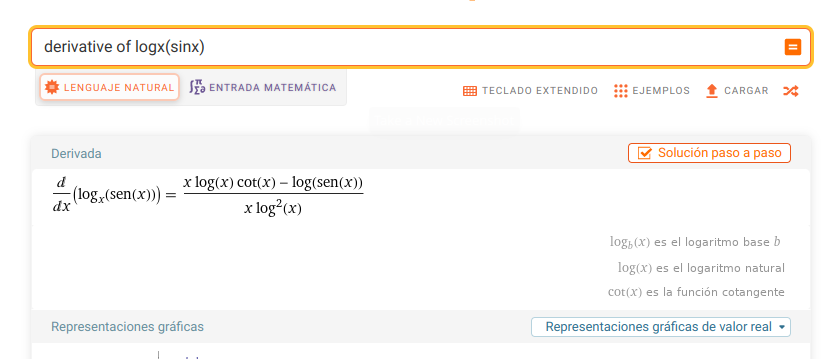
Here's the Wolfram Alpha output that --as I told you-- agrees with my calculation. But you will find no clue as to why it's correct. Cheers.

You couldn't tell locality from non-locality in a model if either one of them hit you in the face at 1000 miles a second. That much I have proven here. As to experiments, I'll give you ten years from now to point me to the experiment where any non-local effect of QM is proven. You can point me to anything from the past too, of course. There isn't. And my guess is that there never will be. If otherwise, QM would have to be fundamentally wrong. There's your experimental argument from silence, but a very solid one at that. I'll be waiting. This must be a joke. So where they able to send signals? No. They were able to check the correlations that I told you and proved to you based on QM, are there all along. (Sigh) Again, "spooky action at a distance" is just words, and very misleading by the way. There are no superluminal signals. If you and I think of the same thing at the same time (because we're thinking of something learnt by both before), and you decide to call it "action at a distance" just in order to sell more books or get more money for your experiments*, then that's your choice. Show me the signals, ie, anything that absolutely cannot be mistaken for initial correlations. Of course they measure "superluminal speeds." It's only because they're not the speed of anything. Let me make a prediction: Faster and faster "speeds" will be measured, with no limit. As fast the the time precision for the experiments is improved. And still nobody will be able to send a single blip of information. Wanna bet? * Or more clicks for your YouTube channel... Or...

The fact that a spin 1/2 cannot be expressed in terms of position and momenta has nothing to do with dimensions. Dimensional analysis is very useful sometimes, but doesn't give you all the answers by any means. It's to do with the general properties of the Hilbert space of position-momentum. First time people realised you need a quantum mechanical operator of angular momentum that generalises orbital angular momentum was because of splitting of spectral lines in hydrogen (anomalous Zeeman effect) that had nothing to do with the orbits, but must be something "rotational" because it was a coupling to a magnetic field. Then they went back to the QM's drawing board and formulated the general properties of an angular momentum, and discovered that there was room for this subspectrum that jumps in half-units of \( \hbar \).

You're very welcome!

Do not totally despair. You at least mentioned the magic words "CSCO," which are absolutely key to understanding why there is no non-locality here. CSCO = complete set of commuting observables The state, written as, \[ \left|\psi\right\rangle =\frac{1}{\sqrt{2}}\left(\left|\uparrow\downarrow\right\rangle -\left|\downarrow\uparrow\right\rangle \right) \] as commonly used in the literature, does not tell you anything about the position representation --the part of the state that tells you where the probability amplitudes in position are centred around, how spatially-spread they are, etc. Expert physicists, who write about this for the benefit of laypeople, do not tell you about this, only because the discussion would become too involved technically, and because nothing essential to be discussed depends on it. Why not? Because the Hamiltonian after the decay commutes with the position spin variables, so the evolution operator, which is an exponential of the Hamiltonian, does too. So no spin-odds depend on that. That's why the correlations, bizarre thought they may be, carry no information about locality --or lack thereof-- of the quantum state. Is that clear, @bangstrom? If it's not, I can't help you any further. I'm sorry. https://inst.eecs.berkeley.edu/~cs191/fa07/lectures/lecture13_fa07.pdf

I just asked WA, and totally agrees with my calculation. I can PM you solution from "Fram" if you want. Cheers

Analogically, with electric fields? Like a 2-D model of a womhole? I'm intrigued. The thing that's more "analogically" similar to gravitation is electrostatics...

Agreed. Very nice analysis, by the way. What surprises me is not that the entropy is finite, --something Bekenstein and Hawking taught us to think about in terms of QM--, as much as the fact that a classical BH would have an entropy at all, never mind --for the time being-- it being infinite. This is the key to my twice-emphasised: Suppose a civilisation more familiar with both BH's and entropy than our scientist ancestors have been for centuries, and didn't know QM, came to study BH's very much like physicists of the 19th century came to study the black-body radiation. The Planck of this civilisation solves a puzzle for a generation of these physicists. What is their puzzle?: all calculations of a BH's entropy give infinity! Let's call it the ultra-entropic catastrophe, in close analogy to the ultraviolet catastrophe that gave rise to QM. The solution to the puzzle comes in the form of regularising the entropy by means of quantising the action variables on the denominator so that the entropy doesn't come out infinite. That's what the HB formula for the BH seems to be suggesting. Now that's what I find very surprising. What is that infinite entropy that the quantum equation is suggesting if we "classicalise" the BH by doing h-> 0? What are these classical variables, all scrambled up, that QM needs to regularise?

I think you missed the most important part of MigL's post:

This is the point that I've been trying to get across for quite a while. Thank you!!!

OK. This kind of says it all. The same maths work both for locality or non-locality depending on what words you use to describe what you see in those maths. That is what you're saying. So it's just a word that you put on top of the maths that says whether some pattern of evolution is local or non-local. (!!!) Later, as it was just meant to illustrate 1) how words mislead you easily in physics, and 2) your misunderstanding of basic physical concepts. For better or worse, sanity checks take a lot less out of one than insanity checks. And I'm afraid your "current authorities" have a lot much of the first attribute than of the second one. Funny. You said the EPR was "discredited." Now Einstein is summoned here to save the day for the believers of spooky action at a distance. Quite honestly, I don't know what to do with that. Non-locality is a time? Rather, non-locality (or its negation) is an attribute of the evolution law, the law that tells you how the state of a system is updated with time. Before I spend --presumably waste-- more time talking about the meaning of words, let's go for my sanity check: If \( \varphi\left(x,t\right) \) is a scalar (number-valued) field on the real line, \( \dot{\varphi} \) is its time derivative, \( \frac{d\varphi}{dx} \) its spatial derivative, and \( f \) is an arbitrary numeric function, which one of these models is non-local, which one has propagation at finite speed, which one has no propagation at all, and for which one it depends on some non-specified conditions? \[ \dot{\varphi}=f\left(\frac{d}{dx}\right)\varphi \] \[ \dot{\varphi}=f\left(x,t\right) \] \[ \dot{\varphi}=f\left(\varphi\right) \] \[ \dot{\varphi}=\frac{d\varphi}{dx}+f\left(x,t\right) \] You can give that to your authorities if you want.

Mmm. Part of what you say makes sense, and is correct AFAIK. The Schwarzschild radius of an object is essentially its mass. The Compton wavelength of an object is essentially its inverse mass. That's right. Both lengths meet at a particular scale we call Planck's scale. So you could define Planck's mass, eg, as the mass of an object of which its Compton length is the same as its Schwarzschild radius. Those are not ordinary objects, as you can imagine. Something that, in my mind, is extremely peculiar is that Planck's length and time are unfathomably small, while Planck's mass is roughly the size of an amoeba. Another very peculiar thing is that ℏ appears in the denominator of the entropy of a BH. IOW, it acts as a regularising factor for the entropy of a BH. If you make it go to zero, the entropy of the BH becomes infinite... Classically!! Now, there's a clue for you. Another part of what you say, I find more difficult to grasp, let's say. The Compton wavelenght of the universe doesn't make a lot of sense to me. The Compton wavelength is relevant in a context of quantum fields. When you try to probe a massive quantum field at scales of order its Compton wavelength, what happens is that, instead of getting a more detailed picture of it, you produce more quanta of the field and its associated anti-particle (2mc2 and beyond). IOW, you enter the regime of pair production. This is known as Klein's paradox --well, the solution to it, to speak more properly. I can't wrap my head around that for the universe!! Creation of universe-antiuniverse pairs? I don't agree with "everything is nothing but velocities and momenta." Spin is a good example. In quantum mechanics you have orbital angular momenta --things like xpy-ypx--, and rotation variables that cannot be expressed in terms of position and momenta (spin, more in particular spin 1/2.) We're talking generalities here, of course, but I think QM is probably the reason why very small BH's and very small regions of BH's cannot be understood in terms of classical GR. And very likely the solution to the problem of singularities is past that frontier.

Let me guess... It's either time for lunch or time to go to sleep. The second one is my present position.

I'm always wary of these terms politicians use to define themselves: Democrats, liberals, neoliberals, progressives... Democracy, liberty, progress. Yeah, sure. Gimme some of that, please. No political party will define themselves as "deceptionists" or "prejudicialists", or "spin-doctoralists." The ad will tell you nothing about what the product is. I suppose the Swedish must eat their pudding before they know what it's really made of.

Thanks both for your thoughts. I prefer to be optimistic, and look at it as the opening of just another niche. The rules and criteria must evolve, in keeping with the new conditions. I would like to set my hopes on this kind of thought: The audience of the talk that I posted, with their questions and observations, --they were all very young-- gave me a glimmer of that hope.

Internet algorithms --probably-- have lead me to an interesting talk. I'm trimming it up to the point where the concept appears: The term appears to be standard enough that there's an article on it on Wikipedia: https://en.wikipedia.org/wiki/Splinternet Several developments on these forums have led me to think there must be a nugget of truth at least about these things. It feels like strong "reservoirs" of opinion, no matter how weakly unsustained by facts or logical consistency, seem to thrive much better than ever before on the Internet. Are these phenomena real? Were you familiar with them?

Sorry, mistake there. They're not pedalling downhill either. But anyway. Feel free to ignore the cyclist's story from here on out. To the point. What exactly is non-locality? Get ready, for my next question is going to be: Which one of these (2-3) mathematical models of evolution is non-local, and why?

No, no. You go. What is non-locality to you? So far, I'm the only one of us that's shown you the calculations and basic principles (conservation laws, observables, quantum evolution, maximally entangled systems) at play, in a way that seems to be to, at least to a certain extent, to the satisfaction/agreement of everybody else but you. You've shown nothing but your unconditional adhesion to a well-known silly and incorrect interpretation that's been running around for decades to the desperation of many renowned physicists. Then I give you a simple problem in classical physics to illustrate how if you try to solve a "paradox" by using words instead of writing down the maths, you can be easily mislead. You don't even understand that simple problem (the cyclists are not pedalling downhill; rather, they're falling downhill, etc.) You misinterpret every single thing I say. That was designed as a test for your attention span. And the key to why you misinterpret the physics is in your own words: (My emphasis.) It takes a lot more than a quick view of the literature to understand physics. So now I think it's your turn. What is non-locality? Be careful, because physicists use this term in loosely overlapping senses sometimes, and it's necessary to tread carefully. This is not something that you will be able to sort out by googling it up in a couple of minutes.

OK. No problem. Trying to be cautious here, I wouldn't say it's necessarily just an artifac. But it's not telling you anything that's not already implied by the theory you're working with. Could it be giving you a clue about something? Perhaps. I don't think that's the case, and the reason is quantum mechanics. And quantum mechanics tells us it's rather an area that's important. In its most elaborate version this has come to be known as the holographic principle. The two fundamental universal constants in GR are G and c. You solve the equations for a particularly simple case, and it tells you that at r=2GM/c2 something peculiar happens. You call this radius associated with a BH of mass M its Schwarzschild radius. Now you consider different M's and divide them by their corresponding RSchwarzschild. It gives you always the same ratio, which is a universal constant. What else could it give you? The Schwarschild radius of any M is proportional to that M, and the constant of proportionality is a universal constant. There's a similar situation with quantum field theory. There, what you have is \( \hbar \) and c. For any object of mass m it gives you a characteristic length, called the Compton wavelength, which is, \[ \frac{\hbar}{mc} \] It does play a special role in the theory. But the fact that the product of an object's mass times its Compton length gives you always the same value, does not necessarily tell you anything that's not already implied by the theory. When you try to put together quantum field theory and GR, at least on dimensional grounds, you do obtain a clue that the really deep quantity is not a length, but an area. I suppose what I'm trying to say is: The problem with dimensional analysis is that there is no unique way to interpret one of these "coincidences." I'm a bit tired now. I need some sleep.

This reminds me of an old debate I had with someone who asked me if/why a cyclist who is more massive than another has an advantage when going downhill. I said he does. "Is it not true that the acceleration of the cyclist does not depend on how massive he is? So both the massive, and the less massive cyclists would experience the same acceleration." "Yes", I said. "For cyclists falling downhill on a frictionless slope, that's true. But you're forgetting friction." "But is it not true that the friction coefficient does not depend on the cyclist's mass either? "Errr... sure." I said. If you listen to the argument like that, in words, it sounds like he was right. But, Because he couln't be bothered with writing a simple equation, he was incapable of understanding why I was right. In the first case, the acceleration is the same because the force is proportional to the mass. In the second case --with friction-- the force of gravity is still proportional to the mass --necessary for acceleration to be the same in the 1st case--, while the force of friction is not. That's why the acceleration is different. The things that are independent of mass are different things. The problem is, if you just follow the words, you're incapable of understanding the reasoning. Words in physics, by themselves, are very deceptive. If the probability amplitude, with its correlations born in it, can be written with the spatial terms factored out, it's precisely because it doesn't matter where they are as long as we don't measure spin. The spin structure of the state was the same when the particles were together. It's like the person in my story. He was puzzled. We're saying the same thing! Yes, but you're interpreting incorrectly, and drawing wrong conclusions! Is that any better?

I don't have glitter, but I'll try my best: Now that I've learned the magic words?: I'm out.

I was. I said "probably," plus I didn't say Einstein was misquoted this time. I just said he's often misquoted. Probably more than anybody else. I'm making room for the possibility that Solomon communicated telepathically with Einstein, or knew him personally.