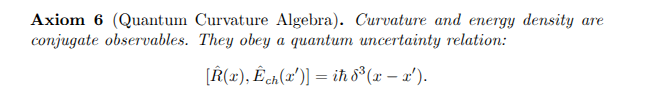joigus

Your ignorance of physics is Mariana-Trench deep. Perhaps only comparable to your hubris. "Virtual particles" is just a fancy name for fluctuations of quantum relativistic fields that can go off-shell for fleeting times. The number operator in QFT for virtual particles gives zero for the expectation value, as it should. Suggesting there are something in the ballpark of 1034 virtual particles (per what?, per unit volume?, in the whole universe?) just because the value of Planck's constant suggests you so strikes me as a feverish hallucination. Oh, and Planck's constant can be said to to go to 0 in a certain sense (although that's not exactly what we mean when we say that)*. But it makes absolutely no sense to say that it tends to 1. You see, it's not a variable: IT'S A CONSTANT!!! Never mind. You might not read a lot from me on any of your threads from now on. And please do correct your syntax and spelling, it seriously interferes with your clarity. Good luck. *What we mean when we say that is that every characteristic quantity with the dimensions of action in the problem under consideration is huge in comparison to \( \hbar \).

I meant thermal DOF, not geometric DOF. IOW, what are the microstates? To this day, nobody knows for sure what the microstates of a BH are. There are proposals, but not a mainstream explanation, AFAIK.

Then edit your post and correct it, as I do. Members shouldn't be striving to understand what you're trying to say. Also, don't put my words in your mouth, and use the quote function correctly. It wasn't you who made that comment about similar quantities at infinitesimally close point and different quantities at the same point. I was. Your physics doesn't make sense either. You don't understand the difference between the configuration space and the phase space. It's obvious you don't even understand the meaning of Planck's constant. Besides, it's not 1.054571817...×1034, but 1.054571817...×10-34. And it has dimensions of (energy)x(time), or equivalently, (momentum)x(distance), or equivalently, (angular momentum). Therefore, it wouldn't, shouldn't, and can't represent a cardinal (number of objects). I'll say it again: Jeez!

You start with a coarse-grained version of space, and explicitly introduce a preferred time, but you deny there is space-time in your model, although we can all see there is. You implicitly introduce gravity fields, because you illegitimately use G, thereby making room for fields with the dimensions required by gravity, but you call them "photons". The LLM you're using, instead of correcting your mistakes, helps perpetuate in your mind the false impression that you've come up with a novel idea. The lack of testable predictions should be a powerful clue that there's nothing there. When I say "testable predictions" I mean real ones, not things like, Didn't we agree this "photon collapse" was not gravitational? By the way, there is no reason in GR not to consider BH formation from just photons. Some models actually do that for the sake of simplicity, although that's not the way it happens in actual collapsing stars. Or, Redefining something with nice-sounding words is not a prediction. What are the degrees of freedom of the curvature field? A smooth curvature field does not have anything in the way of thermality. It doesn't look like you've explained that. This is getting almost painful to watch. I couldn't agree more with @Ghideon that you're engaging in ontological (or at least conceptual) bootstrapping.

I should have said "On the left hand side, we have the average perpendicular component of the electric field per unit volume with respect to..." You see, it's not easy to condense the meaning of Gauss' law into a handful of words.

I will say it again (apparently I need to say things three or four times before they get through): You have a fundamental confusion between non-commutativity in (pseudo)Riemannian geometry (non-commutativity of similar quantities at different but infinitesimally close points) and non-commutativity in QM (non-commutativity of essentially different quantities at the same point). Geometric quantisation is about commutation of dynamical functions (= phase-space functions = functions of x and p) evaluated at the same point (x,p) of phase space. Lie brackets, connections, curvature, etc, are about commutation of local functions in infinitesimally close points of space. I'm not saying there couldn't be a bridge between both notions. I'm saying both things are different and you haven't built that bridge AFAICS. Then there's the small business of connecting all that to the free parameters of the standard model.

Ah, but it's secretly the speed of light what's at play. If, mysteriously, the speed of light changed overnight. The day after that, antenna designers everywhere would say, "holy Molly, the impedance of the vacuum must have changed!".

I should have said "per unit volume" throughout that sentence. Never mind.

I'll try to save you some trouble. I can only hope... \( \pi \) is there just due to a convention in the units of charge. Coulomb, I'm afraid, got us all into a mess when he chose the units of charge to be what they are today. He chose the electrostatic force between two charges \( q \) and \( q' \) at a distance \( r \) to be, \[ \left|\boldsymbol{F}\right|=\frac{qq’}{4\pi\varepsilon_{0}}\frac{1}{r²} \] For Gauss, it would have been rather, \[ \left|\boldsymbol{F}\right|=qq’\frac{1}{r²} \] Where did the \( \pi \) go? It was absorbed into the units of charge. It needn't be there in the first place. So there's nothing like "pi in the impedance of the vacuum". In fact, "impedance of the vacuum" doesn't really mean anything. It's just the product \( \varepsilon_{0}\mu_{0} \) that means something, being the inverse square of the speed of light in a vacuum. For decades, Russian books of physics by MIR publishers were based on this system of units, as well as centimetres, grams, seconds. If you do that, units of charge have the funny dimensions of (mass)1/2(length)3/2(time)-1. I once won a bet based on this fact. Of course the \( \pi \) must appear somewhere else. And when you do that it happens to appear in Gauss' law, \[ \boldsymbol{\nabla}\cdot\boldsymbol{E}=4\pi\rho \] The meaning of this is: On the right hand side, we have the average perpendicular component with respect to the total closed surface containing a charge distribution multiplied by the total surface. And on the left hand side we have four times pi times the charge density inside that closed surface. This equation has the property that it doesn't change when you apply an arbitrary rotation to it. It's so-called spherically symmetric. Thereby the \( \pi \). Forget about "impedance of the vacuum", "electric permitivity of the vacuum", and "magnetic permeability of the vacuum" or whatever. This is long-ago-superseded Nineteenth-Century legacy lingo from people who didn't understand relativity. It is a sorry mess and has led generations of thinkers into a whirlpool of nonsense. And it still does. \( \pi \) in theoretical physics always has to do with rotation invariance. Full stop.

Agreed. There's perhaps no simple definition of a "degree of irrationality". For lack of a better term, I would call the one based on continued fractions a criterion based on how non-algorithmic the approximation is, the one based on Liouville's numbers a metric definition, and the one based on polynomial equations an analytic one. Which one is more relevant as concerns natural laws? One can only wonder at this point.

This kind of says it all, doesn't it. I'm too tired now. Maybe tomorrow.

You're right. It's not. It's the most irrational number according to iterated fraction decomposition (or whatever it's called). That's what threw me off and I (incorrectly) included it in the list. Thank you. Continued fractions. That's the name. It's more irrational than any other irrational number, but not transcendental. "More irrational" meaning the next continued fraction approximation is about as bad as the previous one. Meaning, \[ \varphi=\frac{1}{1+\frac{1}{1+\frac{1}{\cdots}}} \] because there's always a 1 coefficient in the next iterative step. Really appreciated +1.

I apologise for being a tad sarcastic about Plank and Planck, impute and input, etc. I should know better. It's perhaps worth mentioning that this π has nothing necessarily to do with the other π.

There are so many things wrong here. Where to start? First, even though nothing you say here makes much sense, I gather that you have a fundamental confusion between non-commutativity in (pseudo)Riemannian geometry (non-commutativity of similar quantities at different but infinitesimally close points) and non-commutativity in QM (non-commutativity of essentially different quantities at the same point). Also, how in the name of blazing hell is a collection of ones and zeroes a good representation for gravitons? Plus you cannot define a sensible position operator for photons. Let alone gravitons. In a relativistic gauge theory x and p must be replaced for something else, more akin to E and B (electric and magnetic field). Jeez!

They are created after spacetime? Mmm... So something happens after time... Your theory is a contradiction fest. Time after time.

Pi is not only an irrational number (one that cannot be expressed as a ratio of two integers). It is also a transcendental number. That means pi cannot be the root to any rational-coefficient, finite-order polynomic equation. Irrational numbers are kind of like "the beyond" of the realm of numbers (and ironically most of the numbers that exist). Transcendent numbers would be something like the beyond of the beyond. That's the realm of pi, e, and phi (the golden ratio). It would be highly suspicious that any simple argument gave as a result that pi has dimensions. Dimensional quantities are by their sheer nature ruler-generated multiples of a unit (a number that represents 1 in our scale). Any argument purporting to prove that pi is dimensionful would have to be labyrinthine, transcendental itself, based on infinite series at the very least. So I don't think so.

Good one! I would call this a "virtual split".

Oh. That one is even more spectacular! Only pi, e, and -1 involved. But then our friend would tell us e must come from some physical law. Yes! The topic is unending. I would conclude following in The-Princess-Bride style: You keep using this number... I do not think it means what you think it means.

Pi can be shown to be relevant in mathematics from many angles --pun intended. One of them not having to do with circles at all is the Basel problem: The sum of the reciprocals of all integers squared equals pi2/6. It's, of course, obviously dimensionless from here too. This had mathematicians scratching their heads for quite a while.

Oh, there must be a reason for number 2 as well then. Otherwise we would live in a matrix. Also, Planck scale is a physics problem, while Plank scales are presumably an engineering one. And nobody would impute anything to a number, although people input numbers every day. And lastly, but not leastly. Yes, we know there are bound to be facts without explanation in this post-Gödel, post-Turing era. A likely example is the Riemann hypothesis.

Ok, I'm talking off the top of my head, but I don't think matter shrinking everywhere would have equivalent effects to an overall acceleration. It would affect the energy-momentum tensor* on the RHS of Einstein's equations that would be impossible to factor into a scale parameter in the way of a Hubble factor. I think, without realising, you're thinking about a trivial rescaling that's nothing to do with an actual (active) transformation. Plus I still don't see anything "fractal" going on here... * Here, I've found one of Markus' objections that I think pretty much expresses the problem with the shrinkage, only perhaps much better than what I said:

That's not the point. Conjugate pairs of the field variables must comply with the principle of microcausality. Field values at space-like separated points must commute (or anti-commute if they are fermionic) and be canonically conjugate only at points time-like separated or null. No, you're not describing spacetime as emergent; you're saying you're describing it. Saying you're doing something is not the same as doing something. You wouldn't even have photons, very much in the spirit of what @Markus Hanke told you. In order to have quanta of a field the way we understand them, you need to establish commutation rules according to local values. Otherwise you don't even have quanta (and therefore photons). You wouldn't have spin, you wouldn't have on-shell/off-shell separation, or mass, or energy, momentum, Fourier transform of the fields. Nothing makes sense in your theory as far as I can tell. You haven't bothered to define such concepts as pre-geometric substrate. Using new words as shields against legitimate criticism doesn't do the trick. I'm sorry.

I also have a problem with your "stationary" chortons. Re-phrasing what @swansont said: How does gravity propagate then? Gravity is known to propagate. You say, You keep saying this. What region do the photons concentrate into? You say yourself there is no space, or time, or way to measure or define distance. You also say, That's not what conjugate field observables do in QFT. You're missing a very important consistency part. But I'm not gonna tell you what it is, because if I do, you will feed my objection into your garbage-generating LLM, and it will make it look like you're making sense. So I'm not giving you any clues. Let's see if you can figure it out by yourself. Thus far, your commutation rule does not make much sense according to relativity. It's too "crude". There are many more objections, but it's impossible to be complete. Let's start with those two.

Yeah, ambiguous question: The age of quantum computing? It hasn't happened yet. The age of quantum mechanics? It's been going on since the 1920s Some age or other in Planck units? I don't think that's what you're asking.

AHA! She's quite fond of TIT for TAT, plus MUM's her word, obviously.