joigus

Sorry, I meant: because all the other alternatives that were coded in the quantum superposition in some sense disappear. I'm sure most people understood that. Funny summary. Funny too, but in the other sense. It is my impression that if you sit long enough and think about Bell's analysis, you're bound to eventually find yet another possible loophole for some kind of "weak realism", or another. Maybe some kind of "emergent realism," or "fiduciary realism," as I tend to see Bell's beables, "superdeterminism," "hypercontextuality." I'm expecting new fancy concepts, most of them probably not very compelling, and having to face the inevitable sharp edge of Ockam's razor. The inspiring mood being: Try to find a way in which you can weaken the reality hypothesis, and you can find a way out. I was in the middle of writing this when @MigL's comment popped up, very much in that direction:

Sorry. Omission: the later one is in the future light cone of the previous one. And that is agreed upon by all observers, according to SR.

Crudely speaking, a theory is local when you can define quantities point-by-point as densities of something (energy, probability, angular momentum, charge, etc., per unit volume), then define current densities from them: the corresponding quantity (energy, probability, angular momentum, charge, etc., per unit surface, and per unit time) that escapes out of that volume through the boundary. For local theories, every quantity that is conserved, in order to leave the volume, must do so going through the surface. In other words, all these conserved quantities satisfy a local conservation law, which reads, rate of change of quantity Q within the volume V = -(flux of current density of Q through surface S) where S is the boundary of V, but otherwise S and V are arbitrary, and Q is any of these conserved quantities. All quantum theories are local in this sense. But the tricky thing is that all these densities become probability densities when quantum mechanics operates at the bottom of it. What people (sometimes, quite loosely, quite sloppily) call "quantum non-locality) is not that. Quantum theories allow you to prepare states that have no definite value of these locally-conserved quantum numbers Q, and then measure their value at the boundary. So you force the quantum state to "decide" (select, einselect) what particular value of the quantity Q it --for lack of a better word-- "encapsulates." You can do pairs of measurements for space-like separated events (so no light ray can join them) or for time-like separated events (so the time ordering between the events is observer-independent: the later one is in the light cone of the previous one). That really doesn't make that much of a difference. And it doesn't because all the alternatives that were coded in the quantum superposition in some sense disappear. Do they go to different branches of existence, no longer connected to the branch we see? Gell-Mann/Hartle style Do they escape away in the form of empty waves, never to be found again? á la Bohm Do they immediately disappear from existence, as the Copenhagen interpretation tells us? Nobody knows. Only theorists really worry about this. And cosmologists, both experimentalists and theorists. None of these possibilities affords any way of exploiting non-local effects because they have no non-local consequences. I could go into more detail about why that is, but suffice it to say that the same flow of probability density for V volumes and their S boundaries is satisfied. Only with a sharply defined value for Q now. And the state, as you already know, is always random in other quantities (those incompatible with Q.) There is logic in there of the type you use and I think you could critique it. I noticed studiot so maybe he can tell if this is worth a damn, too. Thank you. I'll take a look ASAP. Thanks!

Aha!!! +1. Good. You really want to understand this. I've found what's confusing you. The reason is this: This doesn't happen if you don't re-entangle the boxes. If you open the box a second time, or a third time (without bringing the sub-systems together again!) it will give again, and again LH. And again, and again... Unless some further interaction flips the spin or makes it precess, etc. But then, the spins never become correlated again. Or... If, on the other hand, as you say, you make them "somehow" entangled again, you get them back down to a singlet, and re-start the process, you do need to bring the particles together again. This "make them interact again" is what you say yourself (I repeat): Don't dwell on the confusion: They are always random, always! What's unmistakably quantum is not the fact the they are anticorrelated (we can reproduce that classically: boots, gloves, coins...), not even that they are random (we can reproduce that classically too, by introducing stochastic terms in the evolution equations), but the nature of the correlations that comes from non-commutativity. That, and only that, you cannot reproduce any other classical way. I repeat: If you want to re-entangle them again, you must bring them together again. See how (obviously, I would say!) it is totally local? The postulate of projection is what introduces irreversibility in the world by hand, by an ad hoc assumption. What I've just told you is completely contemplated by the projection postulate: https://en.wikipedia.org/wiki/Mathematical_formulation_of_quantum_mechanics#Effect_of_measurement_on_the_state IOW, immediately after a measurement, the state is an eigenstate of the observable you've just measured, so it gives you the same value with a 100% probability. When you project a projection, it gives you the same projection. That's the definition of a projection. The problem is, of course, that we cannot make this rule (that works perfectly in every other sense) comply with the Schrödinger equation. That's the ultimate reason why Zeilinger is inevitably led to say --in the reference you provided, And that's because there's no agreement, really, as to what happens after the measurement. Particles that become entangled need to do so by means of local interactions. If you study field theory, this becomes obvious. That's why all field theorists, Weinberg, Salam, Gell-Mann, 't Hooft, etc., have always been so little impressed by these claims of non-locality.

More comments on Dance of the Photons (my emphasis in boldface throughout): Zeilinger on how Bell's theorem is not the weirdest theorem in the world: I said: Zeilinger on standalone realism itself being at stake in the whole question: But QM already takes care of that => No-hidden-variables for spin, according to the theorems. In this particular connection, I said, Therefore, QM violates classical logic. Period. Zeilinger about how the argument of locality does not play a role in the Kochen-Specker theorem: and I also said, There are more points coming, but for the time being, suffice this to prove that Zeilinger's view is pretty much overlapping, at the very least, with what I've been saying here, and that you haven't the faintest idea of what you're talking about. Now, I hadn't read Zeilinger's book, and I'm very grateful to @Eise for facilitating me the reading of the most significant passages of the book. It's not very difficult for me to "read his mind," as it were, because I've been thinking, reading, and calculating about these topics very seriously for 40 years. I'm not reading anything I didn't know. I hadn't read about superdeterminism or thought about it in any length, because I've never thought it was a serious alternative. Now I'm sure Anton Zeilinger doesn't support it either --thank you, Eise. Now you tell me where I --and most other knowledgeable members-- have misunderstood quantum mechanics, @bangstrom. And please answer Swansont's question once and for all or, with all due respect, "collapse" into the mute state for all that concerns this thread, unless it is for the purpose of stating your thoughtful disclaimers, which I'm sure everyone would accept immediately.

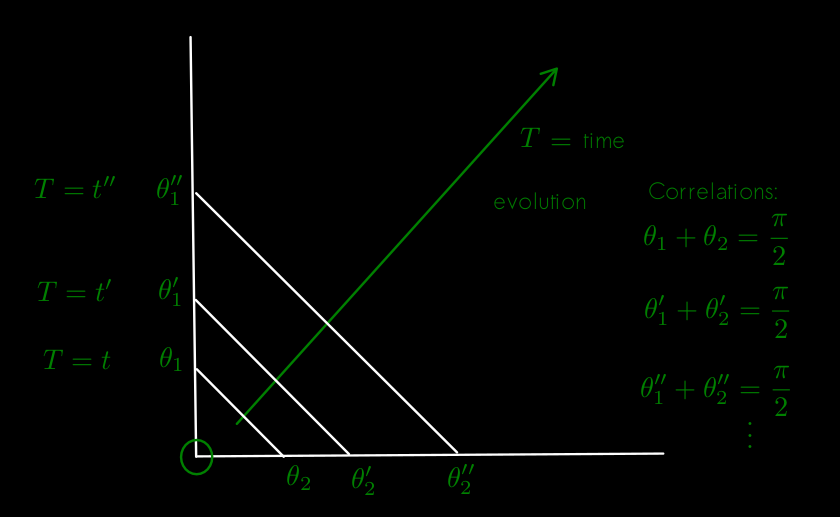
@studiot is not talking about the book he referred to before. He is now making a new argument, designed to help you understand a point very similar to one I presented before: The anticorrelations are built into the state, very much like the Pythagorean theorem is built into the relations of a right triangle, for example --a similar example to the one he is proposing. He is proposing that infinitely many possible values of an angle can be associated to a given value of a trigonometric function. And that should be no surprise, nor it implies a "spooky action between angles." Nor should it be any surprise that the two non-right angles of a right triangle correlate to \( \vartheta_1 + \vartheta_2 = \pi / 2 \). Continuing on my example of the right triangle ("the speed at which the Pythagorean theorem is true is infinity"), but inspired by Studiot's example of the angles: You can take as analogues of quantum evolution the right triangles getting bigger and bigger; the analogue of the correlation, the fact that they add up to \( \pi/2 \), and the analogue of being a singlet state (scalar representation of the rotation group), the fact that the triangles evolve while keeping the geometric ratios (analogue of unitary quantum evolution as well.)

Good point. +1 I've come to a point that I even accept the possibility that not only aspects of reality --sensory input organised by patterns-- could be empty of theoretical constructs as conceptual stand-ins for them, but also some theoretical constructs --especially mathematical ones, but not necessarily just those-- could have no sensory-input counterpart for them. My hope for this possible fly in the ointment of our intellectual satisfaction is that the map could be completed with different patches, very much in the way that cartographers map geographical reality with different patches, and consistency rules for leaping from one to another. A map that faithfully represents regions around the equator, presents major distorsions of Antarctica.

Yes, exactly. While not impossible to conceive, thinking that photons emitted 3 bya by remote quasars somehow code the decisions that primates will take here and now on a particularly rainy day in Vienna at, say, 8:00 AM, is next-to-inconceivable. That the information be so intimately interwoven as to produce this next-to-hallucinogenic coincidental effect is something I don't want to even start to consider. I think the solution to the perplexing results of the quantum theory of measurement are better tackled by some kind of "fiduciary internal determinism." Something very much in the vein of what John Bell proposed with his beable idea. It would involve the idea that a choice of wave function does not determine everything. Infinitely many gauge descriptions would hide the "hidden variables." The catch is: Hidden variables are hidden forever, they never show up completely. They simply can't be seen, ever. There's a logical --and experimental-- fundamental obstruction. I think that's the way out for the problem of measurement, and I think that's the natural logical continuation of John Bell's musings. But that's probably the topic for another thread. That seems to be the case. I cannot wait for her to give up on that, because she is very much the conscience of theoretical physics today.

Sure. I'm sure most everything can be approached by algorithms. The missing part here would be the rotation properties of vector fields, but I'm sure that can be done too. That you're confusing the map for the territory. A map of the world is not the world.

An example is worth a thousand rules. Can you give one?

No. And @studiot is giving you the answer: A rock is made of something. A mathematical object doesn't have to be, because it's defined by logic. It's not made of any ingredients.

Thanks for the clarifications. +1 The "that would mean" kind of gives it away. I've been worried by this for some days now... Is Zeilinger endorsing superdeterminism??? I will get hold of this book and read the paragraphs in their natural logical flow, if you know what I mean. I did understand that the quasar experiment seems to rule out superdeterminism, though. But at that point it seemed to me that Zeilinger was considering superdeterminism as the only way out to save locality. That would be a big "oh, no!!" by me.

Sometimes you can look at the same fact from different perspectives... Example: In order to find its path from A, a particle follows the clue of velocity and force or, In order to go from A to B, a particle tries to minimise its action Both are mathematically equivalent.

Not all fields are scalar fields. You're implying scalar fields. Fields can be scalar, real, complex, tensor, spinor, vector... They can code fibres, curvature, torsion, topological numbers... Fields are abstractions, they don't have to be made of anything. They must comply with certain rules though.

Exactly. It's clarified in the next paragraphs. Zeilinger does not endorse "spooky action at a distance": (quoting Zeilinger.) The part highlighted in red seems to be implying superdeterminism. I would postpone that, because you have a dangerous tendency to mix up different topics. Suffice it to say that superdeterminism is just one loophole for someone who wants to save some kind of determinism at all costs. People who are familiar with mathematical proofs know very well that finding a counterexample does not necessarily imply the counterexample is unique. The part highlighted in boldface black is the most important one, which ratifies what @Eise is saying. Good. If you understand what you've said, you could be on the verge of understanding your own confusion. It's not a minor point. It's very important. It's the essence of the projection postulate, which is deeply non-local, but has no non-local consequences. Only problem: It's just a convention. It's not an evolution law for the state, and certainly not a law of physics. And most importantly, it has no experimental consequences. It was theoretically designed to do exactly that. Go back to my comment on FAPP's Bell's comment. Most physicists that contributed to the formulation of QM had no problem in seeing the state vector as just an epistemic book-keeping device, reflecting our knowledge. That's why they had no problem in introducing a non-local, non-unitary mathematical convention of which no non-local consequences could be derived. And last, but not least, as Eise has said above: No. Non-locality does not imply non-realism. They are very different assumptions. Example: Plane waves propagate in a totally local way. Yet, by virtue of selecting the momentum, the position is totally undetermined. That's local non-realism at its simplest, even before we start talking about entanglement. @bangstrom. You also said this in answer to @MigL: The quote is from Bohr, in answer to Einstein's famous "God does not play dice" --a colourful way of saying he didn't accept indeterminism at that point. But, really, is that "the explanation" of everything we're talking about here?

LOL. You've made a good point before, and something deep inside of me tells me you're about to understand an important part of this problem. Maybe tomorrow. Hint: You said "minor point." It's not minor at all. It's the key to all the confusion.

Here's a riddle for you: If there's no way to know which "action" came first --in a given frame of reference--, how do you know the time interval between the "actions" can be tagged as FTL?

Non-realism is just the character of QM. So it's not "we don't need it." It's what it's like. |electron> = |electron here> + |electron there> |vacuum> = |particle> + |antiparticle> Etc. It's what it is. A non-realistic theory out and out. OK? It's not "we don't need it" or "maybe tomorrow" or "I don't like it" or "we can do without." Well, maybe you don't need it, but it's what it is. That's factual. The double-slit experiment has no entanglement, and already tells you that much. I know you don't like my objections, but I'm here again.

(boldness by you, boldfacedness by me.) Exactly! Thank you.

No, it's not. It's actually a very quick and surprisingly deep understanding of the question, IMO, from someone that declares not to be all that familiar with the mathematical formalism. @Eise has understood this very clearly IMO. He's a very careful and attentive, and deep reader, and he has corrected me when I (wrongly) quoted Bell, when it really was Einstein quoted by Bell. It's you who, for some reason, keep saying that non-locality has been proven. After the last entry on my part, you've decided not to respond. You do this again and again. Mind you, the most dangerous thing concerning this topic is taking at face value what many people in a half-arsed way think they understand about it. You may end up wasting millions of SGD (Singapore Dollars) in declaring such stupid things as "oh, wow, my tardigrade got entangled with my qubit, how about that?" Silly, silly, stupid, mind-numbing nonsense "scientoids" --rather than science facts--, hyped to the max, totally void of content, expressed in a deliberately confusing and ambiguous language, and responsible in a big way for the bad image of science in the minds of many intelligent laypeople in this revolting, repugnant, post-truth age!

Disclaimer: I don't mean I endorse this view. In fact, it's shocking to me that someone like Einstein held any hopes that a classical theory of EM and gravity could some day explain spin, radiation spectra, particle spectra, etc. The very first time you see and understand commutation rules in QM, and the utterly fundamental role they play in it, it dawns on you: There's something here that no classical way of thinking can reproduce. I once read --it may have been on one of James Gleick's books-- that Einstein was presented with Feynman's brand-new path-integral formulation of QM by Oppenheimer, so as to intimidate him with the beauty of it. His answer was something to the effect of "Oh, I think I've earned my right to be wrong by now." If the story is true, Einstein was very much aware that he must have been left something out. Something essential. So no, in case there's any doubt, I do not endorse Einstein's view. But his argument about particle trajectories. Oh, be in no doubt; that still holds. Dear @bangstrom. Here, again:

Sure. Because Hoola said "to the degree I understand it", I felt I needed to avoid words like "a metrical property" which are more adecuate. This metrical property goes with the mod squared. Here. Again: There are many questions here that can be invoked in the same context: Completeness (where do "classical" data come from?) Indefiniteness (where were those "classical" data stored before the measurement?) Locality (do we need to introduce some kind of superluminal updating to implement "classical" data?) Counterfactuals (why are there measurements without interaction?) You could throw in more (contextuality, delayed-choice, etc.), but they're all related to each other. The quantum state holds the key to most of the "paradoxes," but you need to keep the character of QM in all of them. I told you, it's like a house of cards. If you remove randomness in a particular way --print something in the state, so to speak, and still use its built-in correlations-- you would be able to send FTL signals..., etc. Why did I talk about gloves? Was I endorsing Einstein's view? No, I wasn't. I introduced it the same reason that John Bell introduced Bertlmann's socks example: To show that in order to have perfect anti-correlation at a distance, you don't need any non-local mechanism going on. But no pair of gloves, boots, coins, astronauts, etc. can give you the other quantum correlations for spin: statistical variance of (A) = 1/2 statistical variance of (not A) = 1/2 statistical variance of (A+not A) = 0 statistical variance of (A+C) = statistical variance of (not A+C) = 1/2 for other C's incompatible with A, because classical observables don't have this character of incompatibility. A, B, and C are spin projections. Incompatibility comes from non-commutativity. If you listen carefully to Sidney Coleman's talk --or read the transcript--, this particular point becomes very clear, as well as how John V. Neumann understood this very clearly, and never got entangled in silly discussions about non-locality. How that endorses Einstein's view of realism, when Einstein spent the last 25-odd years of his life thinking about other things and not accepting QM, is beyond me. Einstein was concerned with trajectories of particles. Go back to the paper and tell me if he ever mentions spin. He doesn't. He never did. He didn't even accept lambda hyperons, and other elementary particles, because he thought somehow all these quantised features would some day be deduced from a unified theory of gravity and electromagnetism. Einstein was thinking about particle trajectories, nothing else. The lesser-known paper with Tolman and Podolsky, Knowledge of Past and Future in Quantum Mechanics, and others, prove that very clearly.

OK. I have a feeling I haven't been very helpful. Let me pick up on @MigL's observation that, Exactly right. These waves, among many other interesting properties, have one particular funny property: They have some kind of a "volume" that must be the same at all times. We call this law "unitarity." This "volume" is actually not ordinary volume. It has no dimensions, it must always add up to one, and we understand it as probability. The probability of all the alternatives of an experiment must add up to one. It makes sense. You cannot have a quantum wave become zero, even for a split second, because this "zero wave" would have "zero volume." So you can never have any physical process make the quantum wave shrink out of "existence," so to speak, even for the shortest period of time. Let me tell you something. Believe me, there's no "laughable" idea that you can think of which there isn't a similarly "laughable" idea I haven't thought of before, or MigL, or anyone of us. It's not laughable at all what you say. We know it doesn't work for the reasons I tried, to the best of my abilities, to explain. Very eminent physicists and mathematicians have ventured down really deep rabbit holes in order to try and explain these things. So bad it is that humanity lost very valuable people down those holes. Einstein is perhaps the best example. I think David Bohm was another one. But that's another story.

Another interesting application of complex numbers inspired by physics: Materials have a refractive index. The reflected wave is given in terms of the real part, the imaginary part conveniently embodies the property of absorbance. So a metal has a considerable imaginary part in its complex refractive index. This is a nice example of what @Markus Hanke said about complex numbers as exponents. I see nothing "imaginary" in the ability of a material to absorb light. Why wouldn't one want to use such a handy book-keeping device?

You cannot add wavefunctions corresponding to two particles. Superposition is only valid for states of the same system. The wave function of a two-particle quantum state cannot be arranged to add up to zero. In the formalism, this is reflected in that they are functions of different variables. Furthermore, you can never totally cancel a quantum state. The zero vector in the state space has no physical significance. The vacuum that we use in quantum field theory \( \left|0\right\rangle \), for example, is not the zero state vector. There is no zero state vector in quantum mechanics.