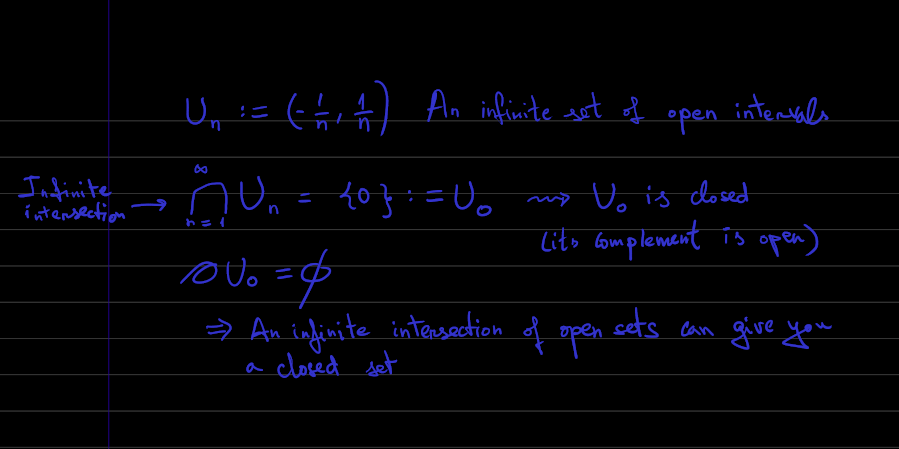joigus

Why would Jesus return verses? Because of spelling mistakes?

This is a brilliant point I was thinking about. Only laziness prevented me from ellaborating. OTOH, the collision seems to have been a head-on hit. A lot of collisions are at an angle. Examples are the Thea-Earth collision or the Chichxulub even. We seem to require a head-on collision at nearly zero relative velocity --otherwise we would be talking about a huge amount of debris flying off in all directions. Wildly different results depending on collision parameters. The Mercator projection heavily distorts anything close to the poles, and is more accurate near the equator, as I remember.

Christian rock. Thank God it was rock, and not elevator music.

No amount of thinking can ever beat a hotline to the gods. The line was busy, but after waiting for some hours, Jesus has told me that your argument including the uncertainty principle is quite robust.

I already made those points and you didn't bother to answer. What's the point?

Hold on, I've got Jesus on the phone, and he's telling me you got him completely wrong.

This is the problem. Some people take what really are dumbed-down verbalisations of salient aspects of physical theories, and run away with them. Add Jesus to the mix, and you've got this post. Energy could not possibly have been infinite at the big bang. I think you mean energy density. Energy = -infinity makes even less sense. Energy is positive definite, otherwise you have non-causal behaviour. x-posted with @Phi for All

No, no. It was just a slip. Certainly Curie's law I would call emergent, and by Curie's law I mean, https://en.wikipedia.org/wiki/Curie's_law But it has nothing to do with pressure. Magnetization is purely an average of microscopic fields, but how it relates to temperature (the law itself) has emergent features no doubt. But we were talking about pressure, and of course Curie's law has nothing to do with it. It was a 'Curiean slip'.

Indeed. And every minute I can think of more and more examples of why this 'idea' can't even get off the ground. But, Agreed.

(My emphasis.) OK. So to clarify further. I said, It sounded like I meant force is not present in the parts, but that's not what I meant. And, of course, that's not true. What I meant by 'pressure is not chunks of little pressure' is that it doesn't work like force, it has a qualitatively and quantitatively different law (in most cases it's not directional, it has an equation of state that relates it to other emergent variables, rather than Newton's vector or Lagrange multi-variable equations of motion.) It's related to temperature, which is clearly emergent, or highly-derived, if you wish. It's not the same as, e.g., the macroscopic version of Maxwell's equations, which are essentially the same. If you take the properties of matter into consideration, you do have to introduce de D, H fields to complement the E, B fields, by including $\varepsilon$, $\mu$, but the equations are pretty much the same. Now, the way I understand it, the latter is definitely not emergence, but just averaging. Although some people might argue that in some sense it is.

Sorry, that's nothing to do with pressure. Mistake.

This is hands down one of the silliest ideas I've ever heard. Just to add a couple more to what Studiot already said: What about nicely-deposited billions-year-old sedimentary rocks, and surfaces of rock with the unmistakable fingerprint of ancient tides and water waves? What about the perfectly-preserved fossils (billions of y.o.) of stromatolites? How did they survive the crash? Do you have any idea of the range of collision velocities for astronomical bodies?

Myriads of directional vectors have as only effect, to all intents and purposes, just one scalar value. These forces are directional; pressure is a scalar. These forces are wildly time-varying; pressure is constant or smoothly-varying. Etc. OTOH: When a system of the order 1024 variables can be effectively handled with 3 variables for all that matters, I call that 'emergence'. This pressure satisfies qualitatively different laws that cannot be thought of directly in terms of Newton's laws. It satisfies different laws, like the Van der Waals law, or the ideal-gas, the Curie law or any other equation of state. So it's not the same, it doesn't behave the same way, and it cannot be described in similar mathematical terms. I see your point that there is kinda like a microscopic version of pressure, but I think that laws that go with it are an important criterion when it comes to judge when some quantity is emergent. In any case, it's a matter of defining a boundary.

Very interesting points are cropping up. Later, I would like to have a go at @StringJunky's example of a wave as an example, perhaps, of something we don't tend to think of* as 'emergent', but it really satisfies the essential criteria. Also, I would like to have a go at @TheVat's mention of Lee Smolin's efforts to realise space-time as 'emergent'. This, IMO, would require to construct space-time, as built up of more elementary building blocks, which might just be a matter of the description --see below. But now I would like to contribute the following observation. Sometimes emergence appears as a result of correlation: 1) StringJunky's Mexican wave (many elements and strict correlation in behaviour) But sometimes not: 2) Ideal gas: Pressure, temperature, and a host of thermodynamic variables, are relevant precisely because the particles are non-correlated in their behaviour (actually, completely non-correlated). $$\left\langle x_{i}x_{j}\right\rangle =0$$ $$\left\langle p_{i}p_{j}\right\rangle =0$$ In this case,** it is precisely because the individual dynamical variables are completely uncorrelated (statistically flattened-out, so to speak), that we can talk about the system in terms of variables that do not bear any relationship whatsoever with the microstates. It is entirely possible that this question of emergence is one that has to do with the description we wish to do --or find ourselves bound to do for practical reasons-- than with any condition that the system imposes upon us. *This is possibly because the wave equation in terms of differential calculus was worked out by some of the Bernouilli's mathematicians so long ago, when the concept of 'emergence' was not in the toolkit of scientists. **Now that I think about it, this is a very special case of correlation --very much in the vein of what Hanke said before.

IMO, and as @studiot very shrewdly pointed out, having however many elements is not a sine qua non in order to have a pattern of behaviour that merits the name of emergent. You could have just a pair of 'particles' and see something appear that is not qualitatively equivalent to the addition/yuxtaposition of the parts (potential energy, entanglement,...). Quite simply, it's not present there when you consider a situation in which the elements are isolated (non-interacting, non-correlated,...) with high enough accuracy. Your example that terms like dark energy in the Einstein equations were to be 'collaboratively caused', so to speak, is a distinct possibility, the way I see it. Of course, you would need a suitable set of hypotheses to show how this could be done. But I see no reason why something like this could not be achieved, in principle. Within that (hypothetical) theoretical framework, it's possible to conceive that a model with just 1000 galaxies could give you some kind of crude picture of a cosmological constant. OTOH: If the level at which an idea like that is articulated were not to be that of galaxies, but stars, and if that many stars is conceived as a logical necessity, 1011 galaxies, each equipped with 1011 stars really make a big bunch of them. That would make an overall number of stars of 1022 stars within a cosmic horizon which is, now that I think about it, nearly an Avogadro's number worth of galaxies. So I guess what I'm saying is, why not?

It already did in 1992, when I first listened to it.

🤣 Humpback whales should be sounded out on this too. And as to cooking, I don't know, but a fusilli version of Dark Side of the Moon seems interesting.

Interesting. I wonder if you would need some kind of wave guides to keep that going. The resonators that produce it seem to be very special, and I'm not sure that once the waves are on the air the vortices would be maintained. But sounds good, and sorry for the lame pun. As to applications, I simply don't know, besides the obvious: More degrees of freedom imply that more information could be carried by the wave.

Very good points. Your point No. 2) and 3) Let me add another example from topology: An infinite instersection of open set doesn't necessarily give you an open set. Example (for those mathematically-minded): So by making so-called transcendent operations (performed in infinitely many elementary steps) you can lose even the most common-sense properties that you would think should be preserved. Intermediate case between your points 2)/3) and your points 4)/5) (kind of what @exchemist is talking about: The key, IMO: You don't need infinitely many elements to have emergent behaviour. A large enough number could be enough. E.g. In statistical mechanics we know that when your system has a finite number of entities, but big enough that the Stirling approximation holds: lnn!≃nlnn−n Then the Maxwell-Boltzmann distribution, and describing the system in terms of thermodynamic equilibrium is on safe grounds. So you can describe the system with far fewer variables than it fundamentally has. Your points 4) and 5) are very similar in that: In some cases, you don't need the number of variables to be especially large in any sense. Your examples of potential energy, and the bricks necessary to make an arch, or a corbelled roof, don't really require big numbers. Another example similar to your potential-energy one is entanglement of two particles. As to your point 1) I don't think we're talking about the same concept of emergence there. Although the words are the same, that's more like what I would call*, morphing, mutation. A right choice of word would be needed to distinguish them, but it's not the same. The one you propose is more about causal emergence, IMO. *'Evolution' would be another possibility, but liable to be confused with 'evolution by natural selection' which is another kind of emergence. EDIT: I didn't see you were already talking about entanglement.

--StringJunky From:

That's a brilliant point. And kind of the direction I was trying to go when I pointed out on the thread about emergence that some apparently indisputably emergent concepts later appear as seemingly fundamental in another part of the theory, as if there was a POV-dependence that you cannot get rid of. I think this comment should be quoted in the other thread.

Since very early on I've thought Nature is superior to art (a little Socratic trick, as art is produced by humans, who are produced by Nature). Hands down it is. After all, she's had billions of years as a head start on whatever part of it we call art.

The way I understand it is like this: A phenomenon is emergent when it can be studied in terms of elementary parts and their relationships, while the phenomena to be explained are not present in the parts, appearing instead as a consequence of certain relationships between them. The example par excellence is pressure, which appears as a result of miriads of molecules hitting the walls of the container in so smooth and regular a way that all we experience is a consistent and continuously-varying resistance to reduce their volume if we try to push the system into a smaller volume. The idea that spacetime may ultimately be emergent appeared in physics in recent decades, in the form of commentary, rather than an actual proposal, I think. There are attempts to go in this direction, like loop quantum gravity, but I don't think it's any close to come to fruition. I quite agree with @studiot in that a standing difficulty, at least for me, is: What is the more fundamental thing of which time is a derived (another word for 'emergent') concept? Some people seem to think that considering time as made up of little chunks, discrete, is the big idea. Now, that's not how the concepts of pressure or temperature were arrived at. Pressure is not chunks of little pressure; temperature is not chunks of little temperature. Another problem I see is that sometimes we think we've understood a concept as emergent, or derived, only to find later a version of it that seems to resist such, shall we say, reductionistic approach. Examples of this are, IMO: 1) Negative pressure of the cosmological vacuum 2) Pressure and temperature* in black holes I don't think these can be considered just your garden-variety versions of pressure and temperature amenable to be understood in terms of 'little things doing their thing.' But who knows. All I can say for now is that it seems to me that any concept of emergent time that emerges (pun inevitable) is bound to be essentially different from being so in the same vein of temperature and pressure, ie, as 'little things doing their thing.' Something very really bold and beautiful seems necessary. I'm particularly interested in what @Eise and @Markus Hanke have to say about these matters. *Temperature is not just a feature of black holes, but also of any space-time horizons; even** horizons created by just picking a coordinate system (Rindler coordinates for flat spacetime). What about that?! **Not a typo for 'event'

It seems to be a semiclassical calculation, in which they've thrown in elements of quantum information theory. It's always a good thing that you can get confirmation of robust physical principles from approximate pictures of the physics. Thanks a lot.