joigus

No, that must have been before I 1st came here. Teaching methods interest me a lot.

Lame joke on my part. I know how much you love books. You actually mentioned the human factor. I couldn't agree more.

No. You need to say what these things are.

Wonderful complement to what I was saying

Now I know @studiot is going to hit me hard. What I mean is: Look out for teachers that are putting out their material online, a lot of them for free. When the drive to learn synchs with the drive to teach, something wonderful happens, and knowledge is passed on. If the teacher does well, and the student does well, elements of criticism and analysis of how ideas are built and corrected/improved are also transferred in the process. Khan Academy --that @Phi for All already mentioned--, Stanford, MIT courseware, and a long etc. You've got plenty of university material out there. And my all-time favourite, PI (Perimeter Institute): Psi Online

Probably just a rhetorical question, but interesting nonetheless. The answer, very much having to do with the excellent points made, is all about symmetry groups --from a mathematical physics perspective. In economics, eg., you have graphs representing marginal utility --dimensionless, if I remember correctly-- plotted against number of units of goods --again, dimensionless. In electrical engineering tho, you have graphs plotting intensity against voltage --both dimensionful. But the subtle mathematical point is that in neither of those cases is there a group of symmetry relating different, but equaly valid, observational stances --classes of valid observers. In the physics of space-time, there is such class of valid observations, and the measurements of time and space of one observer are mixed up with the measurements of time and space of another, so it is natural to define the parameters of the transformation as dimensionless numbers. You could insist that (I,V) (intensity and voltage) be a 'vector', but it doesn't make much sense unless you can define transformations that take one stance to another and relate them in a linear way: I'=aI+bV V'=cI+dV with a,b,c,d being the dimensionless parameters that mix them up. That's the reason why in mathematical physics you tend to be more careful and say: Such and such quantities are a vector under SO(3) (rotations); or a vector under O(3) (rotations and inversions-reflections), etc. In the case of Minkowski vectors, it's all about inertial observers. It's what we call the 'Lorentz group'.

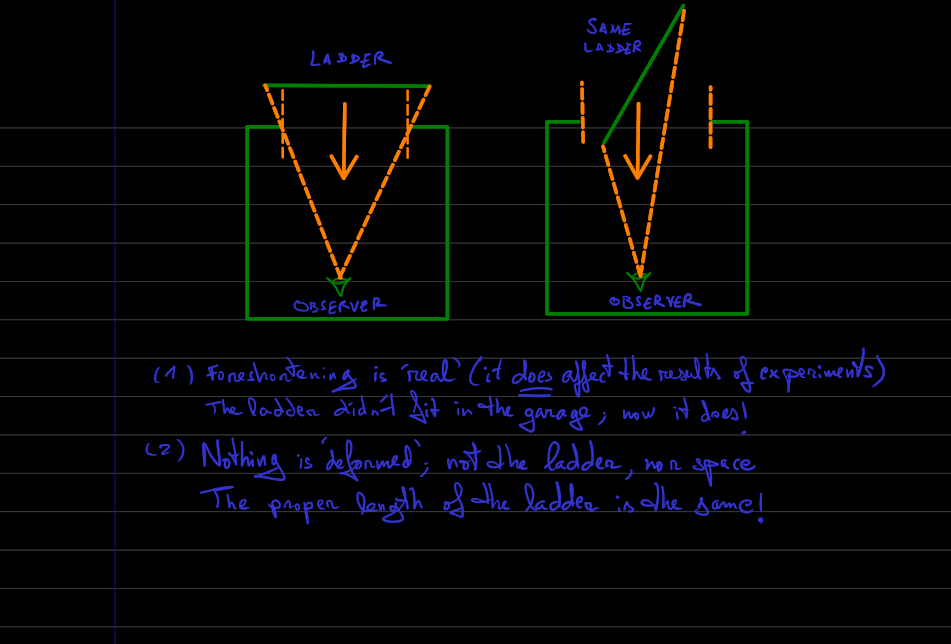
Ok. I'm sorry if I missed a particularly subtle point you made. The OP seems to be under the impression that special relativity demands us to admit that space 'deforms'. I was just trying to be helpful, because I think that's an unfortunate misconception. (my emphasis.) Wrong!!! That's what I'm trying to address. And believe me, we've all been there at some point. Even though I'm under heavy workload, believe me; I wanna be helpful. So I've made a little drawing that explains why that's wrong based on my analogy with foreshortening in space. Nothing is deformed. Space is not deformed. The object is not deformed. Yet, foreshortening is real enough that, if you don't take it into account, you're going to damage the paint from the frame of your garage's door, and the ladder, or worse. The explanation that special relativity gives of this is just common sense. Common sense gets you a long way. One must study special relativity and there comes a moment when you naturally understand it, and there's no looking back. That's what I meant.

Gladly, Studiot. Thank you for your interest. Here's a couple of comments from yours truly that deal on this same comparison:

An elementary particle has just one worldline, never a bunch. Unless you're considering something in the way of Feynman's path-integral approach to quantum mechanics, in which a particle 'feels around' for possible paths with its wave function. Is that what you mean, @34student? On the other hand, even from the classical point of view, an elementary particle can be considered to have a bunch of field lines (infinitely many) coming from the particle. I'm not sure what the OP really means, but I think it would save everybody a lot of time if they clarified what they mean. (Emphasis marking up literal expressions in OP that could be relevant.) Just another observation: In physics, worldlines (or worldsheets, in string theory) don't necessarily represent observers. They are theoretical constructs to represent classical histories. Feel free to keep ignoring my attempts to clarify the question.

Minkowski space-time does not need a fundamental re-think. The reason why is the very same reason why understanding foreshortening of an object's length when one's holding it in a peculiar position doesn't need a fundamental re-think. It requires us to understand the laws of perspective and observer dependence of measured quantities. Lorentz-Fitzgerald scaling laws are laws of forshortening in space-time, just because going from one inertial reference system to another is like rotating in space-time. Simple as that. Simple is one thing, easy to accomodate in daily-life intuitions is quite another. A very different thing would be asking where space-time itself comes from, why 1+3 dimensions, what the limits of validity of pseudo-Euclidean geometry, or Einstein's GR. But not the build-up of how these laws apply in the ordinary range of validity in distances, energies, times, etc.

Extraordinary talent requires extraordinary self-criticism?

Early quantum theory departed from the idea that energy states of particles in a confined space had to do with wave modes in that confined space (think of a box). Those wave modes are quantized in energy (and therefore in momentum, for free particles) when these waves are in a perfectly reflecting box. It took some time to realise that this could be formulated as due to the fact that matter, in all its forms, has a wave-like nature to it. The particular hypothesis that answers your question is due to De Broglie. Following De Broglie, a monochromatic wave of wavelength \( \lambda \) has a momentum (think just one possible direction), \[ p=\frac{h}{\lambda} \] Think also of free particles. Now, because a harmonic wave of wavelength \( \lambda \) and time period \( T \) is represented by, \[ \psi\left(x,t\right)=A\cos\left(2\pi\left(\frac{x}{\lambda}-\frac{t}{T}\right)\right) \] and as Studiot said, your “nabla” (derivatives, one for every direction, that in this case is just one, \( x \) ) have to act (differentiate) on this something (the wave), \[ \frac{h}{2\pi i}\frac{\partial}{\partial x}\psi\left(x,t\right)=2\pi\frac{h}{2\pi i}\frac{1}{\lambda}\sin\left(2\pi\left(\frac{x}{\lambda}-\frac{t}{T}\right)\right)=\frac{1}{i}\frac{h}{\lambda}\sin\left(2\pi\left(\frac{x}{\lambda}-\frac{t}{T}\right)\right) \] Now, it just so happens that in quantum mechanics you must complete the so-called wave function so that it has an imaginary part. This imaginary part (for the complex-number version of a monochromatic wave) is, \[ i\sin\left(2\pi\left(\frac{x}{\lambda}-\frac{t}{T}\right)\right) \] The whole simplest version of this 'wave function' would be, \[ \psi\left(x,t\right)=A\cos\left(2\pi\left(\frac{x}{\lambda}-\frac{t}{T}\right)\right)+i\sin\left(2\pi\left(\frac{x}{\lambda}-\frac{t}{T}\right)\right) \] Repeating the previous process for the whole complex (real plus imaginary parts) leads to, \[ \frac{h}{2\pi i}\frac{\partial}{\partial x}\psi\left(x,t\right)=2\pi\frac{h}{2\pi i}\frac{1}{\lambda}\sin\left(2\pi\left(\frac{x}{\lambda}-\frac{t}{T}\right)\right)=\frac{1}{i}\frac{h}{\lambda}i\psi\left(x,t\right)=\frac{h}{\lambda}\psi\left(x,t\right) \] So that's what your momentum operator does on states. \( \psi \) is called 'state of a quantum system' or 'wave function'; and the things to measure (momentum) are mathematical operators that extract this information from the state. I hope that was helpful.

This is dedicated to @Moontanman. What's become of you, bro?

Just skimming through this. I don't want to encourage the OP to pursue what essentially looks like a fundamental confusion between 'world line' and 'field lines' à la Faraday. But I agree that that's a good question. Although unfortunately belongs in a different category and I don't think any of us has a ready answer to it.

I've been known to act like a cretin, but I'm certainly no Cretan.

Parity is always well defined for any particle or system of particles. OTOH, parity is an involution. This means that if you apply it twice, the state goes back to itself. This, in turn, implies that quantum mechanical particle states can be either even or odd under parity, and nothing else. Given that parity is not conserved in Nature (not even parity, but parity as such), the final state could have but even or odd character under parity, but both are OK. I cannot be sure of what your mental framework is, or your level of acquaintance with the principles of quantum mechanics, but remember that several particles (think decay products) are not a sum of individual particle states, but a product. I have a feeling that's what's bothering you. Is it?

It seems that only @Ken Fabian mentioned comedy. Here's an (allegedly) underrated classic: https://en.wikipedia.org/wiki/Quark_(TV_series)

Here's the quote: https://books.google.es/books?id=jJzGNl9K5SIC&pg=PA277&lpg=PA277&dq=murray+gell-mann+"close+to+a+proof"&source=bl&ots=Wsndi_9ZiJ&sig=ACfU3U1TVvvcpwOmBDk1GxpNphUqSMmSdQ&hl=en&sa=X&ved=2ahUKEwjNxeDZ-pL0AhVoBGMBHWRADHMQ6AF6BAgCEAM#v=onepage&q=murray gell-mann "close to a proof"&f=false https://www.worldscientific.com/worldscibooks/10.1142/7101 Article: Particle Theory, from S-Matrix to Quarks The quote is: (My emphasis.)

Simple and enlightening.

I would say these are problems for so-called numerical relativity; that is, numerical simulations with Einstein's equations, and parametrizing the collision data. I'd think impact parameter and velocities of approach, masses, and so on. I've found a reports-like paper that could be what you're looking for. https://arxiv.org/pdf/1909.06085.pdf I hope it lives up to your expectations. Haven't had time but to skim through it a little bit.

I'm proud of you, young man. I wish I could give you 5 reputation points for this. You didn't just believe me, and went on and performed the experiment. I could have been lying to you.

Ah. Seems like by groping in this relative darkness, you've come up with a very interesting question. I'll let Andrew Wiles do the talking, because I think he's got something to say that's related to your question: [Quoted from Did earlier thoughts inspire Grothendieck? by Frans Oort, who refers to the BBC documentary by S. Singh and John Lynch: Fermat’s Last Theorem. Horizon, BBC 1996.] [With thanks to Thomas Riepe] Taken from: https://micromath.wordpress.com/2011/11/06/andrew-wiles-on-doing-mathematics/ I'd read this quote before as referred to number theory, which Collatz's conjecture is really about. The idea is that you could be microns away from the switch and you wouldn't know. So I'm very skeptic of any relevance of any statement on how close you are to a proof of something. Seems like something that cannot be graded. But that's my feel of it. I have a heartfelt love for pure mathematics, but I don't have the training of a pure mathematician. Taking up from Wiles' metaphore, I'd ask: Is there a way to judge whether the switch is within your reach before you've touched it? I know I'm waxing metaphorical only, but I think you perfectly understand what I mean. I remember the late Murray Gell'Mann making similar comments on some 'mathematical people' saying they were 'close to a proof'.

Interesting... By definition, any conjecture that stands unproven is beyond the reach of present day mathematics. So Erdos is being kind of tautological, whether on purpose or not, I don't know. And as to the second sentence, you're comparing two unponderables: 1) The time it will take humans to solve Collatz's conjecture 2) The time it will take humans to get nuclear fusion to be practical ('practical' = ?) I'd say there's no answer to your question ('I wonder...'). Unless 'there's no answer to your question' is considered to be an answer to your question'. And that, assuming you're asking a question --maybe you're just projecting a wondering.

So how do the EM fields generated by the apparatus exactly cancel the interference pattern? A little bit of maths would help someone like me. I like your line of thinking, but a line of thinking doesn't make a theory. The idea that electrons are somehow both particles and waves, as embodied by standard quantum mechanics, is far superior in that it correctly predicts all properties that we know about so-called elementary particles. Plus, Your theory --once it's formulated in a mathematical fashion-- should be able to explain such other phenomena as those implied in the Aharonov-Bohm effect (a 360º rotation of the electron completely 'inverts' its state). Now, that is weird in terms of EM alone; EM fields do not explain it. One double-slit doesn't make quantum mechanics. QM goes much deeper. It ushers in a whole new way of thinking about physics.

Sorry, I meant "aluminum foil". I'm an old person, you see. Plus my vocabulary is somewhat out of whack due to age, language acquisition, and random influences. The important thing is doing the experiment. It's a very simple experiment, anybody can do it; and it illustrates perfectly Faraday's cage to shield from EM waves that Swansont was talking about.