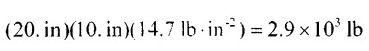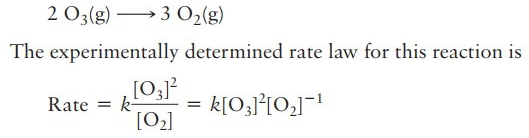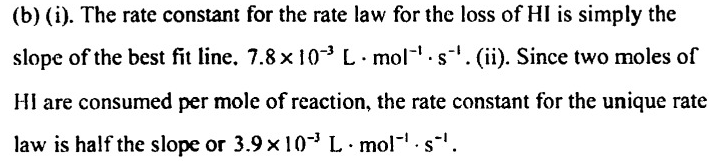Scienc

I realized that the mistake I made was a technical one, and not related to the issue at hand. My assumption of using Newton's second law would only make sense if the pressure unit was in Pa or N/m^2. However, since the pressure value was given in lbf/in2, the value obtained by multiplying the area with P (in lbf/in2) is numerically equal to the mass value. The response was a bit unclear, but it should have been understandable. As you pointed out, the weight of one pound is equivalent to one lbf here on earth. Therefore, if they wanted to clarify this, they could have done a conversion using the conversion factor of 1. However, this conversion should be understood even if it is not explicitly mentioned.

Thanks.

My colleague said that if you know how many square inches there are, you can determine how many pounds are up there based on how many pounds are in each square inch, and it can be obtained by multiplying: area*p But again, for me, the value obtained is in force unit and not in massa unit. What am I not understanding?

Thank you so much.

Guys, why in this question did the question answer only perform the product between area*P to calculate the mass? Question: Answer: Shouldn't the mass be calculated as m = (P*A)/g? Considering that: P = F/A, since: F = m*g P = (m*g)/A P*A = (m*g) m = (P*A)/g By performing dimensional analysis, you can indeed arrive at the value and unit: 2900 lb. However, I don't understand why gravity wasn't considered.

Can someone give me a hint on how can I prove it?

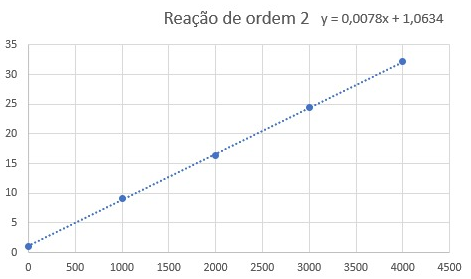
I have a question about the value obtained by Rate Law. For example, in this case: the value of rate obtained by this equation is the global rate of reaction, right, and not the rate of a specific specie, I know that using this global rate I can find the species rate, multiplying for his stoichiometric numbers. Is my assumption correct? Because if the answer is YES, this question no make sense for me. I was trying to solve this question: I created this graph (Title is in Portuguese): I used "1/[HI] x t," which indicates a second-order reaction with a rate law equal V = k[HI]^2, so, the slope of the graph is numeric equal for k, AND, if my previous assumption is correct, the value obtained for V is the global rate reaction, as a consequence, the constant (k) 0.0078 (L.mol-1s-1) represent the unique rate law and not of specific reactant (HI). However, the gab, says that 0.0078 represents the rate constant (K) for the HI For me, it makes no sense, because, if it is correct, the value of V obtained by rate laws is the rate of HI and not for the global reaction since k refers to him and not for the global reaction.

Thanks. Thank so much,

I am a beginner in QE and I have a question. During I was reading about Output file, I saw a part where have it: "The calculation goes on step by step until convergence is reached. Then we show all the energies of all bands (eigenvalues of the Kohn-Shan orbitals) for each k-point, the Fermi energy, the total energy, the contributions of all the terms to the total energy, and the calculation time used by each subroutine of the program." Output file: ... iteration # 9 ecut= 100.00 Ry beta=0.70 Davidson diagonalization with overlap ethr = 1.00E-13, avg # of iterations = 1.0 negative rho (up, down): 1.151E-06 0.000E+00 total cpu time spent up to now is 28.4 secs End of self-consistent calculation k = 0.0000 0.0000 0.0000 ( 3909 PWs) bands (ev): -17.8569 -5.9595 -1.3957 -1.3957 4.4242 9.2594 9.9561 9.9561 k = 0.0000 0.0550 0.0000 ( 3909 PWs) bands (ev): -17.8034 -5.8955 -1.6155 -1.5115 4.4968 9.3266 9.9837 10.1886 ... -10.9411 -10.9411 -8.9101 1.6562 1.6562 12.4084 14.2298 14.2298 the Fermi energy is 1.6562 ev ! total energy = -22.80493136 Ry Harris-Foulkes estimate = -22.80493136 Ry estimated scf accuracy < 1.5E-15 Ry The total energy is the sum of the following terms: one-electron contribution = -44.02527202 Ry hartree contribution = 24.36506286 Ry xc contribution = -6.99363523 Ry ewald contribution = 3.85762303 Ry Dispersion Correction = -0.00870488 Ry smearing contrib. (-TS) = -0.00000512 Ry convergence has been achieved in 9 iterations Writing output data file grafeno.save init_run : 2.26s CPU 2.29s WALL ( 1 calls) electrons : 20.10s CPU 20.24s WALL ( 1 calls) ... Parallel routines fft_scatter : 4.35s CPU 4.44s WALL ( 23020 calls) PWSCF : 28.46s CPU 28.70s WALL This run was terminated on: 11:51: 0 5Sep2017 =------------------------------------------------------------------------------= JOB DONE. =------------------------------------------------------------------------------=

So, is the true value for work +22, because work is done on the system? I used the 𐤃U = q+w. because I studied in a chemical class. However, I considered the contribution to work as negative. The book on the other hand, used a positive signal for work. The images is from the book.

I have a question about the resolution of this exercise: I tried to solve this problem with the following steps: For the 1º law of thermodynamics, 𐤃U = q+w. As q = 𐤃H at constant pressure, I assumed that in this process q = - 15 kJ. As a result, 𐤃U = -15 - 22 (because was an expansion) and for this reason, 𐤃U = -37 kJ. However, the book has this resolution I understood why the book used this method, but I did not understand why my method is wrong.

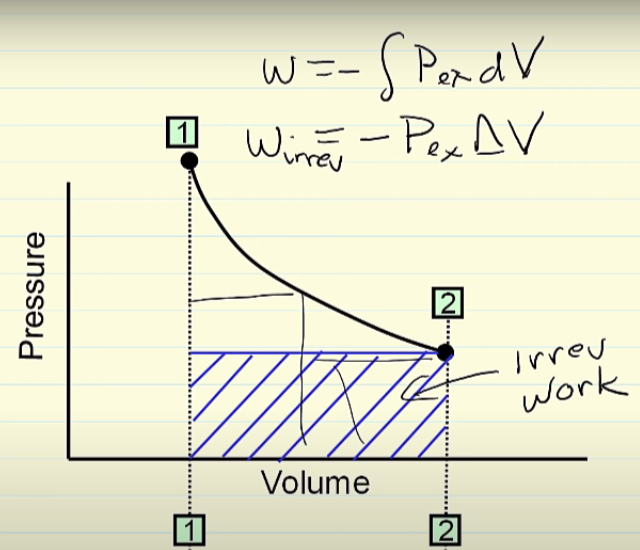
Why in an irreversible process, is the pressure constant? I understood why I should use Wirrev = -PΔV, but I did not understand why the pressure is constant in this process.

Why does CH3CO2H have a greater nucleophilicity than CH3OH?

An orbital can contain up to 2 electrons, and the electrons and orbitals are described by wave functions, are the 3 wave functions the same? for example, two electrons that are in the psi 2 0 0 orbital do they have the same wave function as that orbital?

What does "air is saturated with water" or "air is saturated with something" and how can I relate this to vapor pressure?

What is the physical meaning of enthalpy?

The volume that 6 moles occupy 134.4l and 12 moles occupy 268.8 moles, since 1 mol = 22.4l, for this the gas needs to expand

What is the difference between the work done by a gas and the workflow that the same gas performs to exist? why does the variation in the internal energy of the equation dH = dQ + nRT not consider the work done by the gas to exist (working flow) but consumes only the heat transfer? In the question below, the author considers dU = Q. He performs the calculation of the work done by the gas, separated from the internal energy (with an equation dH = dU + nRT ). If you know that in systems with constant volume dU = Q, but the gas volume varies (From 6 moles to 12 moles of gas), this does not imply an internal energy variation equal to dU = w + q (As stated in the 1st law of thermodynamics) and why consider dU = w + q and not dU = Q **? In practice or in what he did, the logic he did not use was. Question: “A constant volume calorimeter showed that the fuel loss in burning 1 mole of glucose is equal to -2559kJ in 298K, that is dU = -2555KJ”

Thank you. Thank you.

A variation of enthalpy at constant pressure is numerically equal to the variation of heat in a chemical reaction, but what is enthalpy in itself? what is its difference for internal energy, is it calculated as H = U + PV, or does that mean physically?

Guys, why in physics does the work done by the system have the POSITIVE sign, but in chemistry does the work done by the system have the NEGATIVE sign?

Why does the equation τ = -n.R.T.ln⁡ (v_2 / v_1) only work for reversible processes?