Matthew99

Thanks for all the inputs so far! You are right. The more photons there are, the more transitions are induced and the probability of an electron for an up or down transition is the same. Thus, my initial argument of zero recombination is nonsense. May I raise on last (maybe dumb) question: In a semiconductor with a band gap of 2eV, how is it possible to emit photons of <2eV which are required for a blackbody spectrum? Is it because there are many different energy levels available near to the surface due to surface effects (loose or different bonds)?

Omitting reflection isn't physically permitted, is it? But if as you say recombination is inevitable, this could be a real fundamental limiting factor. Do you know if radiative recombination probability of one electron is influenced by temperature or if the reason for higher radiative recombination at higher temperatures is higher population of higher energy levels? Is this radiative recombination the reason for thermal radiation? Sorry if that is a dumb question, I've never thought about this in that way as this exceeds my working field which is in engineering. You are right, cell at 0K is a contradiction in itself. However, this thought confuses me a bit. Will this mean that every excitation of an electron increases the temperature of the cell, without having phonons involved?

I had in mind that if you had a hypothetical cell with zero resistance, an infinitesimally small voltage difference would be enough to drive the photo-generated current. You could theoretically use an ideal spectral splitter and direct each photon to a separate cell with the corresponding band gap. Please keep in mind that I am not talking about practical feasibility, I just want to find out if there is an inherent physical limit that prohibits such a device with 100% conversion efficiency as there is in thermodynamic cycles with the carnot limit. Now just because the physical upper limit might be a certain figure this does not say anything about technical feasibility. I just want to find out how much is possible without violating any fundamental physical laws. Would this also be the case if the cell were at 0K? The cell should not emit radiation at this temperature so doesn't this exclude each other?

Wouldn't this happen in any case? Due to thermalization, the kinetic energy that electrons have when they are excited up a band gap of 1.8eV upon absorbing a 2eV photon (->2eV KE left) would dissipate almost immediately AFAIK and the electron settles down to the CB edge - so there is no difference to being excited by a 1.8eV photon for the electron So it is physically impossible to completely omit recombination?

In practice, of course not. However, is there a fundamental law of physics forbidding a 100% conversion efficiency of monochromatic light? (as you mention that it could be treated as work) Aha 💡 This could be the solution to why the proposed device is impossible. Will this always be the case? For example, is it physically impossible to shine 1.8 eV photons at a semiconductor with a band gap of 1.8 eV and 100% absorptivity and solely generate electron hole pairs? It seems I didn't make it clear enough what I meant by "holding at temperature". In no way I meant that the cold object (solar cell) does not radiate heat off, of course it does. However, if this imaginary device could turn all incident radiation into work and discharge it to an external circuit, it would not be heated by the hot emitter. Now, as the device itself emits radiation, it would cool down. But as it is in perfect contact with its surroundings, it will "be held at temperature" by its surroundings. Nevertheless, as I am not arguing that this device is possible, this objection is meaningless. As to the workfunction & threshold frequency @studiot mentioned: To what extent is this applicable to this problem? Wikipedia says: " in a semiconductor the minimum photon energy would actually correspond to the valence band edge rather than work function". Thus, if you had a material comprised of infinitely many semiconductors with infinitely many band gaps, you have a band gap for every photon and therefore no threshold frequency, do you?

Thank you first of all for the new inputs. Before addressing them, I'd like to be certain that we are agreeing on these points: The imaginary solar cell I described in my opening statement is physically impossible If it would be possible, it would not heat up from irradiation as it converts the incoming radiative energy into external work Secondly, did l understand @swansont correctly that your suggest turning 1kW of solar radiation into 1kW of electricity is physically impossible, because solar radiation must be referred to as heat, leading to a thermodynamic limit turning 1kW of monochromatic radiation into 1kW of electricity is physically possible ? Originally, I assumed that the cell would be placed on earths surface, in perfect contact with its surrounding which holds it at temperature. Sorry for using ambiguous language - what I meant by efficiency is energy conversion efficiency - electrical energy out divided by radiative energy in Wouldn't 100% absorbtivity lead to every photon producing an electron hole pair in the mentioned ideal cell and thus lead to a 100% energy conversion? This is of course true for real solar cells / objects. But what if you have a theoretical cell which has a band gap for every frequency? That is why there is a Physics Quantity known as 'the work function'. https://en.wikipedia.org/wiki/Work_function This is also linked to what is known as the threshold frequency, below which any radiation from the emitter could not generate electricity. And we have already noted that Thermodynamics requires some of these lower frequencies to be present. https://www.electrical4u.com/work-function/ I'll have a closer look at this later

Sorry, I used a wrong word - I meant net energy flow in terms of radiation. This was an unwise statement as I do not believe that the proposed cell is possible, I just wanted to point out that if it would be possible that this statement would be true. This is exactly what I wanted to claim in the first place to support the thought experiment I proposed. Sorry if I was unclear. Radiation from the sun cannot be turned into work with 100% efficiency and thermodynamic limits do apply. Judging from that statement, I assumed you wanted to suggest that a 100% efficient solar cell does not violate the laws of thermodynamics. Of course, real objects placed in the sun will heat up. However, this imaginary solar cell I was proposing would not do that if this device were possible, wouldn't it? Are you absolutely sure on that? I've heard that merging of low energy photons to high energy photons is possible, AFAIK people have been working on that in the past for solar cells - so there is no law of physics preventing me from merging the whole solar spectrum into one wavelength, is there? If not, then where does the photon entropy go?

I am not negotiating this in any way. However, just because there is a net heat flow from the sun / 1000K object to the cell does not necessitate latter one increasing in temperature if I take out all incoming energy as work and power for example a battery behind the cell. Even though I never mentioned that the cell is in direct contact with the sun / 1000K object, I assumed that this would be self-evident from a) my description of the setup and b) the fact that we are talking about solar cells.

No it is not. As I mentioned in my last post, I don't see a working fluid being recycled in this setup, therefore the traditional approach treating it as a thermodynamic cycle might be faulty. I grant you that. As I said in my first post I assume that every incident photon excites an electron from the VB to the CB. This energy is then utilized in an external circuit. As there is no recombination of electron hole pairs and every photon "transmits" its energy to the outer circuit, what exactly is heating the cell? I never claimed the opposite. Every absorbed photon is utilized as electric energy. Due to T_Cell = 300K > 0K it will emit radiation, which is why it would cool down if there is no surrounding, but lets assume the cell is placed on earth and T_Cell is constant at T_Cell=T_surrounding = 300K. In my opening post I said: In my improvised model, I mentioned "work in outer circuit" (right hand side) Could you further elaborate on what you mean by that? I do not see why the argument I am advocating for, which is that it is physically impossible to convert radiation to 100% work, is irrational.

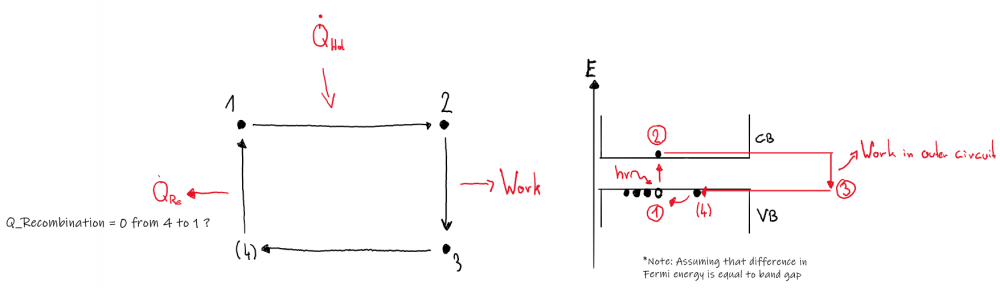
Maybe it might not be useful to use language derived from thermodynamic working cycles, as there is no traditional working fluid which is "recycled" after the extraction of exergy involved. However: As the energy input stream is not "pure exergy" but degraded due to carrying entropy, it should not be physically possible to produce 1kW of electrical power (pure exergy) from 1kW radiation. I just found a paper supporting this argument: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwjFnuqv39ryAhVZPewKHcX3AVkQFnoECBQQAQ&url=https%3A%2F%2Fnanohub.org%2Fgroups%2Fetsc%2FFile%3A%2Fuploads%2F4_part-1.pdf&usg=AOvVaw0kkzS5W5CG2MAT5gMZtPDP Herein, the carnot limit is derived without using the analogy working fluid "recycling" (Page 6). However, while the results they obtain seem rational, I find I find it difficult to follow their reasoning which is based on relations which are unfamiliar to me as an engineer. What I find particularly bewildering, the paper suggests that the difference in Fermi energy of the solar cell is dependent on the temperature of the radiation source (i.e., the sun in their example). As far as my understanding of semiconductor physics goes, the Fermi energy should be predominately determined by doping and in an theoretically ideal (and practically impossible) solar cell identical to the lower band gap edge for the p type and identical to the upper band gap edge for the n type - thus difference in Fermi energy is equal to band gap as long as current is infinitesimally small. If I read the paper correctly, it indicates that this is not the case. Does anyone have an explanation why this might be the case and if the reasoning done in the paper mentioned is sound? No, because the exergy output is always limited to the exergy input and in electrochemical cells, the input is not heat or heat related energy but chemical energy, which is mainly comprised of exergy Same reasoning as above, physical efficiency limit is 100% as energy input does not contain entropy and therefore output is not "obliged" to carry entropy

I'd tend to disagree with that argument. Gravitational energy is pure exergy, and thus is 100% convertible into work. On the contrary, radiation is just a type of heat transfer between the energy source (i.e., the sun or the 1000K object in my example). Consequently, photons have entropy and therefore their energy should not be fully convertible into work. I am not able to describe why I think that this must be the case in a more sophisticated way than the following but this argument seems convincing to me: If you're saying that the incoming photons have an exergy content of 100% (i.e., do not carry entropy), you are also saying that an imaginary system comprised of just an object at some temperature T and empty space will decrease in entropy over time as the object emits radiation and thereby cools down. While I am no expert on thermodynamics, I'd not subscribe to the notion that this is physically possible.

I absolutely understand that the cell I am describing is nonsense from an engineering point of view and impossible to make, but what I am interested in is if I could theoretically devise a cell that beats carnot efficiency - just from a physical perspective.

First of all, thank you for your replies! However, the underlying question if this ideal PV cell which I described could theoretically beat carnot efficiency is still not clear. If you're saying that efficiency reasoning for thermodynamic cycles do not apply to PV cells, that would mean that the carnot factor does not determine the theoretical upper limit of the ideal PV cell I described. If this is really true, wouldn't this mean that the device converts more energy into work than the exergy content of the incident irradiation is?

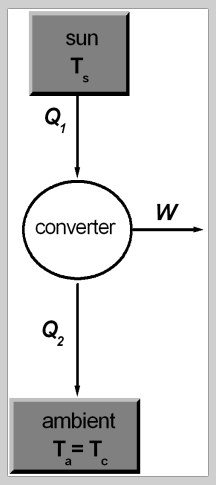
To be honest, I am uncertain if this setup could be described in terms of a working cycle, but I found literature (https://www.intechopen.com/chapters/47490) suggesting it. Generally, the notion that no device could beat carnot efficiency seems reasonable to me, so I accepted the depiction given in above citation: However, the "cycle" I came up with is a bit different: In my ideal PV cell, I don't see why the working fluid, which I assume to be the electrons, would emit heat after state 3 (Q2 in first picture). The heat emitted comes from the lattice I'd think, but I have to say that I am not a physicist so this is just a layman's guess. Nevertheless, the right hand side of the second image describes of how I imagined the "cycle" of the working fluid to be. Concerning temperature, why should it increase? Every incident photon "transfers" its energy to the outside electric circuit, so there is no heating going on inside the solar cell.

Assume you have a black body object at 1000K as a light source and an ideal* PV cell at 300K to capture that light. From a thermodynamic point of view, a maximum efficiency of 70% could be achieved (carnot limit), assuming both elements as black boxes. I am wondering how this figure manifests itself in the PV cell, and why the following reasoning is wrong: Think of an ideal theoretical PV cell, that has following characteristics: infinite amount of junctions stacked upon to capture 100% of the spectrum, infinite diffusion lengths of charge carriers, fill factor of 1 and no resistance in any electrical element. Given this cell, every incident photon would excite an electron from the VB to the CB in the semiconductor segment that has exactly the band gap energy of the photon. Consequently, every photon (and hence all incoming energy) could be utilized to power an external circuit -> 100% efficiency. While I am aware that it is impossible to build such a device, I'd expect to obtain the same theoretical efficiency limit via both a "black box" and a "white box" approach. Intuitively, I am not convinced by the second consideration. If this theoretical device would be put in front of the light source, it would cool down as itself emits Q~T_PV^4. I thus thought that the assumption of no recombination at all is even theoretically impossible and that some recombination must occur to release the heat required to sustain temperature. Can anyone give an intuitive explanation of what I am overlooking / getting wrong?

@exchemist Thank you very much for sharing your thoughts on this! It seems reasonable that the temperature of butane in the box will be always be slightly above -10, because if it would be exactly -10 °C, there wouldn't be net-vaporization except to account for diffusion losses and therefore no net cooling thus the temperature would increase. Good point. So, just to clarify, you're saying that because of the temperature of butane being slightly higher than -10° the diffusion of air into the box would be negligible because even though the flow of butane out of the box (which is driven only by a slight pressure gradient) is quite slow, the 'speed' of diffusion of air is even smaller?

@exchemist Thank's for your comment! That's probably true - scenario 1 is incorrect, as the flow rate of gas out of the hole will very likely be far greater than rate of diffusion. However, that does not apply to scenario 2 (real world example). When T_box is such that p_J_eq(T_box) = ~1bar , there won't be a pressure gradient driven flow of J and therefore diffusion of air into the box should happen, shouldn't it?

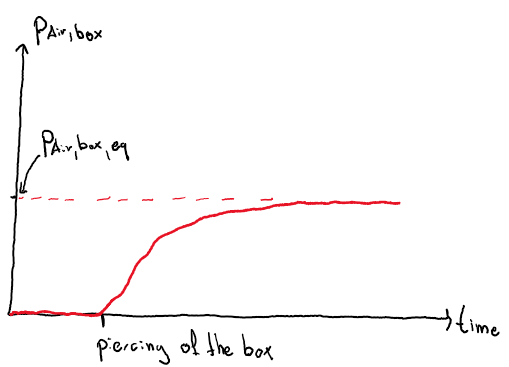
Dear community! I've recently been pondering about an intriguing thought experiment that can have serious consequences in the real world. Imagine you've got a box filled with a liquid J with a partial pressure p_J_eq(20°C) > 1 bar (higher than the air surrounding the box). If the box is closed, the remaining volume which is not occupied by J_liquid will be filled with J_gas at a pressure of p_J_eq(T_box,initial = 20°C). Now you pierce a small hole in the box, lets say 2mm x 2mm. According to common sense, gaseous J will escape and therefore more J_liquid will vaporize in order to increase p_J up to p_J_eq(T_box). Here, lets consider two scenarios: Scenario 1: Heat transfer from the surrounding air to the box and within the box is immediate (alpha & lambda = infinity), thus the temperature of the box and J within the box will not change (T_box=T_box,initial=20°C). Following that assumption, p_J_eq is not a function of time and will be constant at p_J_eq = p_J_eq(20°C) > 1bar. Here it gets interesting: Considering entropy and the fact that particles in ambient air move quite fast, it will be highly likely that at least some air particles will manage to get inside the box. My assumption is that the partial pressure of air particles inside the box p_Air,box will look something like the following graph. As far as I know, the equilibrium pressure of air molecules inside the box p_Air,box,eq should be equal to the air pressure surrounding the box (1 bar). My question here is, firstly, is this assumption right, and secondly, can anyone think of an easy way to estimate how long this will take? The only thing that comes to my mind is some CPU intensive particle modelling. Scenario 2 (real world): Heat transfer is not immediate, and the box will cool down until the partial pressure of J is approximately 1bar (the speed of which gaseous J particles escape is such that the rate of vaporization and the thereby induced cooling of the box is equal to the rate of heat transfer to the box). Therefore, p_J after some time will be p_J_eq(T_box,eq). Let's consider a real world example of where this might happen: Think of a gas cartridge filled with J=butane (p_Butane(20°C)=2bar, T(p_Butane=1bar)=-10°C (ball park numbers). Assume you unintentionally open the outlet of the cartridge without any safety mechanism so that the outlet is directly exposed to the surrounding air. In this case, butane will escape & air will get inside, and eventually the box will cool down to -10°C. According to previous reasoning the situation inside the box after some time will be following: p_Butane = 1bar, p_Air,box = 1bar. Now assume you close the cartridge again for later usage. First thing that comes to my mind is that the cartridge could theoretically burst as it heats up again as it is now filled with p_Butane(20°C) = 2 bar and some additional air with a pressure that is definitely above 1bar (it was 1bar at -10°C). Lets say it does not burst, and you use the cartridge again in a gas burner. Could this theoretically be dangerous? I reckon that the explosion limit of butane should not be an issue as the concentration of oxygen must be quite high. Whats your assessment of this?

You are absolutely right, thank you very much for your answer. This is the solution to my thought experiment. From my point of view a very astonishing reminder of how theoretical physics apply to such a simple practical experiment.

You just brought me to an idea, thank you for your input. Would it be correct to say that the increase in thermal energy inside the jar comes from the decrease of potential energy as the distance between magnet and solution decreases?

Thank you very much for your answers! Indeed such an experiment would be very interesting but unfortunately I do not have any lab equipment at home & university labs are currently closed. You are right, my example probably isn't very appropriate. But as joigus mentioned, just think of some magnetic soluble substance / macro structure. Putting a magnet near the isolated jar, the entropy in the jar will decrease by the entropy of mixing (or maybe a bit less as even with the magnet on one side there will still be a few molecules in the other parts of the jar). Now, as total entropy cannot decrease in closed systems (as the mentioned perfectly isolated jar is), there should be an increase in temperature and my question is, where does the energy for this come from as the system itself is closed?

Dear community! I've recently come across following intriguing thought experiment: Imagine a jar filled with water where infinitesimally small particles of iron dust are dissolved. The average particle diameter is small enough that they do not descend, therefore they are randomly distributed in the jar (high entropy). Now you take a magnet and hold it next to the jar - after some time has passed, the density of iron particles on the magnet side of the jar will be significantly higher than the density at the opposite side. Considering entropy, such a behavior should only be possible if the total amount of entropy increases or at least stays the same. However, this demixing/separation effect definitely has negative entropy, maybe not much but not zero. The only counteractive measure that would increase entropy I can think of is an increase in temperature. But if this is really the solution to this thought experiment, where would the energy necessary to heat up the system come from? Thanks a lot for every input

Dear studiot, thank you for your answer. I'll see what I can find. I've had look in my atkins as well, but they never mention that there are different conventions at all. I've found a copy of the book and this chapter tells very clearly what I was searching for. If anyone else who reads this is interested: Activity coefficients for molality are indeed no good tool to measure deviations from ideal behaviour. This is what Denbigh says:

Dear studiot, my calculation is meant to display the following exemplary scenario. I dissolve 0.5 mole of J in one liter of water. Therefore, I've got: 0.5 moles of J 1000g/18 g/mole = 55 moles of H2O Further, as you pointed out, I assume that the volume does not change. Thus, I can calculate the mole fraction x_J and the molarity of J. This in turn shows that the activity coefficients y_x and y_c are different, what leads to the confusions I pointed out above.

Dear community! I've just found a few contradictions in a topic I've never put much thought in. In order to calculate the thermodynamic activity, different formulas are being used. According to Wikipedia and common sense, these formulas should return the same value: According to IUPAC, the standard values for concentration and molality are 1 mole/l and 1 mole/kg respectively. Thus, this relation is only possible if the activity coefficients for x,b,c and so on are different. Consider a simple example, 0.5 mole of a substance J dissolved in 1 l of water (~55 mole): As you can see, the values of the activity coefficients depend on which formula I use. This leads to a few confusions: Often, the activity coefficient is interpreted in a quantitative way, for example, what a activity coefficient greater than 1 means. However, when I look at my calculations, there is no point in interpreting y as its value is quite random and depends on the equation I am using. When calculating the activity coefficient, for example with the Debye-Hückel equation, just looking at the equation, how do I know which y (y_x,y_c,y_b) it returns?