John2020

Maybe I am wrong on this thread but certainly not on the other with the translation screw. I still cannot see it. Do you see any contact force pushing the mass m_T (is there any bare hands pushing and I am so blind I cannot see them?)

OK. Thread is closed!

These are contact forces between the belt and the drive wheel not upon the surface of mass m_T. The moderators are probably sleeping. Hey, wake up! You have to close this thread!

I stated that mass m_T is one with the belt (rubber). I used the word "glued" to point that the belt and the mass m_T is one indistinguishable (melted belt together with mass m_T). Contact force means for me, something that will effectively push mass m_T (like pushing with bear hands a car. The hands contact the surface of the car in this case). Here as also in the mass m:T on the translation screw there is no push (no contact with something that pushes it). Therefore, in both cases we have a pure inertial force (a pure varying momentum of mass m_T). It is a conversion of angular momentum to linear without having a contact force.

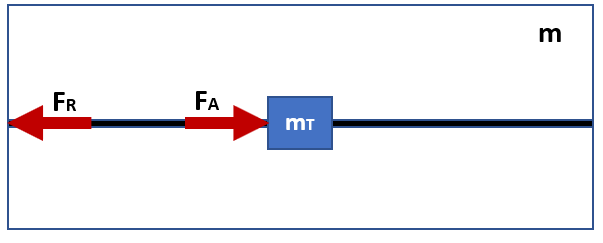
What I am trying to say is that on m_T applies no contact force. Only in Fig.2 we have contact forces the action-reaction pair FA and FR. It is the same topic. If you insist that we have in both threads a contact force on m_T then I ask from the moderator to close this thread too. It is a waste of time for you and for me.

But effectively there is no contact force, otherwise I would have drawn it. One cannot apply a contact force to apply the laws of physics from the moment there is none. It is just a changing momentum of m_T. Isn't this correct? Assuming there is no dissipation of energy due to friction, the changing angular momentum of the gear is converted to linear acceleration on m_T without applying a contact force. Isn't that right? Furthemore, let us say mass m_T accelerates with 1 m/sec^2 to the right as seen in Fig.1. Is there a counter acceleration on the rest of the isolated system? Let us switch to the old thread that was recently closed for a moment. Does your statement above applies for the mass m_T (blue component) on the construction of the linear actuator?

In Fig.1 it appears the mass m_T to accelerate without a contact force. How the free body diagram assumes one from the moment there is none (just a varying momentum)?

We have to ignore tensions and stuff, just the action reaction principle I would like to involve. For me there remains still an issue: Mass m_T is accelerating without applying a contact force. Is this correct?

Where exactly those internal forces will appear?

I think it was a bad idea this thread. Assuming the mass of the belt is negligible compare to m_T could we continue? IF not then close the thread.

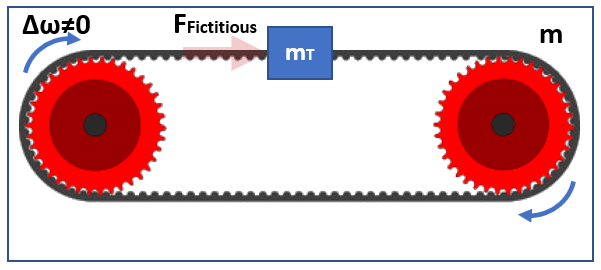
I make another attempt to make all these clear:: 1.The boundaries of the system is the blue frame in Fig.1 2.Regarding the mass m_T when I sat coupled I mean it is one thing with the belt underneath (like being glued). I will make a little bit later a new design in order to have everything in place (along with the couple that turns the gear). Belt and mass m_T is one thing that way I present it, as one thing. It is like during the production of the belt we have melt belt material equal to mass m_T together with the belt part at that location.

Then it does not accelerate the blue box. Ill try a different way of answering: If the force Ffictitious in Fig1 acts on the blue box then the force Ffictitious is not fictitious; the answer to a) is "no". I didn't expect the drawing of an unreal force to be a problem. Anyway, the faded arrow is not a real force, it does not exist. Remove the label Fictitious and the faded arrow. I hope now it is clear. Forget (a) and (b) and focus on the following question: While mass m_T is being accelerated, do emerge or appear any kind of reaction forces that may affect the rest of the system (isolated)?

1.The faded arrow is not a real force (I already mentioned this) 2.The m_T is coupled on the belt 3.The belt is being accelerated (see Δω≠0) 4.Due to (2) and (3) the mass m_T accelerates 5.Due to (4) the acceleration of mass m_T appears as being influenced by a Fictitious Force (Inertial) Obviously, it was made clear we found the answer on (a). So, what about (b)? Do you see any kind of reaction force to emerge/appear while mass m_T is being accelerated?

I think you are making a mistake here. A linear accelerating or rotating reference frame implies a non-inertial frame of reference that further implies the shown force should be a Fictitious (Inertial) Force or not?

There are no hidden parts. Mass m_T moves just because of the accelerating belt (mass is coupled on the belt). The faded arrow indicates a non-real force.

I mean to find an answer on the two questions a,b I mentioned on my first post.

I didn't draw it actually. It is a hidden couple (back side) that creates a varying torque that leads to a varying angular velocity. I have to go to sleep. I will be very happy if you can help me find an answer on those two questions. See you tomorrow.

I think you didn't notice that I explicitly wrote the change in angular velocity Δω is not zero that implies a varying momentum on mass m_T (Fig.1). In case Δω = 0 then the mass m_T would have constant speed.

I think this is what I did or not? Could you help me answer the questions above?

Of course not. A better name is "Inertial".

Fig.1.Isolated System and Internal Fictitious Force \[\Delta \omega \neq 0 \Rightarrow \sum{F}_\mathrm{int} = {F}_\mathrm{Fictitious} \neq const. (varying) \] \[\sum{F}_\mathrm{int} = \frac{m_\mathrm{T} \cdot ({u}^{\prime}_{\mathrm{cm}}- {u}_\mathrm{{cm}})}{\Delta t} \neq 0 \] \[\frac{\Delta {p}}{\Delta t} = \frac{m \cdot ({u}^{\prime} - {u})}{\Delta t} = \frac{m_\mathrm{T} \cdot ({u}^{\prime}_{\mathrm{cm}}- {u}_\mathrm{{cm}})}{\Delta t} \] \[{u}^{\prime} \neq {u} \Rightarrow {u}^{\prime}_{\mathrm{cm}} \neq {u}_{\mathrm{cm}} \Rightarrow {a} \neq 0.\] Fig.2.Isolated System and Internal Collinear forces (Action-Reaction pair) \[\sum{F}_\mathrm{int} = \left( {F}_\mathrm{A} + {F}_\mathrm{R} \right) = 0 \text{ (collinear)}\] \[\frac{\Delta {p}}{\Delta t} = \sum{F}_\mathrm{int} = \frac{m \cdot ({u}^{\prime} - {u})}{\Delta t} = 0 \] \[\frac{m \cdot ({u}^{\prime} - {u})}{\Delta t} = \frac{m_\mathrm{T} \cdot ({u}^{\prime}_{\mathrm{cm}}- {u}_\mathrm{{cm}})}{\Delta t}\] \[{u}^{\prime} = {u} \Rightarrow {u}^{\prime}_{\mathrm{cm}} = {u}_{\mathrm{cm}} \Rightarrow {a} = 0.\] Could someone help me on these questions: a) In Fig.1. is what is shown a Fictitious force? b) IF (a) is true, is there any reaction force being exerted on rest of system?

No external forces apply on the system. I meant you treat the problem like being a classical one with null external forces by ignoring what happens inside. That was all. Take your time I am also busy. See you in the afternoon! I will try to use the Langrangean you provided to find a solution to the problem, later in the evening. Be well!

a) This assertion has to be demonstrated mathematically. b) You treat the problem as Newton did, meaning assuming just null external forces. c) If Langrangean cannot by design consider the inner parts of the system then it is not the right tool for this problem. d) The fictious force that acts on m_T as being reactionless has to be taken into consideration. Could you write down the momentum conservation for the above system without using Langrangean? I forgot something. I am sorry, too.

Use the simplest possible description. e.g 1 degree of freedom, angular velocity ω , mass m_T, mass m, linear velocity u_T (for m_T) and linear velocity u (for m). Yes the construction is an isolated conveyor belt system.

1) Gears have a constant angular velocity. (a) Would the CoM change? (b) Would the isolated system (m) start to accelerate? 2) Gears have an increasing (non-constant) angular velocity. (a) Would the CoM change? (b) Would the isolated system (m) start to accelerate? Could someone develop simple classical mechanics equations or even Lagrange formulations to answer the above questions?