Hi everybody!
First of all I have to make clear that I am not a physicist, however as many other science fiction enthusiasts, I have an interest in alternative propulsion methods (reactionless drive etc). My theory is published in a non-arxiv.org repository and essentially explores the feasibility of constructing a reactionless drive (an initial mechanical prototype). As we know Newton's 3rd law forbids the construction of a device that may move by means of internal forces, something that all propellantless propulsion/reactionless drive theories tend to ignore. The conclusion of my research can be briefly stated as follow: A reactionless drive may become feasible if and only if Newton's 3rd law is not the whole story that means it may probably be incomplete.
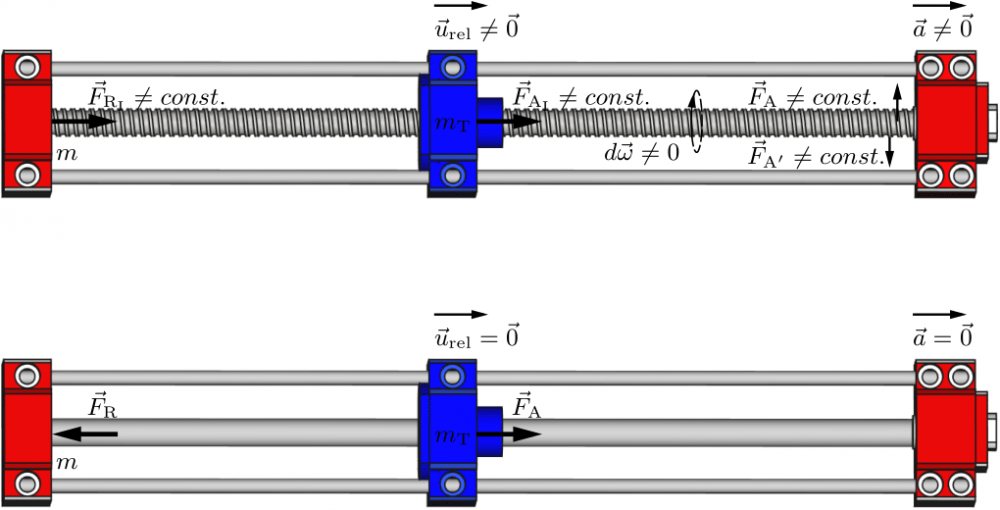
Fig.1 - Proof of concept. Action--reaction forces in isolated systems. Upper: Induced internal forces. Redeployment of the center of mass and acceleration of the system. Lower: Collinear internal forces. No change in the center of mass and no acceleration of the system.
Attention! The induced internal reaction force was not deliberately inverted (same direction with the induced internal action force) but as a consequence of the mathematical proof.
The mathematical description assumes the reactionless drive (see Fig.1.Upper) is internally powered (motor and power supply on board (appears hidden in Fig.1 - Upper)) as also there is no dissipation of energy due to friction (ideal machine). Starting from the conservation of angular momentum, the net external and internal torques in FIG.1 - Upper, are
\[\sum \vec{\tau}_{ext} = \vec{0} \]
\[\overbrace{\vec{F}_{A}}^{\longrightarrow} + \overbrace{\vec{F}_{R}}^{\longleftarrow} = \vec{0} \]
\[\vec{r}_{A} \neq \vec{r}_{R} \Rightarrow \vec{\tau}_{A} \neq \vec{0} \text{ and } \vec{\tau}_{R} \neq \vec{0} \]
\[\sum \vec{\tau}_{int} + \vec{\tau}_{A} + \vec{\tau}_{R} =\vec{0} \]
\[\sum \vec{\tau}_{int} + \left(\vec{r}_{A} \times \vec{F}_{A} \right) + \left(\vec{r}_{R} \times \vec{F}_{R} \right) = \vec{0} \]
\[\sum \vec{\tau}_{int} + \left(\vec{r}_{A} \times \vec{F}_{A} \right) + \left(\vec{r}_{R} \times \left(-\vec{F}_{A} \right)\right) = \vec{0} \]
\[\overbrace{\sum \vec{\tau}_{int}}^{\curvearrowleft} + \overbrace{\left(\left(\vec{r}_{A} - \vec{r}_{R} \right) \times \vec{F}_{A} \right)}^{\curvearrowright} = \vec{0} \]
An ideal translation mechanism (translation screw in FIG.1 - Upper) can maintain, amplify or reduce the magnitude of the input force by delivering the same amount of energy (no energy dissipation through friction) entering the system (energy conservation). At this point, developing a general expression for the net induced force requires the introduction of the dimensionless factor \(n_{T}\) (ideal mechanical advantage) along with a definition of the net induced torque. Hence,
\[n_{T} = \frac{|\vec{\omega} \times \left(\vec{r}_{A} - \vec{r}_{R}\right)|}{|\vec{u}_{T}|} = \frac{\left(2 \pi |\vec{r}_{A} - \vec{r}_{R}|\right)}{|\vec{l}_{T}|} \]
\[\overbrace{n_{T} \sum \vec{\tau}_{int}}^{\curvearrowleft} + \overbrace{n_{T} \left(\left(\vec{r}_{A} - \vec{r}_{R} \right) \times \vec{F}_{A} \right)}^{\curvearrowright} = \vec{0}\]
\[\sum \vec{\tau}_{T} = n_{T} \sum \vec{\tau}_{int}\]
\[\overbrace{\sum \vec{\tau}_{T}}^{\curvearrowleft} + \overbrace{n_{T}\left(\left(\vec{r}_{A} - \vec{r}_{R} \right) \times \vec{F}_{A} \right)}^{\curvearrowright} = \vec{0}\]
Dividing the above by the position-vector magnitude \(|\vec{r}_\mathrm{A} - \vec{r}_\mathrm{R}|\) yields
\[\overbrace{\frac{\sum \vec{\tau}_{T}}{|\left(\vec{r}_{A} - \vec{r}_{R} \right)|}}^{\longleftarrow} +
\overbrace{\frac{n_{T} \left(\left(\vec{r}_{A} - \vec{r}_{R} \right) \times \vec{F}_{A} \right)}{|\left(\vec{r}_{A} - \vec{r}_{R} \right)|}}^{\longrightarrow} = \vec{0} \]
\[\sum \vec{F}_{T} = \frac{\sum \vec{\tau}_{T}}{|\left(\vec{r}_{A} - \vec{r}_{R} \right)|}\]
Due to conservation of energy, in an ideal machine (FIG.1- Upper), the power output equals to the power input:
\[P_{T} = P_{A} \Rightarrow
\frac{|\sum \vec{F}_{T}|}{|\vec{F}_{A}|} = \frac{|\vec{\omega} \times \left(\vec{r}_{A} - \vec{r}_{R}\right)|}{|\vec{u}_{T}|} = n_{T} \]
The above shows when the \(\vec{F}_\mathrm{A}\) is constant then, the angular velocity of the translation screw \(\vec{\omega}\), the induced force \(\vec{F}_{T}\) and the translational velocity \(\vec{u}_{T}\) of mass \(m_{T}\) are also constant.
The force \(\vec{F}_T \) can be also written as
\[\sum \vec{F}_{T} = - \frac{n_{T} \left(\left(\vec{r}_{A} \times \vec{F}_{A} \right) + \left(\vec{r}_{R} \times \vec{F}_{R} \right) \right)}{|\left(\vec{r}_{A} - \vec{r}_{R} \right)|} \]
\[\sum \vec{F}_{T} = - n_{T} \left(\vec{F}_{A_T} + \vec{F}_{R_T} \right) = \text{const.}\]
Nevertheless, the above equations address just the motion of mass \(m_{T}\). By expanding the ideal mechanical advantage to include varying angular and translational velocities, a new net force expression is derived that may apply for the motion of the system as a whole. Thus,
\[d \vec{\omega}\begin{cases}
= \vec{0} &:\quad \vec{F}_{A} = \text{const.} \text{ and } \vec{F}_{R} = \text{const.} \\
\neq \vec{0} &:\quad \vec{F}_{A} \neq \text{const.} \text{ and } \vec{F}_{R} \neq \text{const.}
\end{cases} \\
n_{r} = \frac{|\mathrm{d} {\omega} \times \left(\vec{r}_{A} - \vec{r}_{R}\right)|}{|\mathrm{d} \vec{u}_{T}|}, \\
\sum \vec{F}_{ind} = - \frac{n_{r} \left(\left(\vec{r}_{A} \times \vec{F}_{A} \right) + \left(\vec{r}_{R} \times \vec{F}_{R} \right) \right)}{|\left(\vec{r}_{A} - \vec{r}_{R} \right)|}, \\
\sum \vec{F}_{ind} \propto d \vec{\omega}, \\
\sum \vec{F}_{ind} = - n_r \left(\vec{F}_{A_I} + \vec{F}_{R_I} \right),\\
d \vec{\omega}
\begin{cases}
= \vec{0} \Rightarrow \vec{d} \vec{u}_{T} = \vec{0} &:\quad - n_{r} \left( \vec{F}_{A_I} + \vec{F}_{{R_I}} \right) =\vec{0}, \\
\neq \vec{0} \Rightarrow \vec{d} \vec{u}_{T} \neq \vec{0} &:\quad - n_{r} \left( \vec{F}_{A_I} + \vec{F}_{{R_I}} \right) \neq \vec{0}.
\end{cases}\]
Applying the mass transfer mechanism (FIG.1 - Upper), yields
\[\mathrm{d} \vec{\omega} \neq \vec{0} \Rightarrow {d} \vec{u}_{T} = \vec{u}_{rel} \neq \vec{0}, \\
\frac{\mathrm{d} \vec{p}}{\mathrm{d}t} = \sum \vec{F}_{ind} = - n_{r}\left(\vec{F}_{A_I} + \vec{F}_{R_I} \right) \neq \vec{0},\\
\frac{\mathrm{d} \vec{p}}{\mathrm{d}t} = -n_{r} \vec{u}_{rel} \frac{\mathrm{d} m}{\mathrm{d}t} \neq \vec{0} \Rightarrow \vec{a} \neq \vec{0}, \\ \]
I will be very happy if you can help me evaluate the above idea!