John2020

OK!

Clear. I just addressed above the case with the rotating frame. Of course in the non-rotating frame we have no centripetal force.

For constant angular velocity there is an equilibrium in your example where the centripetal equals to the centrifugal force. The same conditions apply for my example when the angular velocity is constant. Forget about the previous examples, I made some errors there. Let us focus on the example with the rotating mass. Is the drawing clear for you? Do you have any questions?

In your example the system is in equilibrium , thus no acceleration and no centrifugal force is being developed on the rotating frame (assuming the ball is not thrown). That is all OK. My example is different since the system is not in equilibrium because of the change in angular velocity. Consequently, in my example there is an inertial centrifugal at play. Is it clear for you? All clear. We may proceed now.

I think you misinterpret the drawing. Initially the ball is at r1 when the rotor turns with constant angular velocity. r does not increases by its own. We have a fixed length of a rigid rod where mass m is allowed to slide over it but it is held in r1 position due to friction (static friction should be better to say). On increasing the angular velocity of the rotor, the inertial centrifugal force has to overcome the static friction and push mass m (acceleration) upto position r2. Up until the r2 point the angular velocity increases thus the centrifugal too. Assuming being accelerated all the way down to r2.

The rotor turns counterclockwise (red arrow) and the stator clockwise (blue arrow). It is not so clear to me. Anyway, proceed further by analyzing my example to see if it fits to the above description. I have to go and I will be back a little bit later.

I think this is already shown on the drawing (see the red and blue direction vectors).

Yes.

In my example it is clear there is centrifugal force at play in the rotating frame of reference.

Your assertion does not represent the situation above. Maybe I was not clear (I thought it was obvious). In order the mass m to go to r2, presupposes an increase in angular velocity ω2 that implies a centrifugal force will rise pushing mass m to r2 point. This is how I present the situation with the drawing. I cannot follow you. The rotor is powered internally being the system in outer space. We start the rotor until it acquires a constant angular velocity and then we leave it. After some secs, there is an internal mechanism that will increase its angular velocity. Moreover, the rod is rigid that means the angular momentum can be transferred to mass m.

It is not clear to me, however not so important for the analysis. Does the rectangular frame has an opposite direction with that of the rotating circle? If yes then, OK. It is like the drawing depicts a situation while being on the circle rotating counterclockwise, the surrounding space turns clockwise. If this is the case then, I agree, otherwise it doesn't make sense to me. However this would negligibly affect the analysis (just the direction the ball follows in your example).

Yes, we can move on to the analysis. The right frame rotates clockwise. Seeing the rotation of the circle on the left, shouldn't the right frame rotate counterclockwise in order to agree with the rotation of the circle on the left?

Very nice animation that demonstrates the difference between the non-rotating and the rotating frame of reference! I agree (analysis for my example).

Could you make the analysis on the last drawing with the rotating mass and to answer on (a) and (b)? Please present an analysis as also give your answer for (a) and (b).

I think that would lead to wrong conclusions. For e.g. analyzing the rotating mass in outer space (see the drawing I shared a couple of posts above) from an inertial frame of reference, will the motion of the ball (m) be attributed to a real force (and not to inertial centrifugal) that implies a reaction force (upon the rest of the system) appears at the same moment? I have to go to sleep. See you tomorrow.

So, when I need to make an analysis of a rotating object, I have to place the frame of reference rotating along with the rotating object, right? After finding what is going on there, I switch to the inertial reference (my PC screen) and check how the finding in the rotating object may affect the observation from the inertial frame of reference (my PC screen). I think the @The victorious truther mentioned something similar.

You mean it should have a mass attached on its surface, at least in order the fictitious forces to manifest?

Frame of reference: I am sitting in front of my PC screen (I don't know how you interpret this), seeing the picture of this rotating mass device (Prediction: accelerating in one direction). Prediction: Mass (m) will accelerate due to the inertial centrifugal force (no reaction will appear at the rest of the system), creating an accelerating change in CoM that will eventually accelerate the system (M+m) as a whole. Could someone please do the math for whatever prediction? I am just curious how will this problem be handled.

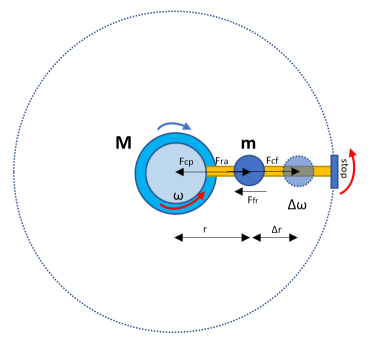
I have done several mistakes describing the situation with the Fig.1-Upper. I should have mentioned while the bolt turns with constant angular velocity the frame of the construction rotates in the opposite direction by simultaneously displacing the mass m_T to the right. Under such conditions, the analysis makes sense to be done as seen from the rotating frame of the construction. Being in the rotating frame of the construction, I was expecting the acceleration of the screw (increasing angular velocity) to induce (over the translation screw) an Euler like force (more accurately an artificially conducted by the translation screw mechanism) that will accelerate the mass m_T to the right. Consequently, since this force wouldn't be created by a real force (like pushing by contact, again according to my expectation), the acceleration of mass m_T would result in the redeployment of the CoM without being able to transfer mass in the opposite direction due to the construction topology, thus the system would accelerate as a whole. This was the initial idea behind the construction in Fig.1-Upper. Regarding inertial and non-inertial frame of reference, I have to admit is very confusing for me, as also irrelevant (a rotating object will induce those fictitious forces that has to induce and a non-rotating one, will have just plain Newtonian acceleration (if any)). If the construction could work then, the change in the rotational energy (accelerating screw) would be converted to a change in the kinetic energy of the mass m_T and eventually to the whole system. This transition would force the construction frame to stop rotating (resulting in a non-conservation of angular momentum due to the conversion of rotational to kinetic energy). Again this is my view, which is probably wrong as all the above. Rotating mass m in outer space. M: mass of the rotor m: mass that may move radially ω: angular velocity yellow rod: rigid rod Fcp: centripetal force Fra: reaction force Ffr: friction force Fcf: inertial centrifugal force while Δω ≠ 0 The rotor provides a constant angular velocity while the mass is at distance (r). When the angular velocity increases by Δω within 0.1 radians: a) How mass (m) will be affected from the change in angular velocity? b) How the system (M + m) will be affected from the change in angular velocity? Note: Some years ago, I conducted a very simple experiment with a sample of Pb (lead) metal being suspended by a thread hooked under a weight balance (0.001 grams resolution) and applied a DC magnetic field of Nd Magnet that showed something interesting (video available) that depicts the above situation (according to my view).

I am preparing a drawing to explain all these and we will make the analysis for three cases: rigid rope, semi-rigid and non-rigid rope.

Just assume for a moment it is possible without releasing the energy over a photon. The nucleus and the electron absorb this energy by converting to radial momentum. I mentioned above we have a rope that is non rigid radially that means the tangential velocity may also change. Thus, at that moment as Ghideon also noted, the Centrifugal will be larger than the centripetal resulting in small mass displacement radially.

Let others answer this if they like. In the meantime when you have a motor suspended by a thread and start it and let us say starts and stop aftet 1/4 of rotor complete cycle what would the motor do?

Your analysis is simply wrong and contrary to observation.

Correct. Next time take the hammer you mentioned and try those steps I proposed and tell what you experience.

So, what do you predict to happen after all these? The small mass will move for a short time radially and at the same moment what is expected for the man if being in outer space?