CuriosOne

Yes, but I use 3d to create 3d video games, 3d models, basically 3d "toys" and when I render the images it looks very similar to images I see in the real world.. The same is true for animations that uses the evolution of time to move. For instance, how do numbers "know" left, right, up or down?? If you say computer software programs them, then that's more than obvious, but say we do math on plain "paper" and pencil, how then can the numbers do what they do in 3d space x,y,z?? I guess I'm asking what links "instructions to numbers in the phyiscal world without computers?? The universe has been here for billions of years before the thought of the computer processor..

Do you think that " triangulation" has something to do with the "ELECTRON CONFIGURATION" and color charge?? Afterall, pixels are made of 3 colors RGB and the "outer regions" of "objects" either obsorb or emit electromagnetic radiation. But then, how do triangles, pythagoreon therom and electron configuration relate?? After all, we use the same visual perception using the Pythagorean Theorem. Seems like everything uses 2 points in space shared by an origin in Cartessian Space..

I've been using Maya for the past 10 years, I love 3d...

Still sort of confusing becuase all I see are 6 sides of 1 dimension ( 1 flat hyper plane of 6) and rotations look reflected on all 6 dimensions of the box. Its mind boggling...Atleast its how I perceive it to be.

I created my 1st ever computer program 20 years ago in C++ for video games until i found an easier and faster method with Python, but C++ is very time consuming..It is however industry standard and professionally efficient I must say.. About our distances and 2 points, is zooming in a subdivision process of triangulation? I keep thinking about the rendering engine itself, the smoother a mesh the more render time...((IE more triangles = more processing power..)) Quads to Triangles final process. I've always wondered why that was... Just want to add a point is dimensionless right? I'm a CGI artist as well, very knowledgable in this field.. "One Very Important Question" What units do theses points of the extremely small use??? The points that The Pythagorean Theorem predict between a triangle to its hypotenuse?? And are theses in 3 since a triangle has 3 points..

Never knew The Pythagorean Theorem had multi puposes use, especially the sequencing and summing up the very short straight lines part, or zooming into to them.. Can I see an example of this please? Reason I ask is becuase It clarifies my knowledge on calculus since it uses it too..

Very insightful thXxxx... The definition of zero being a number now answers most of the point of calculus, "But" in regards to arbitrary small differences not being numbers, what are they?? functions?? I read?? My focus then would be on the operators on simple functions that output other functions not numbers as converged "things" whatever they connect to at this point. From what I'm understanding it sounds like a terrasac hypercube with infinite limits of functions within functions of operators...Is this right? If "things" are converged I can see why this would be the case in regards to a refference atlas like cartessian space and the "points" on it in 3d, hieght, width and depth.. Is this the way to think about it? The Greek lower case delta δ has my attention now. This Makes Sense ThnXxxx The second one is important to us because it is not only about small differences in the values of the variable that follows it, it is about arbitrarily small differences. This means that δx is not exact but may be made smaller and smaller indefinitely. So it is not a number it is a sort of function. Also since it is not a number it can never be zero, since zero is a number. This brings us neatly to the idea of limits.

This is getting very intresting now... I'm glad I posted this OP bold question, this information is inspiring thnXxxxx.

Will definetly try this out, looks fun thnXxxxx...I will try too slow down too, I agree with you...

If getting closer "Where is x at then?" At the edge of space??? And how do we know how far to zoom in and out, x is not a camera lense..😎

KE = (1/2) mv^2 looks correct...

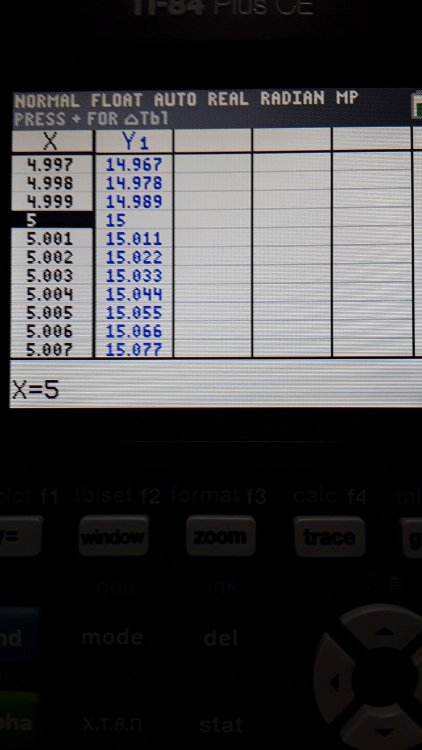
"I do get what your saying" But its said Newton used the pyramids to create calculus...Is this true?? The extent of pi and the pythagorean theorem used in calculus "right angle" triangles leads one to think the pyramid contribution may be true... Even E=mc^2 looks very familiar to F=mv^2.... This explanation is very helpfull, thnXxx and your right about x=0 If x=5 but you can't reach zero, is there a sequence of numbers going on, such as a list for x and y values?? I assume that's what they are..Maybe you can show that list, as I just place it in my calculator and press generate list this is what I got...

I'm seeing many calculus problems that use the ideas of right angle triangles, but seldom do I come across the use of our Pythagorean Theorem spot light to the rescue in them. Infact I see much confusing or complex "hard to understand" functions and or equations, that never tell you, "You need the Pythagorean Theorem" to solve this problem. Maybe a technique to keep readers flipping pages whom knows.. In regards to rates again we have it here, a calculus problem... Please note: I'm seeing most of the time that there appears to be 2 things in motion at the same time in calculus problems, 2 changing lenths or distances but "one" time component "in the general sense." ds/dt anyone??

Understood, and thnXxx. Now if u may please, for the time dimension (t) is this the fourh dimension? If so does it work the same as with the 3rd dimension ie x y z translations? Do we even use the fourth dimension for any purpose other than time?

Which dimension goes up and down? Say as we perceive falling objects from a building down to the ground with the force of gravity of coarse acting on it bouncing up then repeating till it stops.

Sounds very intresting...."in regards to tossing a dart on a board bull's eye with both in circular motion"... Where could I see a formula for this if you may?

Understood, but earth and the asteroid are in motion right? There is a reason I ask. Sounds like this only works for close range proximity? I assume.. Sounds like calculus..😎

This is more clearer and thanks.. I'm trying to tie this concept in with the pythagorean theorem since it does use some concept of geometry.. Much like music in mono and stereo, there is a big difference, but it still is what it is....Hymmm maybe being an advance human has its advantages who knows..

3rd dimension equivalent to height ,depth and thickness, what about 'scaling' making something bigger or smaller? Can I see an example of the rocket reaching an asteroid, and the time example to hit the asteroid please..

So the 3rd dimension is an illusion?

What is the 3rd dimension and how do we visualize it?

Why do we need to imagine it as I thought our concept of geometry was 3 dimensional.. And I need to add this question: Is Time One Dimensional?

Thnks for the link...I do hope however I can have some answers to my question about limits earlier....in regards to: Lim x->0 = x^2 -25/ x-5 BEFORE" we add numbers let's speak reason "please." does x^2 -25 represent y the numerical value, the value that does not change? and does x-5 represent the changing variable x? Where do these changes in position take place??? Do they take place on the orbital paths themselves, since "force" causes the planets to move?? Looks like orbital paths are "discountious" to me, hence the Title of my post. So Calculus is a tool for orbits and nothing else??

I've read number theory could be the more suitable approach as to use the number theory finds and apply them or plug them into our f(x) function limit issues. After all, there has to be many variations that define the same value as there is many ways to play the drums to a melody....I guess it depends on reliability, trust and efficiency at this point if the world depended on such a system. Yes, differential calculus focuses on rates of changes and the ""Pythagorean Therom"" is extensively used with it. The notation that expresses these functions also change which gets very frustrating, here is an example: dy/dx or df/dx or df(x)/dx or D, xy or d/dx or f'(x) or y' and etc etc "All Mean The Same Thing." Ive been observing this for years now of which had me confused for about 4 years until I caught onto it.. let me show a number example of these limits finally "I found one" and we can dissect this from here as a visual guide for direction, becuase the functions are confusing me and maybe others.. Lim x->0 = x^2 -25/ x-5 as "delta" x approaches 0 "BEFORE" we add numbers let's speak reason "please." does x^2 -25 represent y the numerical value, the value that does not change? does x-5 represent the value that does change?

Let's say the interest is 2 stationary vibrating "particles" in space (a,b )and we want to know how the "vibrations" of both interact within a certain "limit "before" change...Or even better, we want to know "which vibration is a or b, since they are all mixed in with each other...If that's even possible if this were a case involving trillions of stationary particles vibrating in space..