Cosmic Yoyo

(apologies, my edit is talking about reduced spheres and the proof for spheres)

Hi swanson First of all, I decided to go algebraic half way through but forgot to replace the angle dimension. Second, in my explanation, for the sake of brevity, I didn't mention the inverse square relationship with respect to force in the beam example. This is a second factor that enhances the overall effect. I have identified this in other documentation, but like I say, brevity. Now to the maths - here's the formula to find the force acting on the hypotenuse: https://en.wikipedia.org/wiki/Newton's_law_of_universal_gravitation The force on the individual weights is F = G x (m1 x m2) / r2. Now it's a case of substituting the F calculated above into the triangle to resolve the vertical and horizontal components. All this requires is using F.cosø and F.sinø as specified in the cited reference, then multiply by two for both sides. I'm not quantifying the height and separation, but the two comprise the horizontal and vertical components of r - distance to the centre of the Earth. Going back to my example, let's say the angle is 45º, elevation at the beam centre is 6500Km, separation is 13,000 Km. For those playing at home, I'd like to emphasise using 45º because it makes going between front, angled and top views easier because 2D to 3D is a case of multiplying by 1/(sqrt)2 or 0.7071 both ways. So for the centred weights, using constants from here: https://en.wikipedia.org/wiki/Gravitational_constant F = (G x mass of earth plus 2Kg) / r^2 We take G x mass of Earth as a constant of 3.986 x 1014, this is the GM in the vis viva formula. => F = 3.986 x 1014 / 422,250,000 (Km, but the formula uses metres so add 6 zeros, exponent value is 4.225 x 1013) => F = 9.43 N/Kg Divide by 9.81 to convert from N to Kg, multiply by 2 because there's 2 force triangles mirrored. So with these values, the left hand scale reads 1.92 Kg. Now for the separated values: Radius is 6500Km x (sqrt)2 = 9192 Km, so r2 = 84,500,000 (Km) F = 3.986 x 10^14 / 8.45 x 10^13 => F = 4.7 N/Kg Now is where we do the divide by root 2 to fond both the horizontal and vertical components *Note - to repeat, I didn't include this first step again for the sake of brevity, a much smaller beam would have a much less pronounced variation in gravitational strength and I didn't want to complicate communicating how the force diagram works usually. The significant difference going on here is the r2. My experience with this comes from truss analysis where the active forces aren't subject to modification in this way. F (vertical and horizontal) = 3.34 N/Kg So with these values the right hand scale reads 0.68 Kg. Edit - I hope whoever proved centre of attraction = centre of mass took this into account. I don't know, this isn't my sandbox.

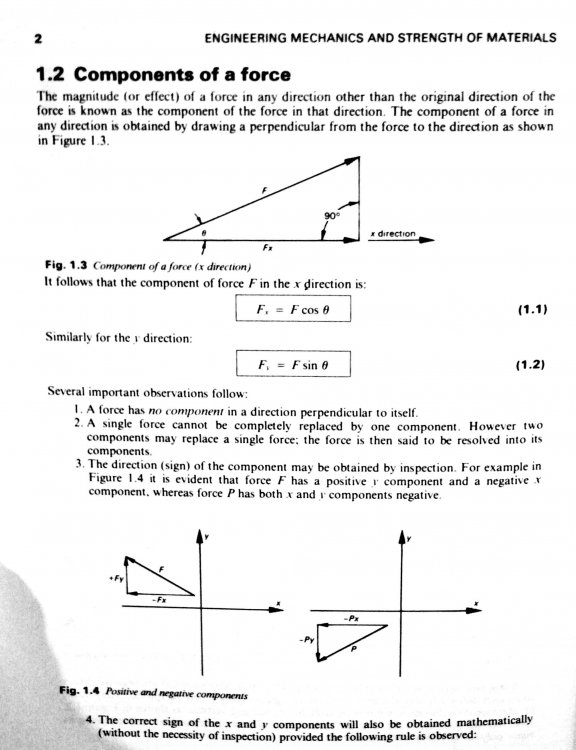
swansont "No work is done in elevating mass? Really? You think that comes from assuming the force is parallel? The work done in elevating a mass is its potential energy." This is baked in to any formula treating a distributed mass with significant variation in field direction as a point like object in the location of the centre of mass. If both sides are elevated by moving in opposite directions, it certainly does requires work, but when the sides are treated as a point like mass with a single location, the elevation in this direction doesn't register as a change in elevation for the centre of mass. Here's a diagram, would you like me to solve for the ?

swansont This is the following sentence for the quote in your third question. I identify the presumption in what you quoted and identify it's not precise in the next sentence. " This is an estimation, based on the application of the definition of weight." This could be expressed more specifically, for orbiting bodies, mass usually isn't a concern and the flawed definition is derived and shared with the flawed definition of weight because it involves using the centre of mass for all calculations. I would be looking worse if I said the centre of mass is wrong. Instead, I'm focusing on apparent weight, because the distribution of mass *is* important and makes a difference. Once you depart from ignoring mass as one can when examining small structures, turn your head and apparent weight is the principle you need. My recommendation is to split the structure in the middle and calculate for the two resultant centres of mass. (The next step involves separating out the middle due to drift - so you have three centres of mass). When calculating orbits, we don't worry about the slight variance in the direction of the gravitational field. It hasn't been important, because the arc angle (edit - of space craft) is tiny. I have attached how the forces are calculated between two points, this is literally the second topic after signing conventions in my structural engineering book. The important thing is that apparent weight and calculating orbital trajectories use the centre of mass for the calculations, so both of these methods for calculation share a flaw. When calculating mechanical forces, forces are resolved trigonometrically. If the gravitational field is presumed parallel, you end up in a situation where this simplification implies no work is done in elevating mass (my example with Archimedes beam is making the same point, except there, the beam is resisting the weights sliding to the centre with friction adding a compressive force to the beam. Parallel gravity would mean the weight isn't trying to slide on the beam at all). With separation of particles, a compressive resultant force develops and the downward resultant force on the centre of mass diminishes. To be clear, the downward and compressive forces are resultant because I'm imagining this triangle as a pair, making them isosceles. The active force in response to gravity is on the hypotenuse pair. And then you simply plug in the dimensions, nothing complicated at all here. I hope that addresses your question regarding quantifying values. You are correct in that reactionless drives have nothing to do with this! I'm relieved you understand this.

Markus, the philosophical definition correction doesn't prove anything here, but it's noted. Gravitational fields propagate with mass radially. If you don't like propagate as a word, fine, I said it. You haven't answered specifically, you've just made an assertion. Try the maths, you'll like it if you know how to do it.

Thanks for the question swansont I mention apparent weight in combination with closed systems because these are the two main reasons people take issue with what I've written. Apparent weight is defined clearly: https://en.wikipedia.org/wiki/Weight Closed systems are what people use correctly to strike out what are known as reactionless drives, that is drives that somehow propel themselves forward without pushing something the other way, such that they break Newton's 1st and 3rd laws. I'm talking about orbit modification without rocketry. I'm not sure what you mean by an evenly operating force. When modifying orbits, the forces aren't even, that's kind of the point. Can you explain what you mean? I read I'm limited to 2 posts on the first day, so I'll address your other questions here. I have designs to show, I'm happy to upload them, I didn't want to be too much of a bull out of a gate, the post is long as the other reader noted. I've tried to give everything relevant so people can digest it. The case that I have explained identifies Iron Man and his mech double tethered together as the device. I've done this because I think it explains the physics best and the example works well. My point about closed systems is that when considering gravity, there's obviously no such thing. All you can do to keep the maths simple is to ignore negligible quantities so you can treat such examples as a closed system. In these cases, it's not so much a case of ignoring gravity, it's a case of presuming gravity to be constant and uniform (parallel), when it varies radially. This principle is at the core of what I'm presenting.

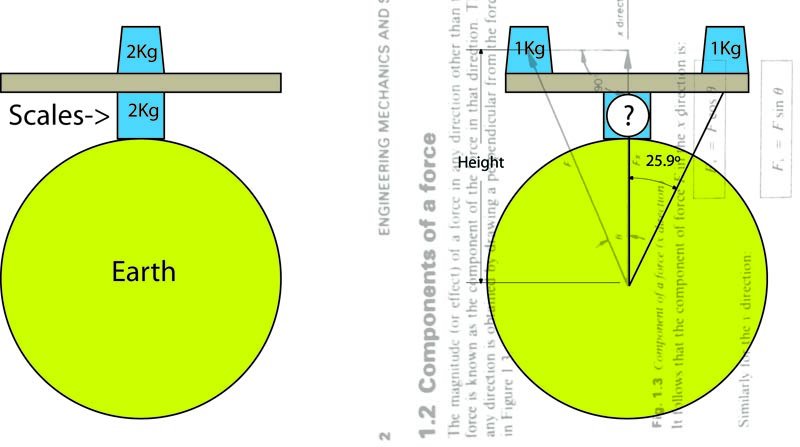
I am here today to post details of a design for an Anti-Gravity Drive and ask this question: Does the Anti-Gravity drive as described defy the laws of physics? The work has been viewed by no less than eight professionals in the field. I believe some of these professionals only took a superficial look at the work, but some of them were required to take a fairly deep dive. To date, none of them have been prepared to identify specifically the mistake that I’ve made which has led to what is asserted to be an erroneous conclusion. As a designer, if there is no reason not to proceed, one proceeds. Failure is an unavoidable feature of design. Depending on how you fail as a designer, it can harm your future prospects, but often it’s a case that there was no way of knowing how a design will fail. At this point, it’s important to point out that I can’t get a formal peer review, because I’m not a peer. As a wise man once said “I’m not a maths surgeon”. It’s not important right now to detail where my experience came from, to be able to contemplate this problem, but I am a practising designer and pattern maker. I’m technically qualified to make stuff, have a keen interest, a broad knowledge base and my judgement about what can be built shouldn’t be dismissed without a solid argument. The design is simple. The way the device needs to modify its form requires very little design skill to create such an operative device. That aspect of this project is not what I’m here to discuss, at this point. I am simply here to get some opinion, positive or negative, but hopefully supported by evidence. I can’t really do anything with unsupported evidence, so negative unsupported opinions will not influence my decision to persist. As it stands, I believe the level of maths required to model the performance is what you might encounter in high school specialist maths classes, certainly at a level that would be expected of someone entering their second year of a related specialist degree. I have been working on this problem for much longer than it usually takes to for someone to acquire the skills to solve the problem and I am invested in finding an honest answer. The following description is divided into two parts. Part 1 describes the idea and the basic kinematics of Anti-Gravity drives using examples and references to the methodology one would use to predict mathematically the basic behaviour of these prospective devices. Part 2 features ideas that I don’t think are patentable, or are otherwise disclosed so they cannot be patented. This is also why I’m not going to fully detail or address many of the issues that will come up if and when it comes time to attempt to put these ideas into practice. The calculations I have made in Part 2 are very much back of envelope calculations that I haven’t thoroughly checked, however, I’m pretty sure things aren’t out by orders of magnitude. This is a personal time and resources decision. Part 2 was written before observations regarding energy were brought to my attention, so it’s lacking insight in terms of how we view the scenarios with respect to energy. It also appears that the material in Part 2 will be more difficult to describe than in Part 1 with respect to energy. People are invited to explore these concepts. I think I’ve made a solid starting point for this, however, anyone taking it further will need to understand compound functions and the integration of these functions over time. Following Part 2, I have a few statements which will hopefully assist people in conceptualising these new ideas. There are three PDFs to view which provide further detail and calculations. I’m having trouble uploading these, I will try to make them available as soon as I can. Please forgive any disjointedness through this material, this is a developing idea. I have a limited amount of time to get the proof I need to have a chance at being remunerated for this disclosure. I believe it won’t be long before I can collate all of these ideas with the help of people suitably qualified into a more definitive and easily digestible form. Part 1 I want to talk about apparent weight. And I want to talk about open and closed systems. We have some loose definitions in physics, and I would like to identify these that I think have stymied us for too long. When talking about orbiting structures, we generally consider these structures to be closed systems because gravity is presumed to be operating evenly across the structure *in the one direction*. This is an estimation, based on the application of the definition of weight. Consider this carefully: in a “closed” system of a stably orbiting structure, apparent weight is presumed to be a property that can’t be changed. I have dealt with experts who misconstrue this specific scenario in this way, or at least, their assertions lead back to this erroneous view. The view is that it’s impossible to change the apparent weight of a structure in orbit (without rocketry) because it’s a closed system. First of all, if we are talking about apparent weight within a closed system, a prime is and must be part of this system, given that weight is a property acquired by mass through gravitational attraction. Secondly, gravity is a force that propagates radially, therefore, with any separation distance of points within a structure, gravity will affect all points in slightly different directions (or with slightly different magnitudes - all points of a structure experience slightly different gravitational forces relative to the prime). If the separation is a difference in altitude, there will be a tensile force. We see this everyday with water flowing from a tap. The lower water is attracted slightly more to the Earth than the higher water. I believe the extreme example of this is known as spaghettification. (Quick spoiler - consider this with respect to accretion and the directional bias of the inelastic collisions further on - double spoiler - I expect the electromagnetic interactions (inputs and outputs) to attract a lot of interest). If the separation is in the direction of travel, sufficient velocity may counter what would be a compressive force, which is what happens at orbital velocities. This compressive force, however, is fully apparent in separations of uniform elevation and in directions orthogonal to the orbital plane. This force is fully apparent in all directions except for the (localised) direction of pure gravitational tension, which is co-linear with the gravitational force. And here lies the conundrum. The simplified method for calculating apparent weight implies that this compressive force does not exist. However, it can be plainly shown that this force does exist and that the simplified method for calculating apparent weight breaks down readily. The simplified method for calculating apparent weight implies that gravity is uniform no matter how far a part of a structure extends beyond the centre of mass and the gravitational field line running through it. Consider this: my homies and I borrowed Archimedes’ big lever, I promise no coercion was involved whatsoever. Anyway, we shall say his lever is now a beam supported in the middle by a scale. Now we zero the scale. If we place 2Kg in the middle, the scales read 2Kg. Now we take 2 x 1Kg weights. The simplified apparent weight formula tells us that it doesn’t matter how long we stretch the beam and how far towards the extremities of the beam these weights are placed, the scales will still read 2Kg. To me, this is as absurd as I felt it was when it was first taught to me. Correct me if I’m wrong with cold water and the full force of a firehose, I don’t see any reason to treat gravity differently for resolving forces than one would treat mechanical or electromagnetic forces. Therefore, it should be seen that with greater separation distance, the scales will read lower than 2Kg. When the beam reaches the width of the diameter of the Earth and the weights are on each end, the scales will be reading about 70%, or inverse the square root of 2, given the weights are now 45º offset from their original mid position. At this point, the downward force on the scales is also equal to the force required by the beam to keep the weights from sliding towards the centre of the beam and each other. The beam is resisting gravitational compression. From this example, one should now be able to identify how you can have two particles act on each other with the reaction involving an increase in altitude of both the particles, irrespective of the centre of mass which obviously doesn’t change..... if it’s stationary. Double take on that: It is possible for two particles acting on each other to ascend. There is no need for anything else to be involved other than the prime. The prime will respond to this action, but it can’t stop it from happening. All the prime can do is provide its usual gravitational resistance which simply requires work to overcome. Additionally, using the simplified method for determining apparent weight, no work is required to elevate particles in this way aside from the initial acceleration which, as asserted by this rule, returns this work energy when the particles halt. Pull the other one, it plays jingle bells. Let’s depart from this example and move to an application of this. Iron man and his mech stunt double are in orbit and are about to do their anti-gravity stunt. They’re going to do some eccentricity pumping to start. They are also tethered to each other, so you might consider them a whole body. (I think at this point it could be useful to make a distinction between a closed system and an isolated system, where an isolated system could still be said to have a meaningful definition of apparent weight). They align themselves ready to do a mechanically assisted jump, so that they push each other as far from the orbital plane as possible. Then they jump, converting some form of stored energy into kinetic energy. So what will happen? Since they both have added kinetic energy to themselves, their orbit will be enlarged. The period will also be lengthened. For those now raging at this supposed heresy, get out your vis-viva formula and do it. Find A and B of the original orbit and the new orbit. Adding kinetic energy enlarges the orbit. There should be nothing controversial about this at all. There is no magical thinking. Check the attached document for how I believe I have proved this. Downey and his mech buddy pushed each other apart. Their orbits enlarged. Yes, there was an angle shift, however if the value of B is investigated mathematically and considered conceptually and Downey and his mech buddy are considered the one body with one centre of mass, the B value of their new orbital ellipse must be larger even after the counter angle shifts are rectified. This makes sense because orbit is a special condition far more like a race car hugging a corner at the limits of tyre friction, versus the oft used ball on a string analogy. The ball on the string is bad because gravity never increases nor decreases its force, whereas a string does and responds with extra force to the type of load modification being proposed. Taking the better analogy, the original orbit is the most extreme case of trajectory deviation caused by gravity. Any increase in elevation or kinetic energy of the orbiting bodies will mean that it takes longer for gravity to apply the same change in direction than for the original orbit. This is why both A and B are enlarged - it takes longer for the prime to apply the change in direction to the orbitals. Because it takes longer, the orbitals travel further and reach an altitude higher than had the separation force action not occurred. Once again, correct me if I’m wrong. With respect to energy and its conservation, Downey and co are not contravening any physical laws that I’m aware of. OK, so where are Downey and Co headed? Right back at each other at apogee. At apogee, they have a choice - if they don’t do anything, they’ll probably dodge each other because real world. In an ideal example with perfect trajectories, they will collide. I’ve heard orbital dynamics analogies similar to this referring to particles returning to the scene of the crime, however, interception occurs at both apogee and perigee in an ideal system. So if they dodge each other, they will again diverge and re-converge at perigee. In the real world, they will most likely dodge each other, however, they can both pull on the tether binding them to cause an inelastic collision. This will not be a perfect collision, although in an ideal system it would be. The slight divergence from the ideal will cause a little rotation to be imparted on the system. I don’t want to get hung up on this rotational energy at this stage, but I most certainly am not ignoring it. Let’s imagine the collision in the ideal scenario. Downey and his mech double pushed each other apart, imparting a certain velocity on each other. When they inevitably collide at apogee, they will be travelling towards each other more slowly than when they diverged. Therefore, the inevitable collision will transform less kinetic energy than was originally imparted by their jump. Because energy is conserved, it should be obvious that there must be a remainder of orbital energy from the original jump that persists in the system even after this inelastic collision. So at apogee, there are two main possibilities as to how the system proceeds. If they dodge each other, the system will retain the orbital energy created from their jump. They will return to the scene of the crime at perigee and continue to dodge each other cyclically at perigee and apogee. If they withdraw energy at apogee via an inelastic collision, they will be at the apogee of an orbit, but they will have insufficient kinetic energy to return to the scene of the crime at perigee. The perigee of the new orbit will travel to a lower perigee than the original orbits. What has happened is that Downey and co have entered a higher energy orbit with greater eccentricity from the original circular orbit. The highest energy orbit here is the orbit taken when they jumped apart. If we were to draw an analogy with an internal combustion engine, this is the power stroke. The orbit following the withdrawal of energy via the inelastic collision could be likened to the exhaust stroke, which consolidates the system that now has a higher energy state. Repeating this process creates further discrepancies between the energy inputs and outputs at apogee and perigee, meaning the action becomes more effective. This is eccentricity pumping. Eccentricity pumping can continue until physical proximity of the prime prevents any further pumping. Anyone following up until now should be able to see that Downey and co have added to their orbital energy from their own stored energy. A cynic who follows will rightly say the amount of energy being imparted is two-fifths of naff all. And to an extent, they would be correct. So now to the cynics who would indeed be on the ball, how can we get more out of this? The simple answer is to invest more energy into the jump. That’s true, but this doesn’t solve to increase the maximum extent of orbital pumping, adding more energy will just bring the bodies closer to terminating on the prime sooner (assuming the jump didn't achieve enough velocity to escape to another gravitational system). There is also that problem of the length of the tether binding Downey and Co. With more energetic jumps, they will travel further away from each other. While the tether is unnecessary in the ideal example, in the real world, we want the tether, because Downey and co are intended to be acting together. Which brings us to the next stunt. This time, at the 90º position of their post jump orbits, they will intercept a large object, large enough that they can plant a big mawashi geri simultaneously onto the large object. Let’s say Holly stuffed up the navigation again and the Red Dwarf ended up a little close to the Earth. They will push the kick in the opposite direction of gravity relative to their shared centre of mass. This will cause the Red Dwarf to be propelled upwards, and Downey and co will be propelling themselves downward - on a trajectory perfectly mirrored across the orbital plane about a line running between the prime centre and the kick point. This situation now gets very ugly. Downey and co did a full equal and opposite force action number on the Red Dwarf. They send themselves back to the orbit from whence they came. The initial jump energy can be withdrawn fully. There is energy applied to the large object. We have what appears to be a breach of conservation of energy. There is no breach. What really has happened is that when Downey and co did their jump, they had the energy to complete a nice big orbit. However, they took the potential and kinetic energy they added in their jump and put most of it into the Red Dwarf, effectively stalling their orbit in a manner causing them to end up following a mirrored trajectory back to their original orbit. A good way of describing this is contrary motion. The energy that has seemingly appeared is reflective of the period change. Eccentric orbits out of phase with each other feature massive relative energy fluctuations. This fact still doesn’t explain how more energy can supposedly appear. The answer to this I believe is to with the signage of the potential energy. It certainly does take a lot of energy to move objects in the opposite direction of gravity, but I’m pretty sure in terms of the signage, a high energy state is one where objects influencing each other gravitationally are close and the lower energy state is when they are further apart. As bodies are progressively ‘forced’ away from each other, it requires increasing amounts of energy to bring them back together. The energy that seemingly appears from nowhere is actually stored energy that existed prior that is gravitationally bound. Much of this energy would presumably be accretion energy bound during the formation of the Earth.The bodies are losing their gravitational binding energy. This could be analogous to a deflating balloon. The state of close proximity is high energy like an inflated balloon. As energy is released, the balloon goes flat. Likewise, the acceleration away from the prime releases this stored energy energy bound by gravity. However, we tend to view these things up side down, which works for most instances from a lay perspective, except obviously for this instance when strange energy appears seemingly out of nowhere. I believe this also relates to why kinetic and potential energy have opposite signs for when calculating orbital energy. I believe they lay perspective also mostly works because it’s not necessarily wrong to be viewing energy to be either negative or positive, what’s important is that the signs for KE and PE are opposite. This aspect may be better explained by someone more familiar with these conventions, assuming that I’m correct in a roundabout way. To bring this explanation back to energy conservation, energy is simply withdrawn from the system. To restore the system to the original state, one must reverse this kinetic energy to bring the bodies back to the prime. It also helps to remember how all of these motions also cause the prime to move and change course. Also, relative to the rest of the universe, the gravitational pair have the most gravitational influence on the rest of the universe when travelling together than when they are travelling in different directions, given that amounts of kinetic energy are neutralised if the bodies are travelling with different headings. I believe that the slight variance in the gravitational effect on the universe of the distanced gravitational pair reflects this loss of energy, as does the slight loss of compression in the gravitational system, these things being the opposite sides of the energy coin. Delving a little further into what is my speculative but best explanation, as the original gravitational pair are separated to the extent that the local gravitational normalises such that the attraction between the pair is rendered null, if they still have velocity, they will commence accelerating away from each other upon the assumption that the only diminishing gravitational force the universe is supplying is what remains between the original pair. This might also be seen as entropy regaining the upper hand. Without risking ruminating on this much further, as there’s a lot going on here, another factor to consider is that we mostly encounter stored energy stored gravitationally as compression. If the force of gravity generated by the Earth suddenly disappeared, it would be just like releasing a spring - everything would suddenly spring out and anything not tied down would head off into the wide yonder. In the case of the action being described by this post, this action is forcing the prime’s gravity to work against itself to throw a spanner in its works for long enough for some displacement to occur. Let’s put a twist on this. It seems I’ve found a source of free energy. We can pitch it to the free energy crowd. Have at it! Take as much as you want! Off ya go! Seeya! They will then proceed to sail off into the universe. However, if they want to come *back*, they will find they were quite dependent on that energy keeping them in the manner accustomed. They will need to reverse their kinetic energy to turn themselves around. Then we can remind them that while energy is conserved, the price of energy is *not*! Mwahaha!!! My apologies for any drinks spilt! Part 2 The manipulation of weight within a ‘closed’ system does very little on the Earth’s surface. However, in orbit, I will show how the manipulation of form and weight can effect a useful method of propulsion. Returning to the specified revised method of determining weight, seeing a body as a divided structure with two centres of mass acting on each other and being acted on by a prime provides a rough estimation for the dynamics of any rigid structure that can be mathematically simplified and represented as a divided structure with two equal constituents. For those not following the spatial relationships I’m inferring, what is being considered are very large structures where the radial nature of gravity can be utilised to effect propulsion. Fabricating structures at a useful scale would most obviously involve tethers, however, useful rigid structures or combinations of the two aren’t necessarily useless or impossibly large to build. For use within Earth’s orbital space, rigid structures would probably not be practical. However, the useful application of such a propulsion method while orbiting our moon or other smaller prime may not require a rigid structure beyond our fabrication capabilities. It’s easy to see how tethers would be a far more useful application of this propulsion method, however, the dynamics of motion are more complex. For simple propulsion, two masses coupled with tethers can be propelled in directions equal and opposite to each other and away from the initial orbital plane. Ideally, this action is perfectly balanced, meaning that the centre of the tether remains on the initial orbital plane. In the case of a rigid structure, the rigidity prevents drift between components. Assuming any spacecraft utilising this propulsive method within a rigid structure has sensibly placed gyroscopic elements, the attitude of the structure can be controlled so it doesn’t become cranky and unwieldy. Therefore, the motions of a rigid structure example can be described by splitting the structure into two equal sides and calculating the gravitational forces acting on both sides as the spatial mass balance is manipulated. For a tether based structure, motion is used to define the structure. This approach is useful because the attitude is effectively embedded into the motion. A rigid structure may need to activate its gyros continuously in an effort to maintain attitude in response to micro gravitational effects, but there is very little these effects can do to prevent masses bound by tethers from being sent where needed to effect propulsion. As mentioned earlier, a tether based system will experience drift of its constituents as an effect of the propulsion method. The centre of the tether will try to maintain its original trajectory that it effectively shared with the rest of the propulsion system constituents. However, when the bound masses are propelled away from the orbital plane, they will recede relative to the centre of the tether which remains on the orbital plane. Consequently, the tether will have extra tension applied to it as it proceeds relative to the bound propelled masses. This drift can be accounted for by providing a slight amount of force to the centre of the tether so it is made to recede, while the reaction of this applied force causes the propelled masses to proceed, ideally enough so that the amount of drift is limited. This drift is something that requires a great deal of analysis and I definitely don’t have complete solutions to this problem for every scenario at this point. What I can say is that the effect of drift will basically present itself as the outcome of the compounding of constituent orbital ellipses. At the most simple level of analysis, calculating drift will require dividing the structure into three elements rather than the two for a more simple rigid structure. The addition of a central mass provides a basis for this. At some point, drift becomes excessive and terminal, however the effect of small amounts of drift on propulsion efficiency is not well understood at this point. As further detail is described here, it will be shown that kinetic and potential energy can be manipulated to effect orbital dynamics and orbital energy can be stored as tether tension and ‘stashed’ away to be released at will. It’s not clear if the tether tension created by the drift is diminishing orbital energy. It is possible to counter most of this tension by limiting drift, so I don’t believe drift will present challenges that rule out the use of such a propulsion system. At this point, hopefully I have detailed my idea to prove that it is physically possible to internally generate a propulsive force without expending propellant. I have prepared a PDF presentation that details simple calculations for determining how much force can be provided by an endowed structure at a particular scale. What the presentation also shows is how this force can be applied theoretically and includes scaled examples. Following the PDF is a slide showing how the Anti-Gravity propulsive method with an extension distance of about 950Km can raise a payload in orbit and how it compares to a rocket performing the same task. As noted at the beginning of this explanation, this solution is ugly. It needs to be large so is therefore difficult. The motions require heavy duty mathematical analysis and the propulsion method does not provide simple point and push propulsion which rocketry can provide. However, if the propulsive motions are understood and we can agree on how we can best provide the possible benefits, there is opportunity for mass transit to be reimagined. Intercontinental travel may be more economical 100Km up. This brings us to the aspect that will hopefully have you sitting up if you aren’t already. I’m sure some will be roughing quantities in your heads thinking this idea might be possible, but it’s probably too feeble to be useful. Place your seat in its most upright position. The exit trajectory. Through my research into this project, I was presented with two NASA papers from the 1990s. Let’s call them D2 and D3. They describe basically the same thing and are by the same authors. It appears that the later document is an updated version of the earlier document. D2/3 basically describe a tether based system for relocating satellites. The system is a practical approach which uses rocketry to generate unusual responsive forces that can be used to move satellites around. Without necessarily being dismissive of their work, I think there are problems with it. They have claimed that this type of structure can generate propulsive forces without expending propellant, which is actually true, but there are serious caveats to this that they have not mentioned. What is unfortunate for Laris and Hratch is that they did not consider the effect of propelling masses bound by tethers away from the orbital plane. What they did describe is the deployment of a tether by allowing it to drop from a body in an initial orbiting position and performing manoeuvres with a payload. They describe orbit eccentricity pumping, but I believe they have the wrong end of the stick on that one. What I believe D2/3 represents is the antonym of the Anti-Gravity Drive, the Hyper Gravity Drive. The HGD can apply a force in the direction of gravity. This might not be as useful as the force generated by an AGD, however, pushing an object in orbit downward has been considered just as practically impossible as pushing an object in orbit upward without the use of rocketry. How a HGD generates a downward force is explained along similar lines as how the AGD generates an upwards force. In essence, masses are separated for gravity to exercise different forces on them. As gravity is a time based force as well as a radial force, optimisation of this effect requires vast separation distances and plenty of time for gravity to work. You can’t throw cake mix into an oven and expect it to cook quicker than usual, particularly if you can’t turn the oven up. The propelled masses need time to accumulate the desired velocity changes. In both the AGD and the HGD, the resultant velocities of the masses are cyclic. Indeed, any orbiting body has a cyclic velocity, but these drives have an extra cycle, which involves the relationship between the two masses relative to the prime. The quirk of the AGD is that the cyclic oscillation of the two masses does not cause them to go out of phase. Instead, what the AGD does upon expansion is the amplification of both of the A and B components of the orbital ellipses of the masses. The resultant orbital ellipse of a body endowed with an AGD exhibits these amplified proportions. For the HGD, the masses (which have different elevations) in theory oscillate in an out of phase. In reality, the tether strikes the prime. By separating the masses without deviating from the orbital plane, the masses accelerate differently and diverge. If they were not connected by a tether, they would shift in and out of phase relative to their orbital periods. Therefore, a HGD can’t be left to cycle, the separating action must be countered before the masses become too far from each other or to prevent the tether from striking the prime. At this initial stage, orbital energy is lost by being converted into diverging kinetic trajectories. The initial separation of a HGD only requires work to bring about the initial position. Once deployed, a tether will extend itself as it travels downward. It will also proceed in orbit relative to the deployment platform. For the tether to be retracted, work is required. Retracting the tether adds orbital energy to the system, and the variance in the velocities of the two masses can be negated. Or so it is alleged… While I don’t as yet have numerical proof that this is impossible, I have a very strong hunch that this is impossible. Specifically, when the tether is retracted, the force acting on the two masses can only be in line with the tether. I think it will be impossible to bring about a situation using retraction from separation where the resultant trajectories of the masses closely match each other as much as they did initially. Mismatching velocities will result in rotation. This rotation is obviously kinetic, but it is an energetic fluctuation that provides effectively no contribution to orbital energy. This is handy if you want the drive to cause descent, however rotational energy is an attribute undesirable for most other purposes of these drives. Even withdrawal of orbital energy via inelastic collision is made difficult or impossible by the effected rotational kinetic energy. What I believe is possible when utilising a HGD is contrary motion. When the tether is retracted, the mass that has acquired a lower altitude will be decelerated by accelerating the trailing elevated mass. With some mighty reeling action, the lower mass could be dramatically slowed down while retaining its initial circular orbit, with the elevated mass being pulled from its circular orbit into a massively accelerated trajectory that rapidly approaches the lower mass. When the two masses reach their closest proximity, the rotational energy would become evident if the tether is locked. In this case, where the trajectories of the two masses are parallel and the lower mass trajectory remains tangential to its initial circular orbit (albeit much slower), the HGD begins traversing an elliptical orbit smaller in magnitude than the initial orbits. Both A and B components of the ellipse/s are diminished and the position when the tether is locked becomes the apogee of such an orbit. This motion provides the capability to push another object downwards. While the contrary motion of the HGD is not perfectly contrary like the AGD, it’s not far from it. All that needs to happen to create the contrary motion is for the rotating HGD to apply its rotational force downwards onto a desired object such that the rotation is reversed. The resultant trajectory will then resort to motion contrary to the initial trajectory. This is very much a case of an action having very much an opposite reaction. Therefore, the HGD can provide a useful force in the direction of gravity. However, the HGD and the concept of contrary motion have one more play. If the retraction of the tether is followed precisely by a re-extension of the tether in exactly the opposite way it found its way to the perigee, the system will reverse the initial actions and be restored to its initial state. The utility of this set of manoeuvres might not be immediately apparent, but if you’re looking for a safer way off this rock, here it is. In this situation, the lower mass of the HGD can be decelerated substantially. This makes it an ideal platform to capture or assist a suborbital space craft and accelerate it to orbital speed. The reverse is also applicable, meaning that an orbiting body can be substantially decelerated prior to re-entry, meaning that heat shielding does not need to be as substantial as is required for re-entry directly from orbital velocity. In a nutshell, this is how I can envisage potentially the removal of two significant figures from the full requirements for orbit. If rockets are only needed to elevate rather than stupendously accelerate payload, then they don’t need to be anywhere near as big. Shrinking them down by a factor of 10 relative to their payloads appears to be very achievable. It remains to be seen if its possible to have an exit trajectory with no lateral movement, but If it is possible, the fuel requirements should be reduced to approaching 1% of what is currently required per unit mass. I will note that my back of envelope calculations for this also include a massive ramp that in theory can be used to accelerate a suborbital spacecraft prior to the spacecraft firing its own engines, in essence, giving it a head start. There is also scope to apply one more element to this system to further reduce the velocity of the exit and re-entry trajectories. This element is a tether with a varying diameter, like a bullwhip. The physics of the bullwhip form is useful for space tethers. It is presumed that the bullwhip functions by transforming a wave with a large mass and small amplitude into a wave with a small mass and a large amplitude. The large amplitude is what causes the tip of the whip to break the sound barrier. In the situation of orbit, the bullwhip tether design will be used to decelerate the tip so the tether and the rendezvousing spacecraft don’t intercept at ridiculous velocities. The distinguished NASA researchers may have conceptualised all of this, however, without a method to accelerate a payload that doesn’t rely primarily on rocketry, the point is entirely moot. However, when the higher mass of the HGD sweeps by the lower mass at a substantial clip, well above the initial orbital velocity, here presents the ideal scenario to activate an AGD. The considerable utility of decelerating the lower mass yields the considerable utility of a massive velocity of the the higher mass which will greatly assist an AGD attached to the higher mass. At this stage, it should be clear to people who understand how orbit is achieved conventionally, how an AGD and an HGD can be used in combination to reduce the required exit velocity. However, it will also be clear to these people that the velocities involved are massive, and the relative intercept velocities can also be massive. Reaching and changing velocities of this magnitude requires massive transmission of forces. If structure destroying impulse/G forces are to be avoided, the transmission of these forces needs to be conducted over long periods of time. For the transmission of forces to be conducted over long periods of time, the tethers need to be very long. It takes very little scratching around at these requirements versus our limited selection of materials to see that some very hard limits will apply. I believe initially, steel tethers could provide sufficient strength to achieve some level of utility. A steel tether of uniform diameter can hang a little under 30Km down from low Earth (geostationary) orbit before it yields, further if the diameter varies. However, adding load will obviously diminish the possible hanging distance. I don’t envisage hanging to be a state often used for space tethers, however, when reeling in a tether or opposing its extension, the hanging distance is indicative of the amount of force that can be applied through the application of tension to the tether by reeling. If applying a force of 1G to the tether, then the maximum distance of the tether will be roughly the same as if it were hanging straight down from its platform. If you need 2G, the possible length will be approximately halved if the same gauge tether is used. In this specific situation, the mass of the payload would also need to be halved in order to retain the specific proportionality relative to tether yield modulus. Using the formula for displacement relative to velocity, time and acceleration (s = ut + 0.5 at^2) it is possible to calculate the amount of acceleration that is possible to be applied over the length of the tether. A simple example including a load could see a tether mass double that of the load. At 1G, this would resolve to a tether length of 20Km with the final 10 Km that is possible for an unloaded tether substituted for a load. To provide 2G of acceleration to the load, it is simply a case of halving the distance and mass of the tether and the mass of the payload. Using rounded numbers, s = 10,000m a = 20m/s u = 0 The time taken for the tether pull is therefore about 31 seconds. Feeding the acceleration value back into the calculation yields a final velocity of about 630 m/s. This means that for a rocket launched from Earth that can be tethered in LEO, the escape velocity requirement is 630 m/s less. This hacking away of the escape velocity requirement is especially helpful for the final stages of an exit trajectory because it takes increasing amounts of fuel to achieve acceleration as the velocity increases, the same way a car engine labours as the car reaches its maximum speed, or the way one’s foot can’t push back any faster on a skateboard when one’s maximum speed is reached. The accelerative capability of such a tether system is therefore tied directly to the strength of the tether material. Higher accelerations require the tether to be shortened or strengthened, with the final velocity being largely unaffected by the by the acceleration value used if a tether of uniform thickness is used. It is therefore advisable to use a tether with a varying diameter for this reason as well as to produce an amplifying wave of motion through the tether as perviously described. It should be noted that the tip of a tether that decelerates as it approaches the target payload intercept point is being pulled down by gravity and experiences increasing tension as a result. However, most of the tether remains travelling at orbital velocity or near orbital velocity. This means that the (uncountered by velocity) gravitational load is concentrated near the tip, so is relatively insignificant and the stress experienced by the tether is primarily due to the application of force to itself and the payload. Therefore, even a steel tether in orbit can be exceptionally long if well designed. Due to the squared relationship between cross sectional area and physical strength, it is therefore better to create longer tethers using reduced acceleration values to achieve the maximum acceleration of the payload relative to the tether material. Calculating the maximum capability of a steel space tether system we could build using existing technology is one of the most immediate priorities for this project. Hopefully this very basic analysis illustrates a real potential for operability. If we’re able to fabricate graphene even to a tenth of its theoretical maximum strength, it should be entirely possible to elevate a payload to arrive at the vacuum of space with negligible velocity. This case represents the low end of rocketry requirements with any further reductions requiring a dangling tether to encounter the atmosphere. With increasing tether strength it becomes possible to dangle a tether further and further down into the atmosphere. It may well be possible for a space tether to dangle all the way to the ground as its platform is suspended in a geostationary position at a low Earth orbit elevation. The suspension can be provided with sequences of AGDs that continuously cyclically generate enough upward force to suspend the tether platform by applying this force to the tether platform. Connection Coupling payloads and tethers is not a particularly difficult feat. Manipulating and positioning tethers can be achieved with rotational motion applied from the tether platform or anchor point, as can the initiation of a bullwhip manoeuvre. With expertise, the positioning of tethers would be achievable with accuracy within a few hundred metres. A suborbital spacecraft could rendezvous and connect to the tether in a manner similar to the airborne refuelling of other aircraft. Alternatively, if the suborbital spacecraft can extend its own tether, it will be very easy to have the two tethers intercepting each other which can then be fixed together with magnetic devices interspersed in the tethers. If a stronger connection is required, secondary connection devices can operate once the initial magnetic devices are activated, as long as the tension doesn’t increase beyond the initial magnetic connection capability too soon. A lighter initial connection is possible because the tension of the applied load doesn’t reach its maximum until the connected tethers together form basically a straight line after intersecting at substantial angles. Scepticism of this aspect of such a system has been expressed, however I would counter this with the nature of tether type structures, which are common. Anyone who has dealt with cabling for various purposes understands how much unrestrained cables like connecting with each other. Turn your back on them for a second and they’ll wrap themselves around each other twice over. The main problems fairly unique to connecting space tethers is the potentially massive relative velocities and the transmission of static electricity. The static electricity transmission is more substantive with an extended tether, however, the transmission of the static charge is not continuous and this energy can be mitigated as long as the resistive heating of the contact points is managed with appropriate cross sectional areas to prevent any substantial loss of strength. Using tethers feathered with protruding semi-conducting strands that fuse or otherwise vaporise by design can also be used to mitigate the static charge. The relative velocities are also easily controlled as described previously. Traversing a tether A space tether can obviously be used to pull a payload. It can also be used as a pathway to be traversed like a train. Traversing a tether will be preferable to pulling and winding a tether if large velocity shifts are required. This is because there will be very hard limits on how fast a tether can be reeled, given that the reels will explode if they rotate too quickly. Traversing a tether with interspersed magnetic or electromagnetic elements can be achieved easily without requiring physical contact. This is because a maglev is easy control if the lev is taken care of, as it is in orbit. Large masses at termination points can provide the resistance required to enable large velocity shifts on a short tether. The Space Trapeze The final form of orbital space travel using the described tether systems will resemble a planet spanning space trapeze. Payloads can be elevated, picked up and tossed from structure to structure into higher orbits without the use of expendable propellant. Payloads for re-entry can have most or all of their kinetic energy removed so that heat shielding is not required and that massive loss of energy is entirely avoidable. Intercontinental travel will have travel times reduced substantially. Artificial gravity will be able to be applied by alternating acceleration and deceleration of tether traversing spacecraft. Cats and dogs will be able to tolerate each other and someone else will put your bin out for you. Everything will indeed turn out Millhouse. And did I mention our mini-golf and bowling scores? They will be great! Or my name isn't Pollyanna! Seriously though, these systems I believe are viable and could be providing cumulative returns on investments within ten years, probably sooner if we get busy. Also, if this technology is viable for use in Earth orbit, it will work spectacularly well when orbiting the moon, meaning colonising the moon will be a cinch and ideal for those with bad hips. Also Mars. But seriously, who’d want to go to Mars? Mars is a sh1thole. I’ve never liked anyone I met from there. The Path Forward I have undertaken this project with a moderate expectation of getting paid. This may not be possible for various reasons, however I have done as much as I reasonably can to position myself and anyone who would like to contribute to be able to develop this idea with the security of a time limited exclusivity. Yes, one of those. This means that I am personally contactable if one knows where to look. I would however appreciate retaining relative anonymity unless and until I am assured of some meaningful assistance to get this project off the ground. As I noted to begin with, I might be wrong. If this is the case, I would appreciate being able to disappear into obscurity to lick my wounds privately, content to leave these challenges to the professionals. If people out there would like to assist and don’t know how to find me outside of this site, I will of course contact them if I receive their details privately. This idea is fully disclosed. If it’s possible, it will go ahead, regardless of my ability to generate income from it. However, it will be a free for all if I am unable to secure the protection required to generate income, meaning that most of the benefits will flow to existing players. That’s the way the cookie crumbles. Time is of the essence and the possibility of substantial ROI is available and would be far in excess of what the existing players will be able to offer if it’s a free for all. Of course, existing players are absolutely invited to contribute and I would look forward to working with them to develop this infrastructure with a view of benefiting all of humankind. For those interested, I will disclose the status of the application so that they can understand the situation and the risks. I will make no claim assuring eventual success, any profits are entirely speculative at this point. However, in the scheme of things and considering the potential of this idea, the initial investment required to get the ball rolling is relatively small, so large returns are possible if all goes well. As far as I’m aware, I am the first to disclose this idea. If anyone knows otherwise, I would appreciate being informed. If anyone has any other reason to pour cold water on this, pour away. Over to you. Musings: I should be able to enter (with bodyguards!) a frat house with physics majors at 7am on a Sunday morning and find strewn among the bodies on the floor at least one physics major who, after being aroused from slumber with a vuvuzela, can tell me within 30 seconds what will happen to an orbiting body that has an external force applied. What’s the opposite of accretion? Is this not what you’re contemplating right now? Inversion is an extremely important feature for many fields, particularly for maths and music. If the problem is causing you trouble conceptually, try inverting it. Gravity is much better than no gravity. Is entropy an opposing force to gravity in the universe? What would happen if gravity was halted for a period of time? Would you call the ‘potential’ energy that appears “free energy”? Gravity did a lot of the equivalent of work to help bring our matter here for us to exist. Nature knows which way the signs should be. Tell me more about how the traditional apparent weight definition allows objects to be elevated without performing work/consuming energy. Anti_Gravity_Mathematical_Solution.pdf Eccentricity Pumping Diagram.pdf Orbital Interactions.pdf