Spectrum744

Dear Watson v. 3.0 (sn), I was thinking to invite you for a glass of wine (just kidding). Btw, do you mind if I call you Twiki?

Hmmm, is this a bot 🤖😳

What do you mean with contrived? What do you mean that they are not valid??

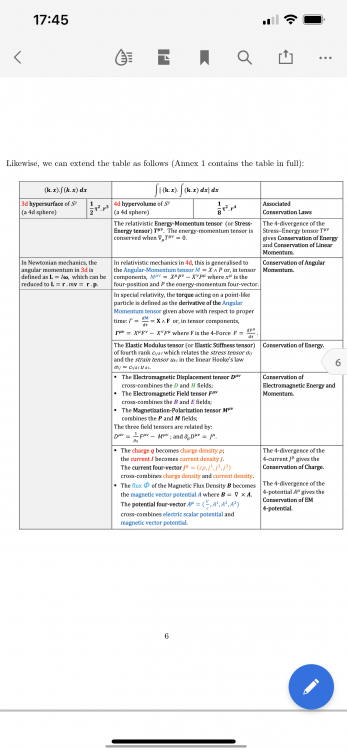
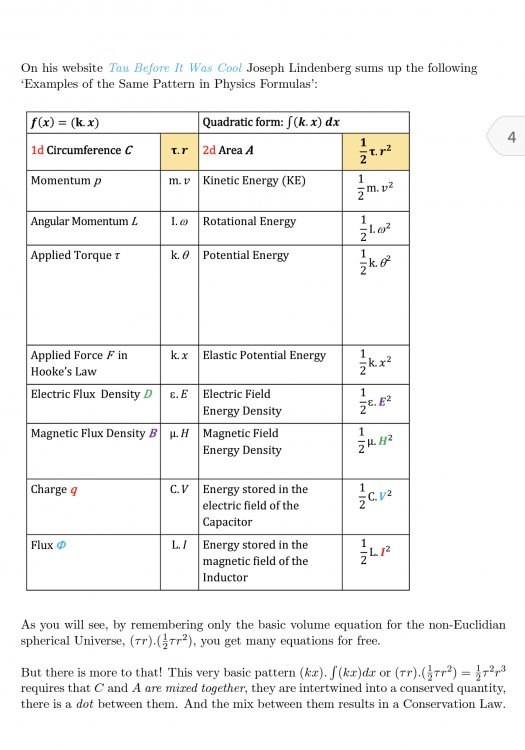
Well, ok, yes, but these equations all follow the same pattern and you can mix this up into ‘4d’. Einstein declares that the Universe equals 2pi^2r^3. Ok, fair enough, a bit strange vs. Einstein declares that the Universe equals a circle ⭕️ times the area of a circle 🔴 which corresponds to a pattern that can be found in many physics equations, which equals - multiplied together - the hypersurface and, and at the same time, this geometric pattern that these physics equations follow, is extended into 4d and corresponds to Conservation laws.

Indeed, if Q = m/2 then KE = 1/2mv^2.

It is just that I need at least like 20-30 pages to explain everything and I need also that you are willing to read the paper which I had attached, even only the first 5-6 pages. Unfortunately, I have the impression that you still haven’t done this. And I already explained that pi and tau will be continue to be used, but that is really of no importance here. Thus, for me it makes more sense to write a didactical explanatory paper for some curious student in the future. Luckily for me, some people have read and understood it and, as Feynman said, the pleasure of finding things out is more than a sufficient recompense 🤷🏻‍♂️

I’ve been thinking about this. The first pages of my paper are easy to understand but to understand the last part of my paper, where you start to mix e.g. 1d momentum (p = mv = τr) with 2d energy (K.E. = 1/2 mv^2 = 1/2 τr^2) and so on - and you thus immediately see why you need to use τ instead of π - into the 4d Energy-Momentum Tensor Tμν, you need to understand the tensors that are used in GR, and you need to be able to grasp (‘vizualize’) the difference between the 3d hypersurface and 4d hypervolume, something Einstein had clearly understood but which is not that easy to ‘see’. In the future I’ll write a didactical paper for the young (the easy part) and old (the part with GR and the connection between classical mechanics and quantum mechanics which appears visible). Pi will certainly continue to exist, Euler used the same term ‘pi’ for both pi and tau, but tau is certainly more elegant (as is the Dozenal system imo). Let me just hope that if someone comes along and understands my paper, (s)he senses a glimpse (Universe = ⭕️🔴) of the Beauty which good old Albert would certainly have seen too.

😅 I just have 5 minutes (need to run to school). I’ll try to explain it quickly. In Einstein’s 1917 paper on Cosmological Considerations etc (last pages)., and also in his book on ‘The Special and the General Theory’ he describes the Universe as 2π^2r^3 but that is a little bit an ‘ugly’ equation that doesn’t do justice to the beauty of it, namely if you wright it in terms of tau (2π), the same equation equals the Circle (τr) times the Area of the circle (1/2τr^2) which is a pattern underlying many physics equations, and which also give you the equation for the surface of a hypersphere. But I need to explain more (I’ll try to do this a little later), which in turn makes clear that the Universe we live in is the derivative-surface of its hypersphere’s etc.

(I’m working in between) thank you for your questions. 2πR = τR

Dear Swansont, yesterday I just stumbled on the Scienceforums.net while doing some research. Honestly, I just discovered it. I was really amused by, actually, your comments and I had the impression that you had good understanding of physics. This is the reason why I posted my paper here. Elegance and symmetry are underlying principles of mathematics, group theory, ... Let me cite Paul Adrian Dirac: "What makes the theory of relativity so acceptable to physicists in spite of its going against the principle of simplicity is its great mathematical beauty. This is a quality which cannot be defined, any more than beauty in art can be defined, but which people who study mathematics usually have no difficulty in appreciating. The theory of relativity introduced mathematical beauty to an unprecedented extent into the description of Nature." Unfortunately, why it is more elegant - in most cases - to use tau instead of pi cannot be defined. A French croissant tastes imo better than a croissant from country y, but I would have great difficulties to explain why, it is difficult to define taste. (As a sidenote, with respect to tau, I may suggest you to read the Tau Manifesto: https://tauday.com/tau-manifesto).

Your correct question should have been: "the substitution of the diameter for the radius" (see Euler's 1787 E7 "Essay explaining the Phenomena of Aire" where it all began, he still correctly used both pi and tau). It just make things much more elegant and understandable. I have attached the Pdf. After you've read it, please then come back with questions.

Einstein written in terms of tau (2π) makes a beautiful equation visible and helps to understand GR: https://vixra.org/abs/1805.0304. I hope someone enjoys. From the abstract: I propose to rewrite the volume equation for the non-euclidian spherical Universe in terms of tau (2π) instead of π. Written this new way, a truly elegant equation and deeper structure becomes visible. Further, I postulate that the Universe is the Fundamental Theorem of Calculus, i.e. that the 3-dimensional Universe we live in is the derivative-surface of its 4-dimensional hypersphere volume. 1805.0304v2.pdf