-
BSP offset ghost collisions
- BSP offset ghost collisions
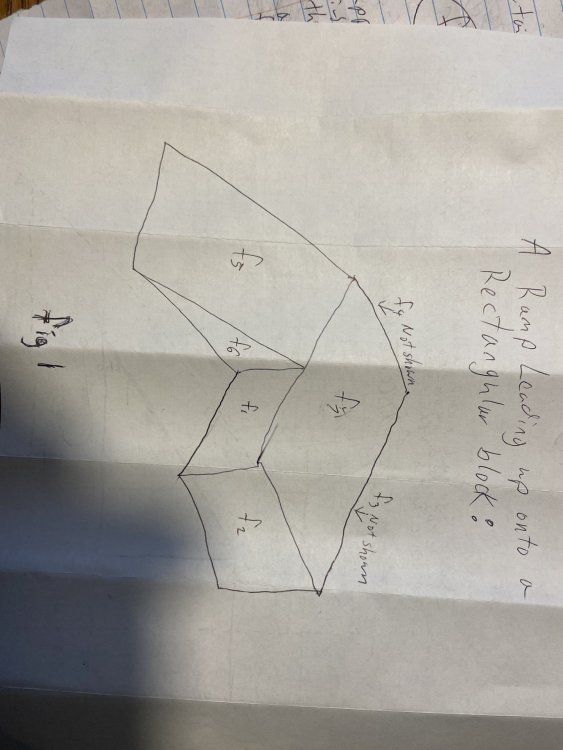
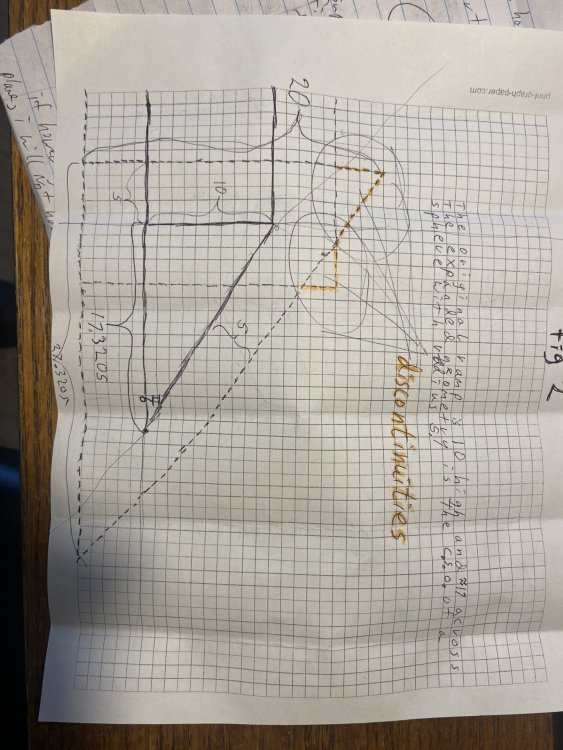
I am having trouble with bsp offset collisions. Certain topologies can cause this. For example: Suppose my bsp compiler chooses f1 as the first splitting plane. Then f4 will be split into a triangle (f4a) and a square (f4b). F2, f3, f4b, f7 will be "in". F6, f5. f4a will be "out" This is a bad bsp tree for collision detection using offset surface. The decomposition of the object into two convexes (a ramp and a block) will result in discontinuities that an avatar may get stuck on. If, however, I chose f6a as the first splitting plane, I will not have that problem because the ramp-block connection will be part of the same convex. How do I prevent this (and any generalization of this topology) from being compiled into a bad bsp tree? Beveling is not the problem, because you are only supposed to bevel if the angles are acute. The ramp-block interface is obtuse. Thank you.- Combining BSP/GJKEPA/PGSLCP algorithms into a Game Loop
I want to do the following; BSP offset as described by Melax in his paper for environment collisions. GJKEPA, or SAT for object on object collisions. Use collision response formula for bouncing objects. Use PGSLCP solver for sliding rolling objects. PGSLCP solver allows small inter-penetrations, which are corrected using Baumgarte stabilization. This means I don't have to subdivide time intervals every time a collision occurs. This works well with GJKEPA and separating axis, but BSP offset returns the exact time and location of the first collision. BSP offset requires subdivision of the time interval, because if the object falls through the floor an infinitesimal amount the contact will not register on the next frame. My question; is BSP offset incompatible with PGSLCP solver?- Projected Gauss Seivel Algorithm
As far as the face-on-face contact problem goes, I realize that I can't remove contact points willy-nilly. But it is important to make sure, each contact normal is facing the same direction. Sometimes they don't due to numerical issues. So, I remove contacts that don't face the same direction, as the normal returned by the GJKEPA. Sometimes objects will interpenetrate a tiny amount, and pop out on another side, resulting in a bad GJKEPA normal. This is particularly the case for very neat stacks. Messy stacks don't have this problem. But it seems as long as I used small enough time steps, this doesn't happen. Is this the correct way to do it? My next question: What is the best way to find contact data? When GJKEPA returns a normal end location, that is all I need to feed into my contact force solver, when one of the objects is a sphere. For polytopes this is not the case. I am currently going through all vertex face and edge combinations if a collision was detected. This seems inefficient. Also, I want the geometry of the objects to be consistent between collision and contact forces. But because I am using margins with collision detection, all the edges and vertices are beveled. Is it sufficient for the signed distance of the unenlarged objects to be negative or less than the sum of the margins? Thank you. I did not have a computer for a few weeks.- Projected Gauss Seivel Algorithm
I am using VSP trees. They also help with painter's algorithm. My problem is not with collision detection, however, but with contact force. Check out my last post about the optimization I want to use with PGS. Also, another contact force problem I am having; when I have a force act along a similar line but opposite direction of another force Baumgarte stabilization makes the termination criteria bad because the resulting acceleration is not 0 due to the contact force pushing objects away. This causes PGS to stall.- Projected Gauss Seivel Algorithm
Thank you. More to come.- Projected Gauss Seivel Algorithm
Update: I am now using Gilbert Johnson Keerthi with margins and expanding polytope algorithm whenever the depth exceeds the sum of the margins. No narrow phase, no binary search, much better. My next question is about an optimization I want to use on the contact force side. A sphere has only one contact point, but a polytope can have many. For example, a box stacked on another box has up to eight contact points. I know how to find location, signed distance, and normal vector. I want to consolidate these contact points into one contact force. Is it possible? Thank you.- Projected Gauss Seivel Algorithm
I have another question. It has to do with the interplay of collision detection and contact force. Is it possible to have GJK ignore collision points that are already in contact? I want to turn off collisions for these points and let Baumgarte correction prevent interpenetration.- Using GJK for collision detection
I successfully implemented GJK. It is fast, but narrow phase is a bottleneck because i do GJK many times in the binary search. I read about the EPA, expanding poly tope algorithm. Question: EPA returns the point on the CSO closest to the origin. Does this point correspond to the edge/edge or vertex/face to collide first?- Projected Gauss Seivel Algorithm
I successfully implemented GJK. It is fast, but narrow phase is a bottleneck because i do GJK many times in the binary search. I read about the EPA, expanding poly tope algorithm. Question: EPA returns the point on the CSO closest to the origin. Does this point correspond to the edge/edge or vertex/face to collide first?- Projected Gauss Seivel Algorithm
Thanks for the responses. As it turns out, I was incorrectly binding dynamic friction to equal zero if there was enough force to break static friction but still zero tangential velocity. If instead I just let PGS work its magic, the non-zero friction at each vertex cancels out so that an object at rest will continue at rest. Unfortunately, I don't know much about parallel processing on the GPU. But that will probably be my next step after extending to 3D. I suppose in a multi-player online setting the GPU can perform server-side computations such as if a grenade starts to slide or grow after bouncing a few times? Thanks again.- Projected Gauss Seivel Algorithm
I am using PGS to solve the contact force part of my rigid body simulator (2D for now). It seems to be functional but I can only seem to get a few decimals worth of accuracy. The algorithm will start cycling between different values. I realize that due to the lack of uniqueness theorem that there are many solutions to the NCP due to the introduction of friction. I want to find one solution that works and I feel that this cycling reduces accuracy. I tried subspace minimization but that doesn't seem to fix the problem. Fingers crossed that someone can help me. Thank You.- Baraff pivoting lcp
This is about the paper "Fast contact force computation for non-penetrating rigid bodies". Has anybody made sense of this? I have questions. Do I completely neglect the unprocessed a's that are neither mc nor c? If the sign for an unprocessed "a" changes, should I stop and pivot and put that index in either nc or c? I know that the unprocessed "f's" remain zero, but what if the sign of an unprocessed "a" changes? Do I actually perform a pivot operation on a matrix? Or is that done by moving between a "c" and an "mc"?- probability distribution of a function
I have a function y (x) defined over a range from x0 to x1 I want to know the probability that y will equal some number within a given interval if I choose a random value for x.- Statistics textbook
Now my son wants a statistics textbook. (for the uninitiated, I am only his humble scribe and mother). I remember my stats textbooks from 35 years ago in grad school (Statistics: An Intuitive Approach: Weinberg, George H.: 9780818504266: Amazon.com: Books), but they are not necessarily the best today. He wants one that will take him from relatively basic stuff up to regression analysis. If not one, then two in a series. Hopefully something that is inexpensive and/or available secondhand through Amazon. Suggestions? Thank you. - BSP offset ghost collisions
Important Information
We have placed cookies on your device to help make this website better. You can adjust your cookie settings, otherwise we'll assume you're okay to continue.