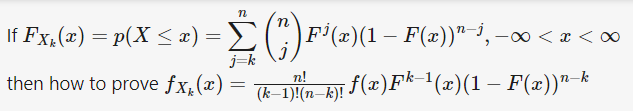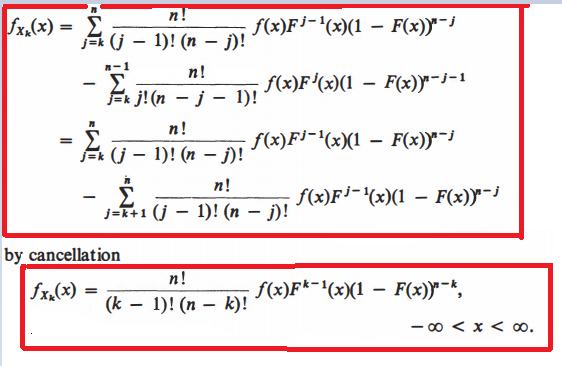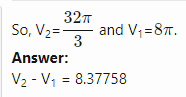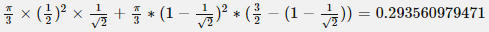Dhamnekar Win,odd

I got the answer to this question. I computed it as follows: [math]\displaystyle\int_0^{2\pi} 12 dt = 24\pi[/math]

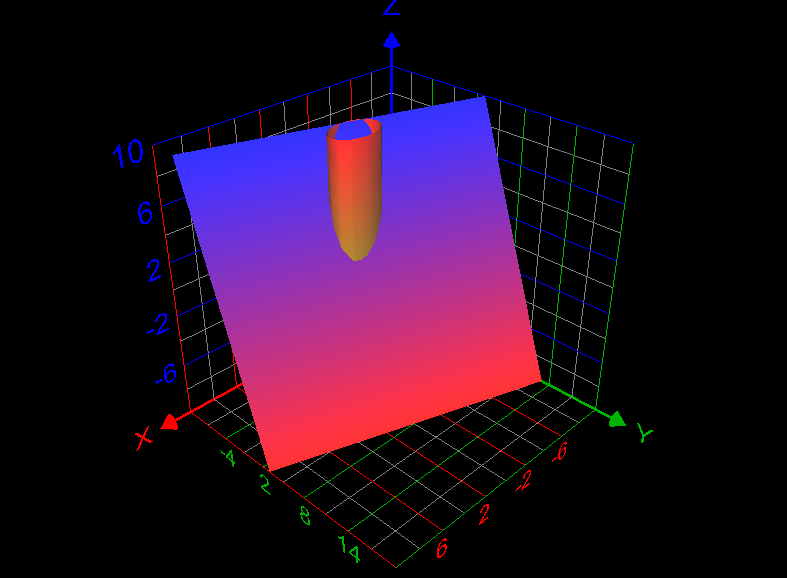
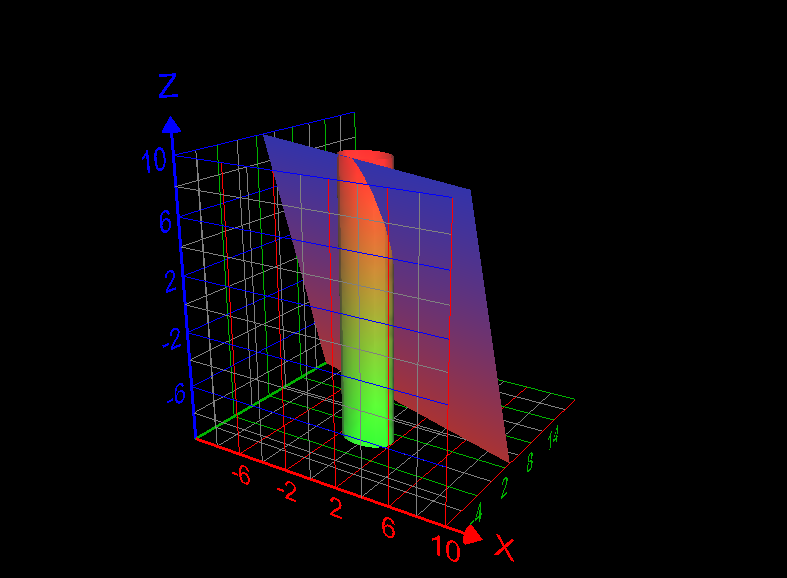
Use a line integral to find the lateral surface area of the part of the cylinder [math]x^2 +y^2 =4[/math] below the plane x + 2y + z =6 and above the xy-plane. How to answer this question? What is the answer of this question? Graph of the required lateral surface area of the cylinder is given below:

I tag this question as 'SOLVED'. Author's computations are correct. Thank you.

After studying these author's computations, I understood the differentiation part but I don't understand cancellation part and final term computation.

Author computed [math]F_{X_k} (x)[/math] as follows. but I don't understand it. Would any member explain me the following computations?

Answers to all of the aforesaid questions are affirmative.

I think my answer in the original post is incorrect. So, I want to correct it. My corrected answer is [math] \displaystyle\int_0^{2\pi}\displaystyle\int_0^2\displaystyle\int_0^4 r dz dr d\theta =16\pi [/math] Is this answer correct?

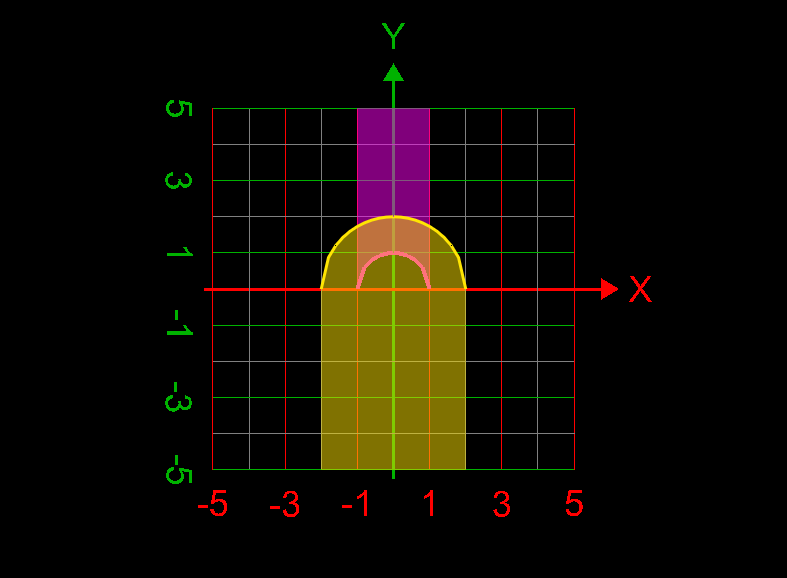
Find the volume of the solid bounded by [math]z = x^2 + y^2 [/math] and [math] z^2 = 4(x^2 + y^2) [/math] My attempt to answer this question: [math] \displaystyle\int_0^{2\pi}\displaystyle\int_0^2\displaystyle\int_0^4 1 \rho^2 \sin{(\phi)} d\rho d\phi d\theta = -\frac{128\pi \cos{(2)}- 128\pi}{3}= 189.822143919[/math] Is this answer correct?

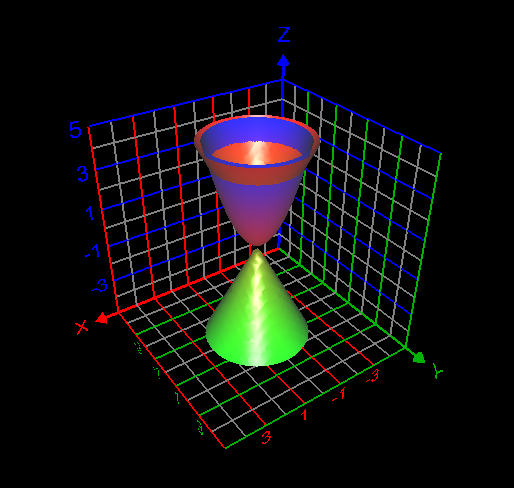
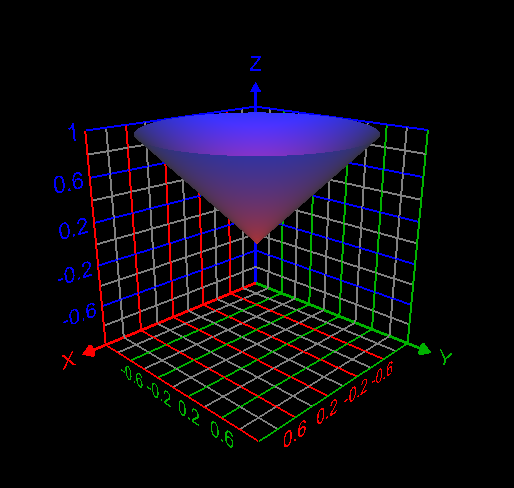
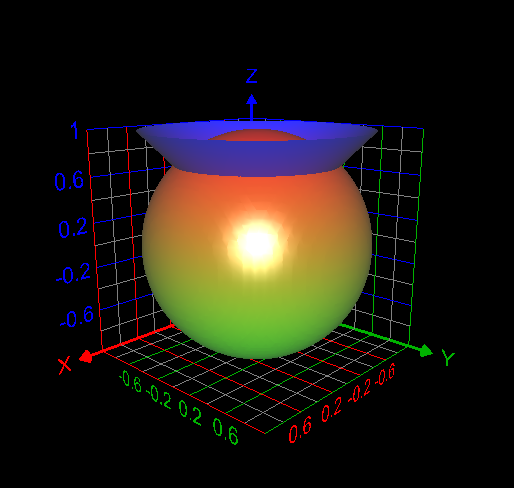
I computed the volume inside both the sphere [math] x^2 + y^2 + z^2 =1[/math] and cone [math] z= \sqrt{x^2 + y^2}[/math] as follows: [math]\displaystyle\int_0^{2\pi} \displaystyle\int_0^{\frac{\pi}{4}}\displaystyle\int_0^1 \rho^2 \sin{\phi}d\rho d\phi d\theta= 0.61343412301 =\frac{(2-\sqrt{2})\pi}{3}[/math]. This answer is correct.

I want to correct the volume asked in the question computed by me = [math] \frac{\pi}{3} \times \frac12 \times \frac{1}{\sqrt{2}} + \frac{\pi}{3} \times (1-\frac{1}{\sqrt{2}})^2 \times (\frac{3}{\sqrt{2}} -(1-\frac{1}{\sqrt{2}}))=0.534497630798[/math]

My attempt: I graphed the cone inside the sphere as in my first post. But I don't understand how to use the change of variables technique here to find the required volume. My answer without using integrals is volume of the cone + volume of the spherical cap = Is this answer correct? If correct, how to derive this answer using integration technique?

Find the volume V inside both the sphere x2 + y2 + z2 = 1 and the cone z = [math]\sqrt{x^2+ y^2}[/math] How to use change of variables technique in this problem?

Yes. From that point of view, this program is wrong. But we already decided to ignore the leap year and we mentioned that as the comment.

I tag this question "SOLVED". I got the correct answer.

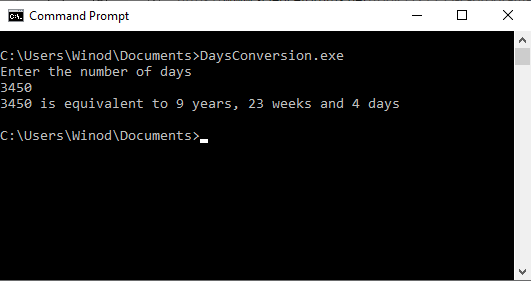
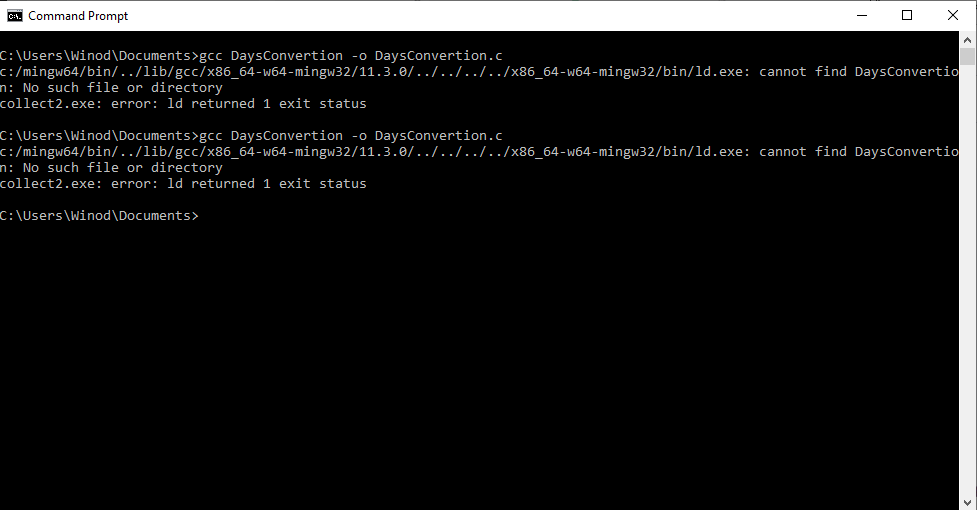
I have downloaded and installed ' C c-programs application from Windows store. I copied one program named 'Days Convertion' from it to my Notepad++ and saved it as c source file in the Documents folder. When I tried to compile it using gcc, gcc said unable to find the file. How can I fix this error? The c program is as follows: /* Write a c program to convert given number of days to a measure of time * given in years, weeks and days. For example 375 days is equal to 1 year * 1 week and 3 days (ignore leap year) */ #include stdio.h #define DAYSINWEEK 7 void main() { int ndays, year, week, days; printf("Enter the number of days\n"); scanf("%d",&ndays); year = ndays/365; week = (ndays % 365)/DAYSINWEEK; days = (ndays%365) % DAYSINWEEK; printf ("%d is equivalent to %d years, %d weeks and %d days\n", ndays, year, week, days); } /*----------------------------------------------- When I tried to compile it using gcc at windows command prompt, I got the following error several times. After giving this command at command prompt, 'DaysConvertion.c' file disappeared from the Documents folder. How can I fix this error?

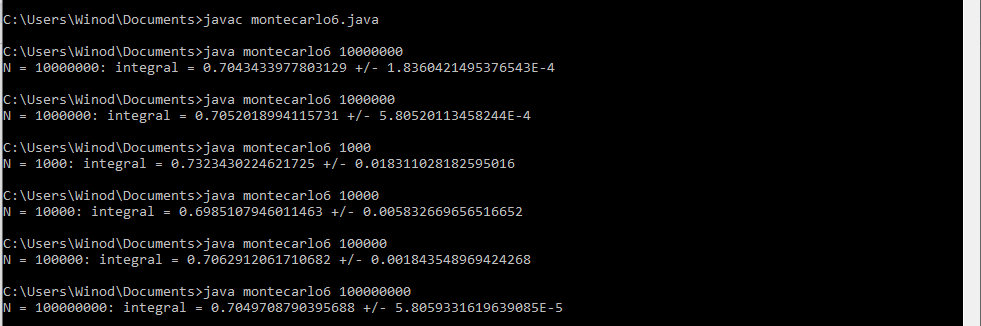
Yes. I think you are correct because as per your suggestion, I modified my Java program and I got the correct answer as given by author i-e 0.705. The modified java program and its new output is given below: //Program to approximate the double integral of f(x,y)=e^xy over the //region bounded by x=-1, x=1, y=0, and y=x^2 public class montecarlo6 { public static void main(String[] args) { //Get the number N of random points as a command-line parameter int N = Integer.parseInt(args[0]); double x = 0; //x-coordinate of a random point double y = 0; //y-coordinate of a random point double f = 0.0; //Value of f at a random point double mf = 0.0; //Mean of the values of f double mf2 = 0.0; //Mean of the values of f^2 for (int i=0;i<N;i++) { //Get the random coordinates x = 1 * Math.random() ; //x is between 1 and 0 y = 1 * Math.random() ; //y is between 0 and 1 if (y < Math.pow(x,2)) { //the point is in the region f = Math.exp(x*y); // Value of the function mf = mf + f; //Add to the sum of the f values mf2 = mf2 + f*f; //Add to the sum of the f^2 values } x = -1 * Math.random() ; //x is between -1 and 0 y = Math.random() ; //y is between 0 and 1 if (y < Math.pow(x,2)) { //the point is in the region f = Math.exp(x*y); // Value of the function mf = mf + f; //Add to the sum of the f values mf2 = mf2 + f*f; //Add to the sum of the f^2 values } } mf = mf/N; //Compute the mean of the f values mf2 = mf2/N; //Compute the mean of the f^2 values System.out.println("N = " + N + ": integral = " + vol()*mf + " +/- " + vol()*Math.sqrt((mf2 - Math.pow(mf,2))/N)); } //The volume of the rectangle [-1,1]x[0,1] public static double vol() { return 1*1; } } The new program's output:

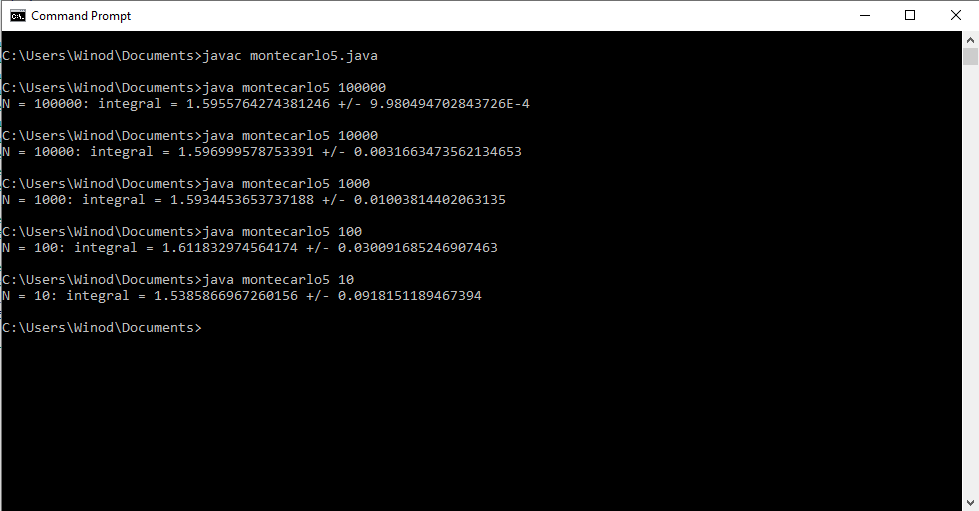
Write a program that uses the Monte Carlo method to approximate the double integral [math] \displaystyle\iint\limits_R e^{xy}dA [/math] where [math] R= [-1,1] \times [0, x^2][/math]. Show the program output for N = 10, 100, 1000, 10000, 100000 and 1000000 random points. My attempt: //Program to approximate the double integral of f(x,y)=e^xy over the //region bounded by x=-1, x=1, y=0, and y=x^2 public class montecarlo5 { public static void main(String[] args) { //Get the number N of random points as a command-line parameter int N = Integer.parseInt(args[0]); double x = 0; //x-coordinate of a random point double y = 0; //y-coordinate of a random point double f = 0.0; //Value of f at a random point double mf = 0.0; //Mean of the values of f double mf2 = 0.0; //Mean of the values of f^2 for (int i=0;i<N;i++) { //Get the random coordinates x = Math.random() ; //x is between 0 and 1 x = -1 * Math.random() ; //x is between -1 and 0 y = Math.random(); //y is between 0 and 1 f = Math.exp(x*y); // Value of the function mf = mf + f; //Add to the sum of the f values mf2 = mf2 + f*f; //Add to the sum of the f^2 values } mf = mf/N; //Compute the mean of the f values mf2 = mf2/N; //Compute the mean of the f^2 values System.out.println("N = " + N + ": integral = " + vol()*mf + " +/- " + vol()*Math.sqrt((mf2 - Math.pow(mf,2))/N)); } //The volume of the rectangle [-1,1]x[0,1] public static double vol() { return 2*1; } } Program Output is as follows: Correct integral =0.705; My Java program showed a integral 1.596 which is wrong, so my program is also wrong. How do I debug this program?

Are these above normality computations correct? If yes how? I don't understand these computations. Any chemistry help will be accepted.

Answer to question(d): Co3+ + V2+ → Co2+ + V3+ Defined redox couple is Co3+/Co2+ system [math] [Co^{2+}] = \frac{0.0050 mol}{0.200L} =0.025 M, [Co^{3+}]= \frac{0.010 mol}{0.200 L}=0.050 M, E_{sol}= E^{\circ}_{Co} -\frac{0.059}{n} \log{\frac{[Co^{2+}]}{[Co^{3+}]}} = 1.82 V - \frac{0.059}{1}\log{\frac{[0.025]}{[0.050]}} =1.84 V [/math]

If I write the balanced equation as 2VO2+ + Zn0 + 2H+ ⇌ 2VO2+ + Zn2+O-2 + H2O Is this correct?

Hi, Thanks for finding out the fault in my answer. Now, I rewrite the corrected balanced reaction 2VO2+ + Zn0 + 4H+ ⇌ 2VO2+ + Zn2+ + 2H2O