Dhamnekar Win,odd

1)In the titration of 0.010 M HNO3 (Nitric acid), the reaction equation is NaOH + HNO3 → NaNO3 + H2O. At the equivalence point, [NaNO3] = 0.005 M. At the equivalence point, equal volume of hydroxide solution have been added to the acid solution and all of the hydronium ions resulting from HNO3 have been converted to water. The solution at this point is simply an aqueous solution of sodium nitrate. Na+ + OH- + H3O+ + (NO3)- ⇌ 2H2O + Na+ + (NO3)-. Since neither sodium ions nor nitrate ions reacts with water, the solution is neither acidic nor basic; that is [H3O+] = [OH-] = 10-7 M. pH at the equivalence point is therefore 7.0 Indicator such as Phenol red (C19H14O5S) must be used which can respond to a pH of 7, the exact pH at the equivalence point. 2) In the titration of 0.010 M of ClCH2COOH (Chloroacetic acid), the reaction equation is ClCH2CO2- + H2O → ClCH2CO2H + OH- x = [OH-] = [ClCH2CO2H] ; 0.0050 - x = [ ClCH2COO-]; Kb = [math] \frac {x^2}{0.0050 - x}= \frac {K_w}{K_a}= \frac {10^{-14}}{1.4 \times 10^{-3}}= 7.1 \times 10 ^{-12} [/math] x= 1.9 × 10-7 M = [OH-]; pOH = -log(1.9 × 10-7 ) =6.72 ; pH =7.28. Indicator such as Phenol red (C19H14O5S) must be used which can respond to a pH of 7.28, the exact pH at the equivalence point. 3) In the titration of 0.010 M of O2NC6H4OH (o-nitrophenol), the reaction equation is O2NC6H4O- + H2O → O2NC6H4OH + OH-. x= [OH-] = [ O2NC6H4OH] and 0.0050 - x = [O2NC6H4O-]; Kb = [math] \frac{x^2}{0.0050 - x}= \frac{K_w}{K_a}= \frac{10^{-14}}{6.8 \times 10^{-8}} = 1.4 \times 10^{-7} [/math] x = 2.6 × 10-5 M ; pOH = -log (2.6 × 10-5 ) = 4.58; pH = 9.42 Indiactor such as Phenolphthalein must be used

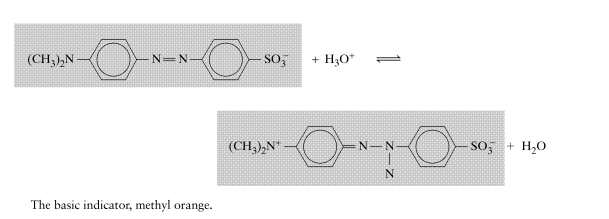
The following question is related to original question to some extent. Hence I am asking here.☺️ What is the explanation for the following acid-base behavior of Methyl Orange, an Indicator? I am working on the original question. Any Chemistry help will be accepted.

Please read 'Answer to question (b) assumes Maxwell-Boltzmann statistics. But how to show that the probability of each distinguishable distribution is [math] \frac {1} {n*N^r} [/math] ?' What is meaning of Note given?

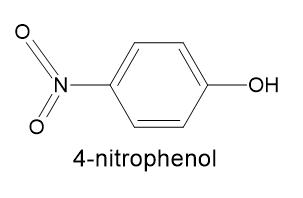
How to choose indiacator here for these above mentioned Acids titation? Is the below-given chemical compound structure of 4- nitrophenol same as given in the above question?

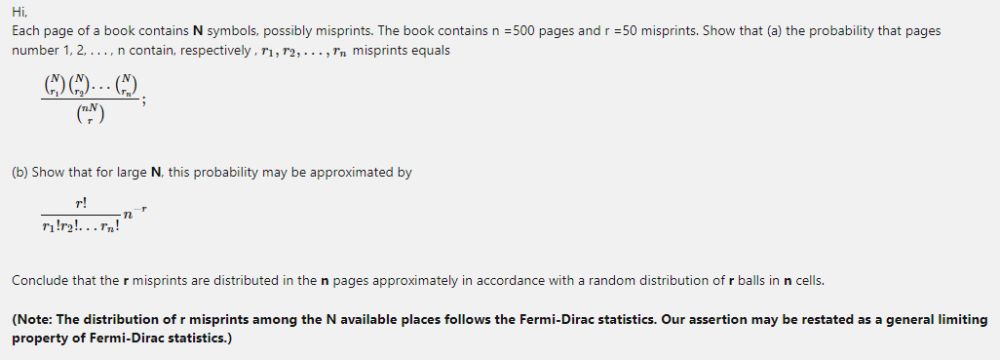
Answer to question (b) assumes Maxwell-Boltzmann statistics. But how to show that the probability of each distinguishable distribution is [math]n*(N)^r ?[/math] Why is Bose-Einstein statistics impossible here? Each distinguishable distribution have equal probability of [math]\frac{r!(n-1)!}{(n+r-1)!}[/math] under Bose-Einstein statistics.

This question is "SOLVED"

My attempt: I have following java program to solve similar equations using Newton's algorithm. What changes can be made to it to answer the above question? If below computer program is not useful, how to write the java program? I have netbeans (editor) for java programming.

I tag this question as 'SOLVED' as I got correct answers to all my questions. ☺️

pKa = -Log(ka), pH = pKa + log (NH3/(NH3 + NH4+)). So, Ka= 4.33504889257e-10 Now, [math]\frac{1}{10^{pK_a- pH}}=\frac{NH_3}{NH_3 + NH_4^+}=3.44345173426e-3[/math] Why 1 is added to denominator NH3 + NH4+? I think Emerson et al. developed the equation pKa = 0.09018 + 2729.92/T on experimental basis.

Rectified equation of f(fraction of NH3)= [math] \frac{1}{10^{(pKa-pH)} +1}[/math]

Please read here and the answer the following questions if you know: How did the author derive the following equations? pKa = 0.09018 + 2727.92/T f = 1/(10(pKa − pH) + 1) How would you interpret the answers given by 'R' using this package? How is NH3_mgL computed in 'R' using this package? What is the denomination of total ammonia in the argument given by the author in the examples ? Is it mol/L or in grams?

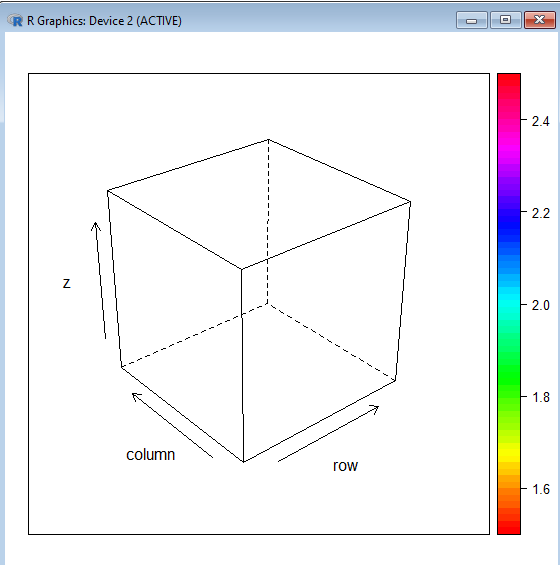
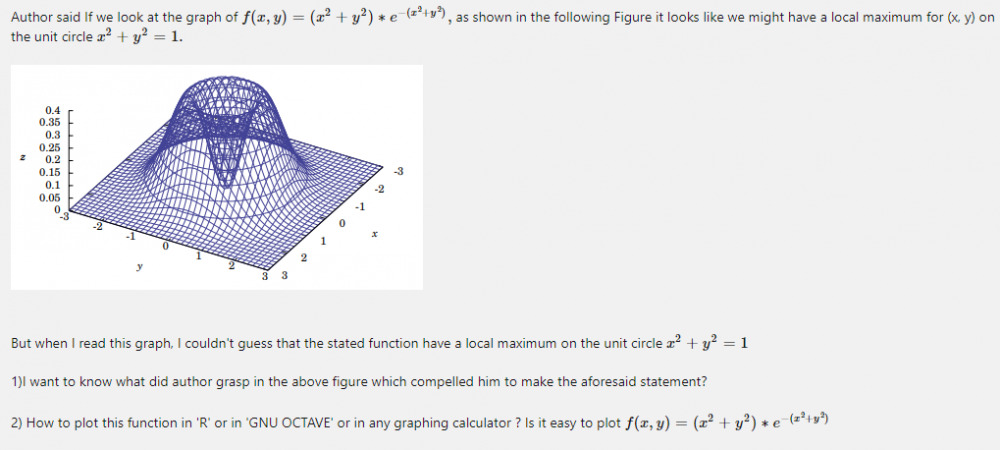
> fdejong <- function(x,y){return(x^2 +y^2)* exp(-(x^2+y^2))} > x<- seq(-1,1 , length=2) > y <- x > z <- outer (x,y, fdejong) > require(lattice) Loading required package: lattice > wireframe(z, drape=T, col.regions=rainbow(100)) What is this? I don't get it.😕🤔😧

More details about the question: The following theorem gives sufficient conditions for a critical point to be a local maximum or minimum of a smooth function (i.e. a function whose partial derivatives of all orders exist and are continuous). What are the changes, we must make in this theorem, in case f(x,y, z) and f(w, x , y, z)? How can we use the aforesaid rectified theorem to answer the following question? Find three positive numbers x, y, z whose sum is 10 such that [math] x^2 \cdot y^2 \cdot z[/math] is a maximum. My attempt : The critical point is x=4, y=4, z =2 How to compute D in this case?

Sufficient conditions for a critical point at (a, b, c) to be a local maximum or local minimum of a smooth function f(x, y, z).i-e [math]\nabla {f} (x,y,z)=0[/math]. How to define D in case of three variables namely x,y, z.

So, we will get the same first order correction for [math]1-\epsilon[/math] Isn't it? In which R package De Jong function is available ?

Hi,

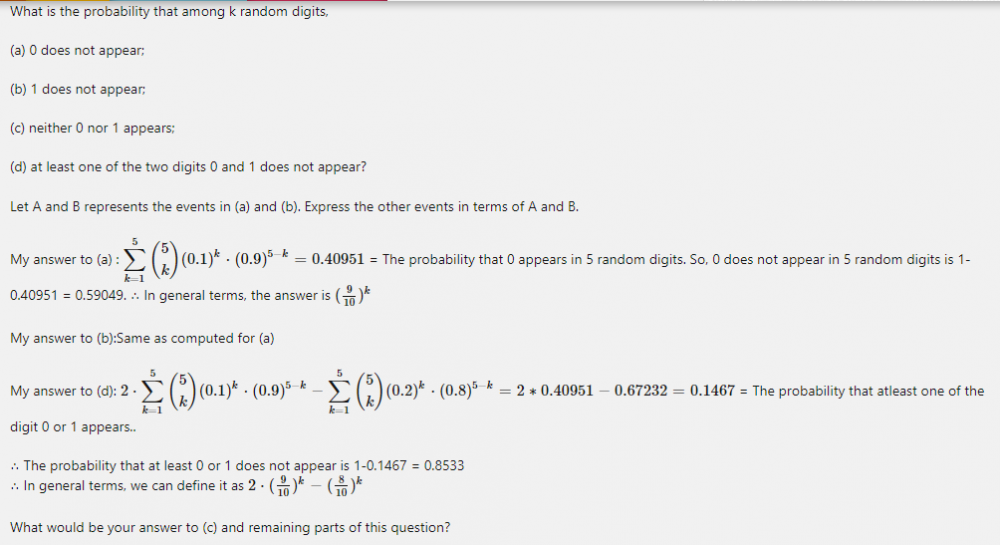
Rectified answer to (d): 2* (0.9)k - (0.81)k

Rectified answer to (c) if k =5 :[math]\displaystyle\sum_{k=1}^{5}\binom{5}{k} (02-0.01)^2 (0.81)^{5-k}= 0.6513215599 [/math]= The probability that either 0 or 1 appears. So, neither 0 nor 1 appears is 1-0.6513215599 = 0.3486784401 = (0.9)5 × (0.9)5 So, we can express event (c) in terms of A and B as A*B or P(A)* P(B). QED.

Answers to (a) and (b) are correct. [math](0.9)^5 \cdot (0.9)^5 = 0.3486784401 = (0.81)^5 [/math]whereas answer to (c) is (0.8)5 if k=5 So, there is minor difference of 0.1 in the probability in the answer to (c). I don't understand how did that arise?

All the digits 0-9

In hypergeometric distribution, n= population of n elements, r = sample size, n1 = elements recognized as having some defined criteria, n2 = n - n1 = remaining elements other than n1 . We seek the probability qk such that the sample size r contain exactly k recognized elements provided [math]k \geq 0, k \leq n_1 [/math] if n1 is smaller or [math] k \leq r[/math] if r is smaller. In such a case the probability [math]q_k =\frac{\binom{n_1}{k}\binom{n- n_1}{r - k}}{\binom{n}{r}} \tag {1}[/math] Now, I want to calculate n=8500, n1 =1000, r = 1000, k = 0 to 100. Inserting these values in (1), calculation of summation is very difficult. In such case, how can I use normal approximation to binomial distribution to find qk ? Do you have any clue or hint?

I am working on question (d) for answering it. Any chemistry help will be accepted. Do you know the correct answer for question(d)?

Whichever and whatever computations of Kc you use, eventually, final answer would be 0.17 mol /L SO2 should be added to the existing 0.2 mol/L SO2.

My corrected answer to (c) is [math] \frac{[1.6]^2}{[ 0.3 - 0.1 + x]^2 [0.20 - 0.05]}=125 \Rightarrow x = 0.17 [/math] mol SO2. ∴(0.17 mol SO2/L) (10 L)= 1.7 mol of SO2.