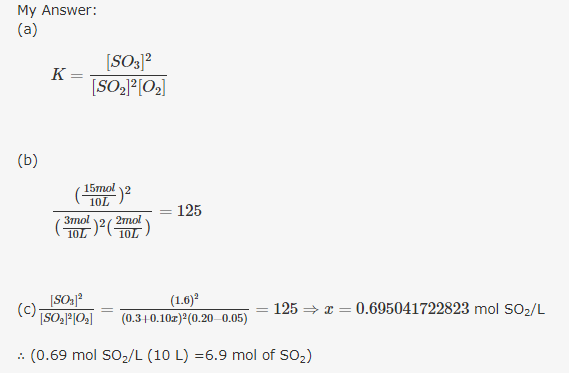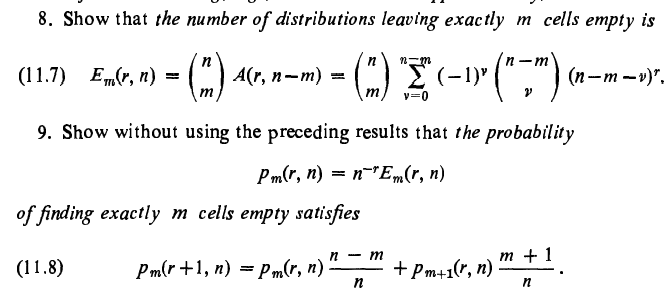Dhamnekar Win,odd

Please visit here

Yes, I forgot to square the concentration of SO3 in the numerator and the concentration of SO2 in the denominator of the fraction in (b). But R.H.S. 125 is correctly computed. But what is your opinion about my answer to (c)?

Are there any badges here for members?

Are these above answers correct? specifically last one (c)?

SOLVED

a) In how many parts, we can divide an infinite plane by n straight lines of which no two lines are parallel and no three lines are concurrent? b) In how many parts, we can divide an infinite space by n planes of which no four planes meets in a point and no two planes are parallel? How to answer both these questions? What are the answers to these questions? I am working on these questions. Any math help, problem solving hint will be accepted.

This problem is " SOLVED"

Thanks for your reply. I am working on the question 9 and statement in your reply to prove it practically as well as theoretically.

I know the answer to question 8. But how to answer question 9.

I tag this question as "SOLVED"

So, Eventually I did it. Using formula (1) we get [math] A(4,2)= \displaystyle\sum_{k=1}^{3}\binom{4}{k}\cdot \displaystyle\sum_{v=0}^{1}(-1)^v\cdot \binom{1}{v}\cdot (1-v)^{4-k}=14[/math] Using formula (1)we get[math] A(4,3)=\displaystyle\sum_{k=1}^{2}\binom{4}{k}\cdot\displaystyle\sum_{v=0}^{2}(-1)^v\cdot \binom{2}{v} \cdot (2-v)^{4-k}=36[/math] Using formula (2) we get [math]A(4,2)=\displaystyle\sum_{v=0}^{2}(-1)^v \cdot \binom{2}{v}\cdot (2-v)^{4}=14[/math] as expected Using formula (2) we get [math] A(4,3)=\displaystyle\sum_{v=0}^{3}(-1)^v\cdot \binom{3}{v}\cdot(3-v)^{4}=36 [/math] as expected. Thanks for your guidance.

But as per formula (2)r=4 and k=1 , which results in [math] (-1)^0 \cdot \binom{2}{0}\cdot(2-v)^3[/math] Formula (2) = [math]A(r-k,n) =\displaystyle\sum_{v=0}^{n}(-1)^v\binom{n}{v}(n-v)^{r-k}[/math]

So, for [math] k=1, A(3,2)=(-1)^0 \cdot \binom{2}{0} \cdot (2-v)^{4-1=3}[/math] Is this correct?

This answer refers to r=4 objects and n=2 cells question. We know A(r,n) =A(4,2)= 14 , My answer to A(r-k,n))=A(4-k, 2)=7 Is this answer correct?

[math]A(4-k,2)= (-1)^0 \cdot \binom{2}{0} \cdot(2-0)^{4-1} + (-1)^1\cdot \binom{2}{1} \cdot(2-1)^{4-2} = 8-1 =7[/math] Is this answer correct?

My attempt to derive general formula for A(r,n) =[math]\displaystyle\sum_{k=1}^{r-1}\binom{r-1}{k}\cdot A(r-k-1,n-1)[/math]

Author said to change order of summation and use binomial formula to express A(r, n+1) as the difference of two simple sums. So, I did it. As regards derivation of equation(1) using combinatorial arguments, author didn't write anything about that in his book. So, I don't know how to derive it.

If I put r=2, I get answer=3. If I put 4=3, I get answer=7. If I put r=4, I get answer=15. Now what is your suggestion?

I changed the order of summation and the expressed A(4,1+1=2)as the difference of two simple sums [math]\displaystyle\sum_{k=1}^{4}\binom{4}{k} \cdot\displaystyle\sum_{v=0}^{1}(-1)^v\cdot \binom{1}{v}\cdot(1-v)^{4-k}-\displaystyle\sum_{v=0}^{1}(-1)^v\cdot \binom{1}{v}\cdot(1-v)[/math] Now, what we can do?

That's what the author want to suggest. How can we change the order of summations in the answer which we got using formula (1) so that we get the answer 14?

Using formula (2), we get [math] A(4,2)= \displaystyle\sum_{v=0}^{2}(-1)^v\cdot \binom{2}{v}(2-v)^4=14[/math] Using formula (1), we get [math]A(4,2)=\displaystyle\sum_{k=1}^{4} \binom{4}{k}\cdot\displaystyle\sum_{v=0}^{1}(-1)^v \binom{1}{v}(1-v)^{4-k}=15[/math] Now, how can we remove the difference of one between these two answers?

I am trying to derive the formula (1) by combinatorial argument, but I didn't succeed. My difficulty to understand the Author's suggestions: 1) This is a classical occupancy problem. Assuming that all [math]n^r[/math] possible placements are equally probable, the probability to obtain the given occupancy numbers [math]r_1,...r_n[/math] equals [math] \frac{r!}{r_1! r_2!...r_n!} n^{-r}[/math] Here, we are concerned with only indistinguishable particles or objects. In Physics, this probability is known as Maxwell-Boltzmann statistics. Now, suppose, we have to put 4 objects in 2 cells. The number of distinguishable distributions of 4 identical objects into 2 cells is [math]\binom{3}{1}=3[/math].|***|*|, |*|***| or |**|**| But if we use formula (2) we get 14 as answer |**|**|, |**|**|, |**|**|, |**|**|, |**|**|, |**|**|, |***|*|,|***|*|,|***|*|, |***|*|, |*|***|, |*|***|, |*|***|, |*|***| . In case of A,B,C,D objects, we get |AB|CD|,|AC|BD|,|AD|BC|,|BC|AD|,|BD|AC|,|CD|AC|,|ABC|D|,|ACD|B|,|ABD|C|,|BCD|A|,|A|BCD|,|B|ACD|,|C|ABD|,|D|ABC| Using formula (1), we get [math]A(4,3)=\displaystyle\sum_{k=1}^{4}\binom{4}{k}*\displaystyle\sum_{v=0}^{2}(-1)^v*\binom{2}{v}*(2-v)^{4-k}=35[/math] I think this answer assumes distinguishable cells as well as objects. Now I don't understand , on what basis , we can say that this formula is derived assuming indistinguishable objects?

I did those computations for case(1) r=2, n=2 and case(2)r=2 and n=3. For case(1) The number of distinguishable distributions of 2 indistinguishable objects putting into 2 cells is 1 (equation or formula 1) and the numbers of distinguishable distributions of 2 distinguishable objects putting into 2 cells are 2(equation or formula 2) For case(2) The number of distinguishable distributions of 2 indistinguishable objects putting into 3 cells is -1 (equation or formula 1) and the number of distinguishable distributions of 2 distinguishable putting into 3 cells is 0(equation or formula 2) So, now how can we change the order of summation and use the binomial formula to express A(r, n+1) or in our case A(2,3) as the difference of two simple sums?

Assuming equation(2) to hold, how to express A(r-k, n) in equation (1) accordingly? How to change the order of summation and use the binomial formula to express A(r, n+1) as the difference of two simple sums as feller suggested? How to replace in the second sum v+1 by a new index of summation and use the following important property of binomial theorem [math]\binom{x}{r-1} + \binom{x}{r} = \binom{x+1}{r}[/math]?

The proof of the above formula was given in the book on probability by W.Feller