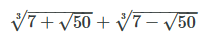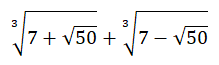-
Posts
5447 -
Joined
-
Days Won
53
Content Type
Profiles
Forums
Events
Everything posted by Genady
-
The questions, have been answered:
-
From past to future. Whose? What about it? I am not familiar with this terminology.
-

Having Trouble Answering the Question: "Why Do You Want to Work Here?"
Genady replied to Bunty12's topic in The Lounge
From my experience being on both sides of that table, the only reason to ask this question was to see what to expect, straight answer or bs. -

Having Trouble Answering the Question: "Why Do You Want to Work Here?"
Genady replied to Bunty12's topic in The Lounge
I don't understand (again). -

Having Trouble Answering the Question: "Why Do You Want to Work Here?"
Genady replied to Bunty12's topic in The Lounge
In which way? -

Having Trouble Answering the Question: "Why Do You Want to Work Here?"
Genady replied to Bunty12's topic in The Lounge
An honest answer was the only answer I was looking for when I was the interviewer. -
So? - I was not talking about solving. - I was not talking about "everything." - Math evolves.
-
You do not need to apologize because I have no idea what you are talking about.
-

Having Trouble Answering the Question: "Why Do You Want to Work Here?"
Genady replied to Bunty12's topic in The Lounge
You are applying for a job in a company, and you don't know why? -
I also think that because of the aforementioned conceptualization issues, mathematics is the only valid language to describe that.
-
I think that billions of neurons are just not enough and a brain with trillions or more neurons is required to conceptualize this.
-
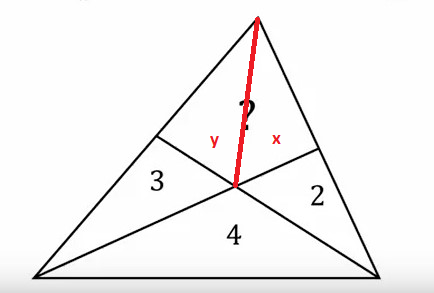
Like in the previous missing area puzzle (https://www.scienceforums.net/topic/131527-find-the-missing-area/?do=findComment&comment=1239116), it is helpful to switch to triangles: The area in question is x+y.
-
What are advantages of using Latex vs MS Word for math expressions in the posts? At least visually, IMO, the latter is better than the former. Compare Latex: MS Word: Plus, the latter gives more presentation choices such as font, size, etc.
-
Do they need to stay in the 3x3 configuration?
-
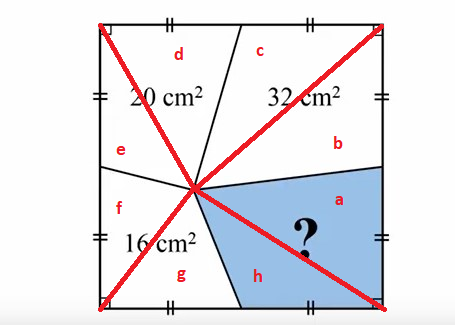
As we don't have much to do with areas of arbitrary shapes like these, but we know much about areas of triangles, let's make the triangles: The triangles above are named, a to h. The puzzle is, to find the area a+h.
-
Thank you for asking clarifying questions. There are no gridlines here, only the points, which are the intersection points of the 'imaginary' gridlines. The shape should not intersect any of these points. BTW, to be sure, the OP question has been changed to this: prove that any shape with area <1 can be placed on the plane without intersecting these points.
-
It doesn't let me see the whole step-by-step solution, but it looks like it just keeps simplifying the original expression. If so, it misses the beautiful insight: after the first step of taking the cube, the puzzle boils down to the simple equation, which is quickly solved by inspection.
-
What do you mean, it solves them right away?
-
So, after taking cube of the expression in question, and simplifying, we get it (i.e., the cube) being equal to Do you see something peculiar here?