-
Posts
5447 -
Joined
-
Days Won
53
Content Type
Profiles
Forums
Events
Everything posted by Genady
-
It is not a different topic because if it is moral then the answer to the OP question is yes.
-
What is immoral in the free market?
-
It depends on the culture, I guess. In my school, when we were given an equation to solve, there was always a possibility that the equation does not have a solution, in which case we were expected to prove that it is so. The idea of your proof is right and the proof is very close, except the issue you've mentioned about the area covered by the points. This issue can be eliminated by a modification of the proof where instead of removing points from a 1x1 square we find where to put a point. (I hope this last hint helps rather than distracts.) +1
-
The original goal has been inverted a few posts up. Now we try to prove this: Of course, it is either one or another, i.e., either there exists a shape that cannot be placed without touching or any shape can be placed without touching. But I have already hinted that the latter is correct.
-
Let me describe how I understand your construction. There is a list of numbered rows, one row for each natural number. Each row has a set of natural numbers, which contains natural numbers between 1 and the row number (including). Is this description correct? Putting it more formally: You construct a one-to-one (injective) map from set of natural numbers N to set of sets of natural numbers such that each n∈N is mapped to set R(n)= {x∈N | 1≤x≤n}. Correct?
-
The bot doesn't think so. I've asked a longer form of the question, with a hint: and got a more detailed answer: What??
-
A little algebra help for those who don't remember the formula: taking the cube of the expression in OP gives at first, Now, to simplify...
-
Et tu, Brute?
-
Well, that's too simple. But I did ask a simple question: Would you believe what its answer was?
-
Evidently.
-
No, you read way too much in this proof. It is quite a trivial one. It just shows that whatever set a row in your list has, is not a set of natural numbers. I don't see that digging into this proof will help to clear out the confusion. In fact, by now I don't know what the confusion is and thus don't know how to help with it. Maybe you can clearly state it from scratch.
-
OK, but imagine an arbitrary shape on a plane, an inkblot or even several inkblots (the shape doesn't have to be one connected piece) ...
-
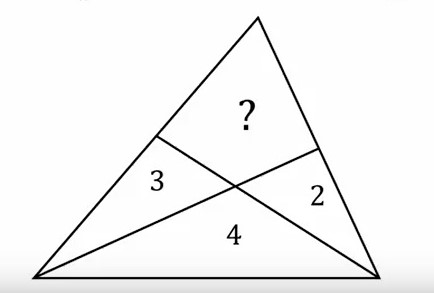
It is an arbitrary triangle with arbitrary lines in it. No other symmetries assumed. The three given areas uniquely determine the fourth area.
-
Think the other way around, invert the problem. Imagine a shape on a plane and look for a way to place the grid onto it without touching the shape.
-
I've asked the same question and got a longer and even more nonsensical response:
-
This does not seem to be a problem. I've asked, and the response was,