-
Posts
5723 -
Joined
-
Days Won
55
Content Type
Profiles
Forums
Events
Everything posted by Genady
-
I've noticed that the expressions for single Dirac field, chiral projection operators, and single complex scalar field have typos.
-

Does evolution have a direction?
Genady replied to PrimalMinister's topic in Evolution, Morphology and Exobiology
Yes. -

Does evolution have a direction?
Genady replied to PrimalMinister's topic in Evolution, Morphology and Exobiology
Yes, they have found another way. -

Does evolution have a direction?
Genady replied to PrimalMinister's topic in Evolution, Morphology and Exobiology
They get a lot from food. -
A capital letter has been cut from a sheet of paper and given a single fold: What letter is it? It could be, but is not an L.
-
Yes, in about 8 years. Nice, but would be more important for a younger person. This is a consideration. Maybe I should just buy batteries and keep them charged from the grid?
-
I wish. Maybe when I grow up... The glockenspiel is a good accompaniment to the song playing in my head.
-
OK! Do you want to try the same problem but with three bugs in the corners of equilateral triangle? Six bugs in the corners of equilateral hexagon? Just for practice
-
Learning to play (a simplified version of) it on my glockenspiel.
-
-
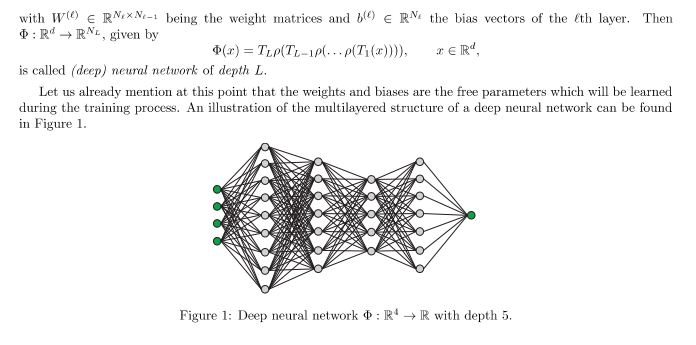
Only from reading technical literature and from playing with it online. I've retired before DNN was invented. Here is a basic description of its mathematical structure: At least that goal of AI has been achieved.
-
Yes, it is very easily confused.
-
IMO, it's just a run, calculation of the function for the question as an input. When the same question is asked again in the same session, its previous answer marked as 'not good' is added to the input, and the function is calculated again. And so on. If you start a new session and ask the same question, a different subset of the function is calculated for the same initial input as in the other session.
-
I don't think so. I think that it never calculates the full DNN function (too big), but rather each time a random subset of it.
-
It sounds as if one could calculate the movement of mass / energy, and then use it to calculate the spacetime geometry. But I don't think it is generally possible. The movement of mass / energy depends on the spacetime geometry, and one cannot calculate the former without the latter. I think that the equality between Einstein tensor and stress-energy tensor dictates the spacetime geometry, i.e., the spacetime geometry is dictated by the equation rather than by its parts. IOW, the spacetime geometry is such that it makes these two parts equal.
-
-
Correct. +1
-
This is an important reason. But it is somewhat reduced here, because about half of the electricity on the island is already produced by wind, and they plan to keep installing more turbines. Yes, it would be fun.
-
No, it is not.
-
I am receiving offers for solar panels and various configurations, with and without batteries. To make a decision I need to have a clear reason, why would I go for it. What are the possible reasons?
-
...should not you be on Kremlin by now.. ? They don't pay well enough.
-
Yes, to all three points above.