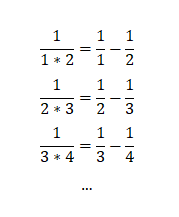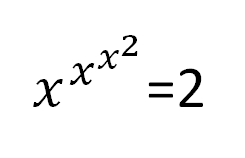Everything posted by Genady
-
How does ChatGPT work?
This does not seem to be a problem. I've asked, and the response was,
-
Confusion with finite sets vs an infinite set of natural numbers
It certainly did not. All is clear now, I hope.
-
Confusion with finite sets vs an infinite set of natural numbers
That is what that proof was about. If it is not relevant anymore, fine. The other question, has been answered, too. The answer is, yes.
-
Confusion with finite sets vs an infinite set of natural numbers
I mean the same that it means in math. I see that.
-
How does ChatGPT work?
Its answer is wrong. Try e.g. the triangle 3, 4, 5. Or 3.1, 4.1, 5.
-
How does ChatGPT work?
OK. If that is the meaning of his post, then fine. What made me doubt was that he didn't say "wrong answers" but rather "no answer". You always get some answer from ChatGPT, don't you?
-
How does ChatGPT work?
Does it have something to do with the OP?
-
Confusion with finite sets vs an infinite set of natural numbers
Well, it is not what it was saying. Rather, every natural number is listed, but the set of natural numbers is not.
-
A grid and a shape
Literally any shape. Should not touch / cover / contain any points of the grid. IOW, all parts of the shape are between the points of the grid = all points of the grid are outside of the shape. Any shape with a definite area is allowed. The only limitation is that its area is less than unity.
-
Confusion with finite sets vs an infinite set of natural numbers
Yes, this list has all natural numbers in it. It does not have a set of natural numbers in it. "Set of natural numbers" and "all natural numbers" are different entities.
-
Confusion with finite sets vs an infinite set of natural numbers
I don't know what you mean by the list being "complete." I didn't use this word.
-
Confusion with finite sets vs an infinite set of natural numbers
Here it is with a technical modification to fit your new list. We want to show that the set S = {x∈N | x≥1} is not in your list. Let's assume that the set S is in your list. Then there is a row, r, in the list with the set S. The row r has the set R = {x∈N | x=r} Evidently, R ≠ S which contradicts the assumption. Thus, S in not in the list.
-
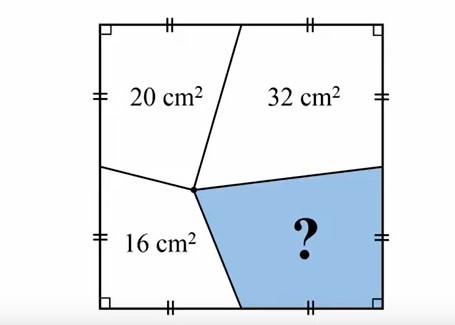
Find the missing area
- Confusion with finite sets vs an infinite set of natural numbers
Thank you. I didn't know this.- Confusion with finite sets vs an infinite set of natural numbers
So, the "RCL" in the text you've posted stands for the RCL as defined in this article. Is it correct?- Is a moral free market possible?
It is your opinion. I disagree, but this is not my point. My point is that, as this example shows, we do not "all know what's wrong..." At least one of us don't know here.- Is a moral free market possible?
Even if the man is Gaddafi, or Mussolini?- Confusion with finite sets vs an infinite set of natural numbers
One technical question here. The last paragraph refers to "RCL", but I didn't see it defined above, unlike the "RCF". What does the "RCL" stand for?- Spoiler is not hidden
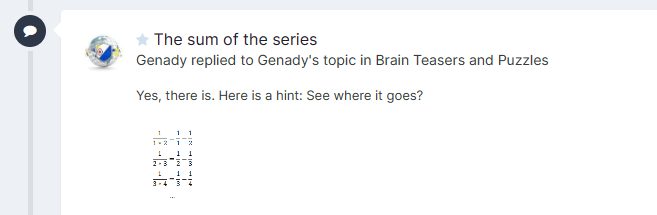
I've placed an image in hidden spoiler in my post. It is hidden there, but it is not hidden in the preview on activities list:- The sum of the series
- Multi story equation
- Confusion with finite sets vs an infinite set of natural numbers
Because the sets which appear on the rows in the new list are different from the old list.- Confusion with finite sets vs an infinite set of natural numbers
That proof has to be modified for the new list. When modified appropriately, it works just fine. I don't see a problem.- Confusion with finite sets vs an infinite set of natural numbers
Absolutely. I think that has been established some time ago, hasn't it? Why but? It doesn't contradict anything, does it?- Confusion with finite sets vs an infinite set of natural numbers
The answer is in this statement: This statement means that for every natural number there is a row in the list. That row, by construction, contains that number. Consequently, every natural number is present in some row in the list. - Confusion with finite sets vs an infinite set of natural numbers
Important Information
We have placed cookies on your device to help make this website better. You can adjust your cookie settings, otherwise we'll assume you're okay to continue.