Genady

Free entertainment. Even leaves one with a fuzzy feeling that they learned something.

Roadside Picnic - Wikipedia

As mentioned in the link given above, Since 1 Planck mass is approximately 21.76 micro-grams, I've posted this:

Sure. I thought rather that it is in micro-grams.

A few grams?

From my SCUBA diving days, I remember that argon was used for dry suit inflation in cold water diving because of its thermal insulation and non-corrosive properties as well as its low cost.

Yes. The time dilation does not happen at some event or events along the ship's worldline, but rather accumulates along the entire worldline. You can have a wild worldline with accelerations, decelerations, turning back and forth, etc., like this, for example: You divide that line into infinitesimal straight segment. On each segment, the proper time of the traveler is \[d \tau^2 = dt^2-dx^2\]. Then you integrate, \[\int{d \tau}\] to obtain the total time of the travel on the traveler's clock. Just a matter of calculation, see above.

It is wrong to assume that physical processes during acceleration are responsible for the time dilation. Time dilation is a geometrical rather than a physical effect. It is caused by the geometry of Minkowski spacetime. Let me describe the "twin's paradox" when nothing happens during an "acceleration". There is a clock located at 4 lh (light-hours) from Earth which is synchronized with the clock on Earth. Let's call this point in space, T. A ship moves with the speed 0.8c past the Earth. At the moment when a clock on the ship passes the clock on Earth, it is set to whatever is the time on Earth. Let's say, 10:00. The ship reaches the point T in 4/0.8=5 hours in the Earth time. The clock in T, which is synchronized with the clock on Earth, shows 10:00+5=15:00 when the clock on the ship passes it. However, the clock on the ship shows at this exact point in spacetime, i.e., as the two clocks are side-by-side, 10:00+3=13:00, because the time dilation factor for the speed of 0.8c is 0.6, and thus the trip to the point T takes 5*0.6=3 hours in the ship time. At the same exact point in spacetime, another ship passes the point T, going toward the Earth with the speed 0.8c. They grab the ship's clock and take it back to Earth. This trip back takes the same 5 hours in the Earth time and the same 3 hours in the ship time. So, when the clock returns to Earth, the clock on Earth shows 10:00+5+5=20:00, while the returned clock shows 10:00+3+3=16:00. Done.

This is how the "twins' paradox" is usually set up.

As you were writing that post, you were an accelerating observer, according to the equivalence principle. The ISS, for example, is a nonaccelerating one. Here are all your answers.

I think you can figure it out yourself. Hint: compare with tidal effects, which exist on Earth but not on an accelerating spacecraft.

Here is my intuition. Let's assume that I artificially narrow myself to the range [N, N]. I.e., my range contains only one integer. Does it lower my probability to win? No, it does not. The probability is still 1/N, like that of everyone else.

deleted

Hmmm... My blood is just dark green there. Not fluorescent at all.

This is factually incorrect. Observationally, the cosmic microwave background radiation is redshifted in one direction and blueshifted in the opposite direction. It is attributed to our peculiar motion relative to the cosmological comoving reference frame. Only after this peculiar motion is removed, the universe appears to expand isotropically.

I also am very far from being an expert, rather just a witness. In the case I've witnessed, specific environmental factor has made obvious a very serious form of schizophrenia, but then its signs could be traced back for years of misdiagnosis.

It depends on the symmetries of a situation. For example, a spherically symmetric case, e.g., Schwarzschild black hole, is usually visualized in 2D, i.e., temporal and radial.

Exactly. In the spacetime, they both have curvature of about 1 lightyear radius:

At the very far distance, the angle between light rays from the star becomes 0, that is the rays are just parallel to each other. Draw the picture and you will see what happens to the shadow when the rays are parallel.

1 metre, 2 metres, 10 metres, assuming the shadow is perpendicular to the light ray.

You are spoiling my question in the post right above yours ... 😉

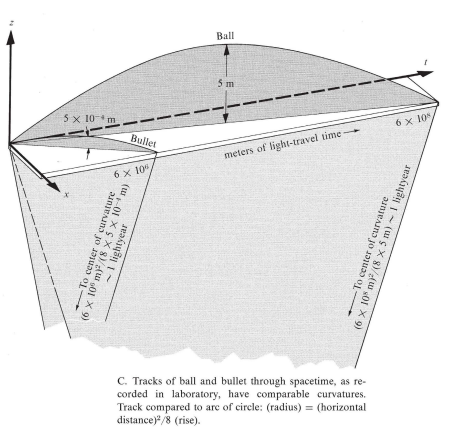
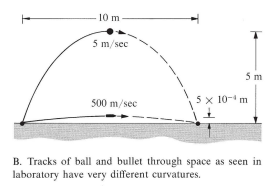
The main problem with the trampoline analogy is that it has nothing to do with the gravity related spacetime curvature. A curious student should ask after watching it, "How can the tracks of a ball and of a bullet be curved so differently if that curvature arises from the geometry of space?" (MTW, Gravitation (p. 32).)

No, I am not interested in this distinction. Sorry that what I said or how I said it sounded like this distinction is of any importance to me.

One might say whatever one wants.

This analogy doesn't work because a particle does not extend into its field in QFT, but rather it is its field when the latter is not in the ground state.