Genady

Well, thank you for letting me know. I'll take a note and will not waste my time anymore.

Here it is. R is where C receives the signal, and S is where B receives the signal:

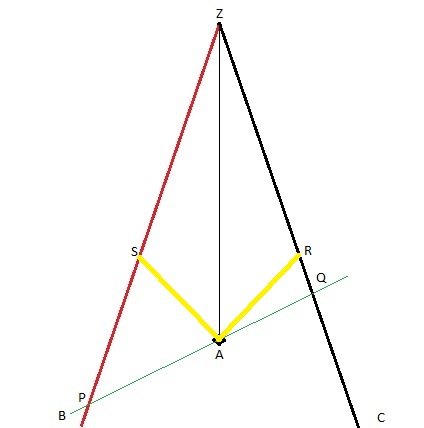
1) This is why the spacetime diagrams are so useful. You can draw it in one frame, which will appear orthogonal, and draw and analyze on the same diagram any other frame, which will appear tilted relative to the first. This allows for comparison between frames. 2) They are points simultaneous with the emission of the signals in point A, in frame B. There is a straightforward rule, how to find simultaneous points for any frame on the diagram. The points P, Q, and A are simultaneous in the frame B, and A is the emission. There is nothing about the reception, yet. Do you want me to show the reception points?

At this moment (in B frame), PA is a distance from B to A (in B frame), and QA is a distance from C to A (in B frame). In your notation, PA = dist_B(B,A) and QA = dist_B(A,C). You see on the diagram that PA and QA are not, and cannot be, equal.

In the frame B, the moment when the signals go off in A is simultaneous with spacetime events P and Q. P is where in the spacetime B is at this moment. Q is where in the spacetime C is at this moment. Again, this moment in the B's time. Questions? Thanks. Neither it is mine.

Yes, the drawing is how A would see the situation. But we do not calculate for A, just establish what symmetrical means. On the next step, we consider B. OK?

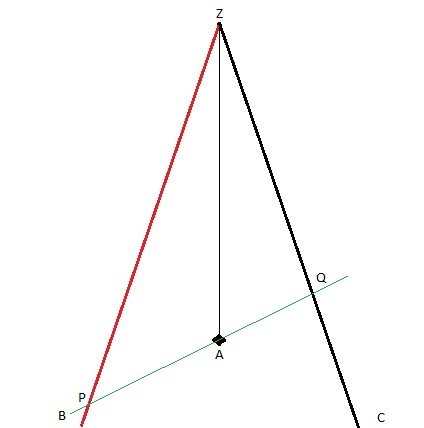
Here it is. Time axis goes up, position axis horizontal. I know we calculate for the B frame, but do you agree that this is how symmetrically travelling B and C would look in the frame of their meeting point? Point A is where the signals go off. Point Z is the meeting point. It is in the same position as A, but some time later, thus higher on the diagram. B comes toward the Z from the left, C comes toward Z from the right. They are always equally distanced from the meeting point. OK?

Every word by itself is clear. Their combination is not. Why do you want me to do the work? Just rephrase what you said.

It is not so in the B frame. I can show it to you on the spacetime diagram. Step-by-step, if you want. Should I show step 1? If yes, it will take me a few minutes to draw. If we agree on step 1, I'll draw step 2.

Then, whatever you said, you didn't say it clear enough and it was open to misinterpretation. Too many words - easy to misinterpret. Try to say it concisely. Math helps a lot in this. Frankly, I like to discuss science, not who said what.

No, no, I understand that. I am talking about the initial state, here: If these distances are equal in frame B in the initial state, then B and C are not travelling symmetrically between the source of the signal and their meeting point. If you want, I can show this on a symmetrical spacetime diagram. I think it is not possible to work with relativistic situations using a space diagram only. You need to show it on a spacetime diagram.

Yes, you did. You said, that if temperature does not change, then the work is done without heat transfer. This is not so. For example, in isothermal process, a work is done, the heat is transferred from the environment to the system, and the temperature does not change.

Here is a problem: If B and C are symmetrical relative to the signal in A, i.e, dist_A(B,A) = dist_A(A,C), then dist_B(B,A) ≠ dist_B(A,C). If, on the other hand, dist_B(B,A) = dist_B(A,C), then they are not symmetrical in A and thus their clocks don't need to be the same when they meet.

OK. The end point of both clocks is when they meet. What is a starting point of each?

I've noticed the edit: This confuses me even more regarding what you are calculating and what you expect in result. Velocity of C towards A relative to A? What about velocity of A towards B? I guess I will understand all this when I see your calculations.

Now I don't understand what you expect in the result. If A does not have any special properties, then the signal might go from B as well, i.e. A might be B itself. In this case, the signal goes off from B and B starts his clock, the signal gets received by C and C starts his clock, and sometime later they meet and compare their clocks? What is your prediction? Maybe I am confused because of the word "lectures" above (bold)? What do you mean?

So what? Heat is not conserved. Energy is conserved. The form of energy changes. There is no confusion there.

Given a choice between one's life and one's family well-being on one hand, and well-being of some foreign, perhaps bad, people on the other, most choose the former.

That is right. But the situation is described in A frame, specifically, B and C each move with speed v toward A, in the frame A. When you go to the frame B, what is the speed of C toward B? It is not 2v.

@Tom Booth, Here are examples of the textbook language as of 2021, as opposed to 1921, from Steven Weinberg, Foundations of Modern Physics, Cambridge University Press, 2021: In many places he uses the word 'heat', but it is always simply a short for the phrase 'heat energy'. Thus, to say that 'heat is destroyed' would be the same as saying that 'heat energy is destroyed', and this would be certainly wrong.

"2<3" means "2 is equivalent to <3"? No, it does not. For example, 1<3 as well, but 1 is not equivalent to 2.

@Tom Booth, In my sheet of paper analogy, the sheet of paper represents energy: - When the sheet is cylindrical, it is not flat. When the energy is in a form of work, it is not in a form of heat. Shape/form changes - not destroyed. - Being flat is not a constituent part of anything, it is a shape of the sheet. Heat is not a constituent part of anything, it is a form of energy.

In this case, the term "disappears" is used. Excuse me, but in my studies of thermodynamics, textbooks printed in 1921 were not employed. No. The energy is rolled up into a different shape. The heat was not a constituent part of the working fluid to start with.

This thread is about interpretations of the QM, not about other theories. If you want to discuss a theory which is different from QM, start another thread.

Electronic scales in a research lab. No, I did not. They were constantly in use by other researchers, too.