Genady

@kba, Thank you. I got the answer to my question:

bs

Oh, yes. Another long list. But this is technology, not science.

Yes, there are too many differences between English in science and out. Such comparisons should not be considered here. "Horizontal" differences are almost the same. How about wave-particle duality in QM? Historically, it was talked about quite a lot, but I don't think it is mentioned anymore. Not as an important concept anyway.

That does not count. They did not speak English then. 😉

Symmetry: from a simple geometrical meaning to invariance under transformation.

How about geometry? From a study of shapes and figures to a study of coordinate invariance.

Good examples above. Here is another: metal in chemistry vs metal in astrophysics (any element but hydrogen or helium).

This sounds like common vs scientific names of species in biology.

This is not a question in physics. Perhaps, in history of science. But not in physics.

As noted in another current thread, hundred years ago science textbooks used to talk about "destruction of heat". This language is not used in science today. I think, there might be many other examples of interesting evolution of scientific English, not involving changes in underlying physics. The first came to my mind, "mass". Not long ago (but after 1905) it often was used with a qualifier, e.g., "rest mass", "relativistic mass". Today, it is just "mass" meaning "rest mass", in all (almost?) textbooks, presentations, papers. Other interesting examples?

Copyright date does not necessarily invalidate the principle, but it often invalidates the verbiage. Language evolves, including the one used in science.

Well, thank you for letting me know. I'll take a note and will not waste my time anymore.

Here it is. R is where C receives the signal, and S is where B receives the signal:

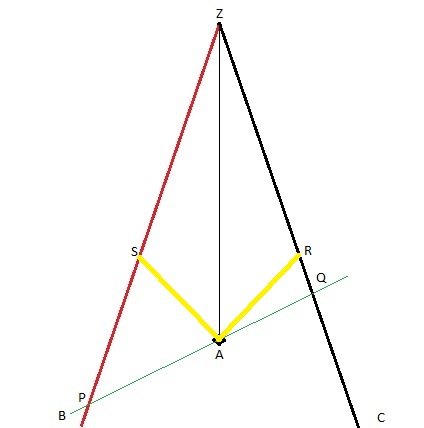
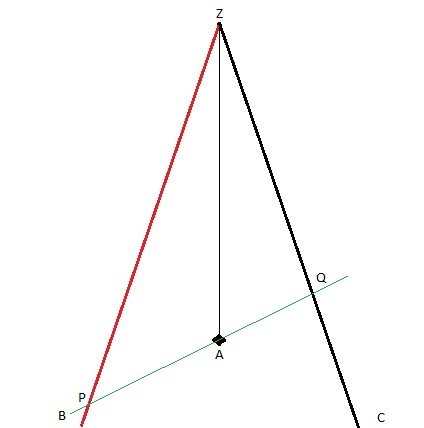
1) This is why the spacetime diagrams are so useful. You can draw it in one frame, which will appear orthogonal, and draw and analyze on the same diagram any other frame, which will appear tilted relative to the first. This allows for comparison between frames. 2) They are points simultaneous with the emission of the signals in point A, in frame B. There is a straightforward rule, how to find simultaneous points for any frame on the diagram. The points P, Q, and A are simultaneous in the frame B, and A is the emission. There is nothing about the reception, yet. Do you want me to show the reception points?

At this moment (in B frame), PA is a distance from B to A (in B frame), and QA is a distance from C to A (in B frame). In your notation, PA = dist_B(B,A) and QA = dist_B(A,C). You see on the diagram that PA and QA are not, and cannot be, equal.

In the frame B, the moment when the signals go off in A is simultaneous with spacetime events P and Q. P is where in the spacetime B is at this moment. Q is where in the spacetime C is at this moment. Again, this moment in the B's time. Questions? Thanks. Neither it is mine.

Yes, the drawing is how A would see the situation. But we do not calculate for A, just establish what symmetrical means. On the next step, we consider B. OK?

Here it is. Time axis goes up, position axis horizontal. I know we calculate for the B frame, but do you agree that this is how symmetrically travelling B and C would look in the frame of their meeting point? Point A is where the signals go off. Point Z is the meeting point. It is in the same position as A, but some time later, thus higher on the diagram. B comes toward the Z from the left, C comes toward Z from the right. They are always equally distanced from the meeting point. OK?

Every word by itself is clear. Their combination is not. Why do you want me to do the work? Just rephrase what you said.

It is not so in the B frame. I can show it to you on the spacetime diagram. Step-by-step, if you want. Should I show step 1? If yes, it will take me a few minutes to draw. If we agree on step 1, I'll draw step 2.

Then, whatever you said, you didn't say it clear enough and it was open to misinterpretation. Too many words - easy to misinterpret. Try to say it concisely. Math helps a lot in this. Frankly, I like to discuss science, not who said what.

No, no, I understand that. I am talking about the initial state, here: If these distances are equal in frame B in the initial state, then B and C are not travelling symmetrically between the source of the signal and their meeting point. If you want, I can show this on a symmetrical spacetime diagram. I think it is not possible to work with relativistic situations using a space diagram only. You need to show it on a spacetime diagram.

Yes, you did. You said, that if temperature does not change, then the work is done without heat transfer. This is not so. For example, in isothermal process, a work is done, the heat is transferred from the environment to the system, and the temperature does not change.

Here is a problem: If B and C are symmetrical relative to the signal in A, i.e, dist_A(B,A) = dist_A(A,C), then dist_B(B,A) ≠ dist_B(A,C). If, on the other hand, dist_B(B,A) = dist_B(A,C), then they are not symmetrical in A and thus their clocks don't need to be the same when they meet.