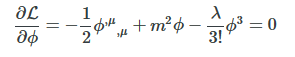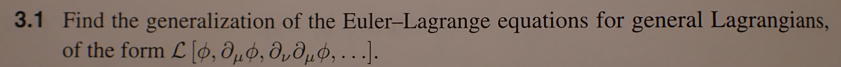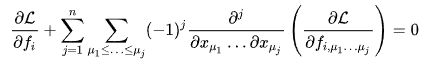Genady

1 and 2 (they are different expressions of the same, but 2 is more precise.) You have to do it because what happens at your location at that time. I.e., the spacetime geometry at that spacetime event.

All solutions obey this equation. The mass is not at the same location where the Schwarzschild metric is. I don't see why it would matter. There are simply more independent variables in the curvature tensor than there are independent equations in the Einstein field equation.

Aren't there many examples, at least in principle? In particular: "Q: The information that gets lost when we go from the Riemann tensor to the Ricci tensor does not affect the energy-momentum tensor nor Einstein’s equations. What is the meaning of this lost information then? A: It means that for a given source configuration, there can be many solutions to Einstein’s equations. They all have the same right-hand side, namely \(T^{\mu \nu}\). But they simply have different physical properties. For example, the simplest case is to ask: what if this energy-momentum stuff is zero? If it is zero, does it mean that there is no gravitation, no interesting geometry at all? No. It allows gravitational waves." Susskind, Cabannes. General Relativity: The Theoretical Minimum. Not according to this: homework and exercises - Non-zero components of the Riemann tensor for the Schwarzschild metric - Physics Stack Exchange

In the Einstein field equation, the curvature on one side and the energy-momentum on the other side are not lightlike separated. It is not local, contrary to

Thank you for the correction. I should've said, "... are not timelike or lightlike separated ..."

I see. It gets worse. Now, it is boring. Regurgitating of age-old philosophies. Hundreds or thousands of years old. In the recent decades, marketed by Deepak Chopra. I am out.

Not necessarily. For example, the Schwarzschild geometry exists in vacuum.

Sorry, I guess it makes sense to you, but it doesn't make sense to me. Just words. Got a model?

Yes, it has not. Every spacetime has a curvature.

Just replace "non-physical" with "physical" and "mind" with "brain": Science (as concept) is physical. Without this physical brain you could not read these words here on the page or any other book for that matter. Take the physical brain away from the world, and science ceases to exist. Yes.

Since energy-momentum and curvature are not timelike separated, there is no meaningful causal relation between them.

I did, and my answer was that \(\mathcal L\) is invariant under translation.

No.

The Lagrangian, \[\mathcal L(x)= \frac 1 2 \partial^{\mu} \phi (x) \partial_{\mu} \phi (x) - \frac 1 2 m^2 \phi (x)^2\] for a scalar field \(\phi (x)\) is said to be "Lorentz invariant and transforms covariantly under translation." What does it mean that it transforms covariantly under translation?

You also need the length of the pellet.

Isn't it rather 6000? 😄

Another ecological effect will be on organisms which use Moon for timing, for example, coral spawning.

It will stop slowing down (almost).

This ^^^^, I understand. This ^^^^, is only a distraction to me. (But generally, more often than not, I dislike analogies. Perhaps something individual.)

Yes, it is, in this sense: "This is extremely general. In any kind of gravitational field, as long as it is more or less constant with time, and not doing anything too radically relativistic, the coefficient in front of \(dt^2\) in the metric is always one plus twice the gravitational potential." Susskind, Cabannes. General Relativity: The Theoretical Minimum (p. 155).

I'm at ease with the Schwartz's notation by now. It is as simple as mentally substituting \(A_{\mu} g^{\mu \alpha} B_{\alpha}\) every time he writes \(A_{\mu} B_{\mu}\).

I'm looking where exactly, during a construction of the Feynman propagator \(D_F(x_1,x_2)\), a particle goes off-shell. It is on-shell all the way until before the last step: \(D_F(x_1,x_2)=\frac i {(2 \pi)^4}\int d^3 k \int d \omega \, e^{-i \vec k (\vec x_1 - \vec x_2)} \frac 1 {\omega^2 - \omega_k^2 + i \epsilon} e^{i \omega (t_1-t_2)}\) The particle is on-shell here because its 4-momentum is \((\omega_k, \vec k) \), where \(\omega_k^2 = \vec k^2+m^2\). Integration variable of the first integral is 3-momentum \(\vec k\), where each one of the three component varies from \(- \infty\) to \(\infty\). Integration variable of the second integral is energy \(\omega\), which also varies from \(- \infty\) to \(\infty\). Now, we combine these integration variables into a new 4-vector \(k=(\omega,\vec k)\), where each component varies independently from \(- \infty\) to \(\infty\). This 4-vector is not a 4-momentum of anything and thus is off-shell for a simple reason that there is no shell for it to be on. It is just an integration variable: \(D_F(x_1,x_2)=\frac i {(2 \pi)^4}\int d^4 k \, e^{-i \vec k (\vec x_1 - \vec x_2)} \frac 1 {\omega^2 - \omega_k^2 + i \epsilon} e^{i \omega (t_1-t_2)} = \frac i {(2 \pi)^4}\int d^4 k \frac {e^{k (x_1 - x_2)}} {\omega^2 - \omega_k^2 + i \epsilon}\) Being a generic 4-vector, \(k\) satisfies \(\omega^2=k^2+ \vec k^2\). Being an on-shell 4-momentum, \((\omega_k, \vec k) \) satisfies \(\omega_k^2 = \vec k^2+m^2\). Substituting these above, we get the final form of the Feynman propagator: \(D_F(x_1,x_2)= \frac i {(2 \pi)^4}\int d^4 k \frac {e^{k (x_1 - x_2)}} {k^2 - m^2 + i \epsilon}\) The particle, which is on-shell, is not explicit in this form. Instead, we have a generic variable \(k\), which is a Lorentz invariant way to package the four integration variables, and which is not a 4-momentum of any particle. Evidently, there are no off-shell particles here.

Unfortunately, I can't read this post: and I don't know how his result is different from mine, but it seems that his EL equation is the same as mine, <<<<< which is different from <<<<<<< I disagree with the latter. We need to use the generalized EL equation, which I have already derived in this exercise: and got the answer compatible with this: (Euler–Lagrange equation - Wikipedia)

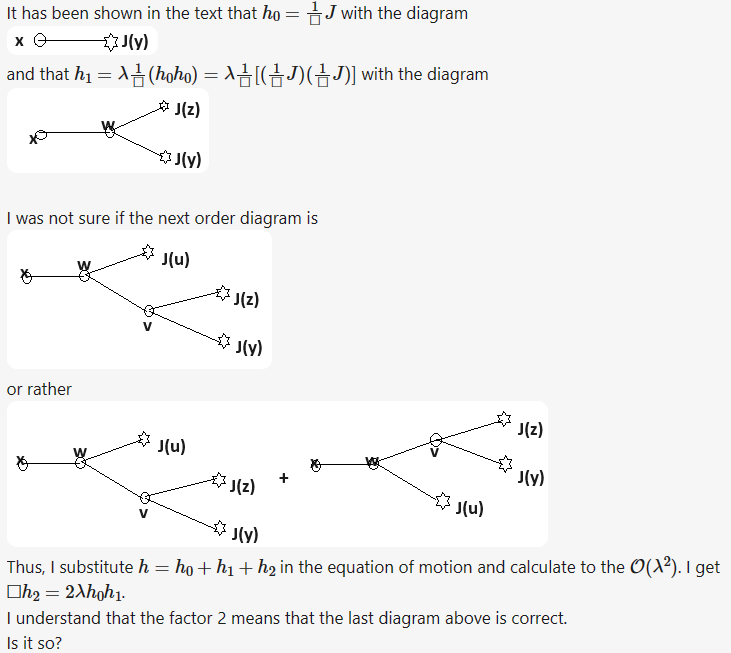
Write down the next-order diagrams for the equation of motion \(\Box h - \lambda h^2 -J =0\). Check the answer using Green's function method.

Q: How many constants \(c\) are there so that \(\phi(x)=c\) is a solution to the equation of motion? A: Three. \(c=0\) and two solutions for \(c^2= \frac {3!} {\lambda} m^2\) Q: Which solution has the lowest energy (the ground state)? A: The potential energy from the Lagrangian is \[\frac {\lambda} {4!} \phi^4 - \frac 1 2 m^2 \phi^2\]It is the lowest for the non-zero \(c\): \(- \frac{3!m^4} {4 \lambda}\).