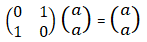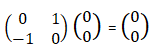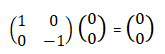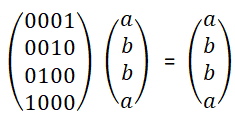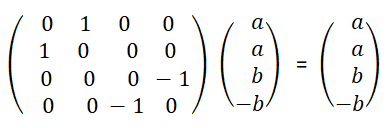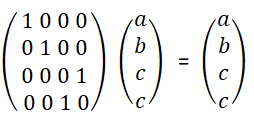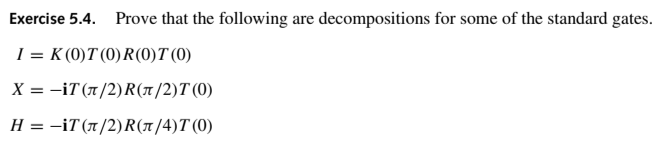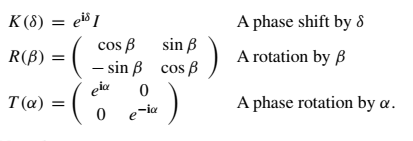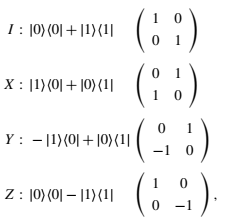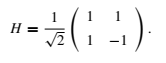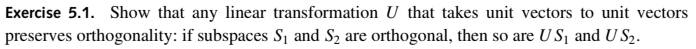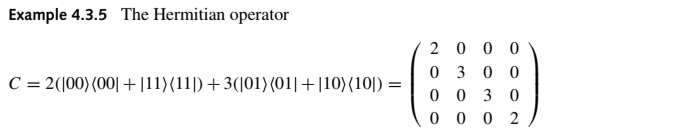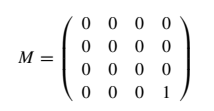Genady

Yes, you're right. Perhaps, interaction with a system in a mixed state would've been a correct answer?

Sure. Also look for decoherence.

Entanglement with a system in a mixed state.

F. (Academic grading in the United States - Wikipedia)

The algebra is wrong.

Here you are: (Color charge - Wikipedia)

Perhaps this short video, https://upload.wikimedia.org/wikipedia/commons/transcoded/7/72/Journey_of_Sound_to_the_Brain.ogv/Journey_of_Sound_to_the_Brain.ogv.720p.vp9.webm in the Ear - Wikipedia answers your question. (Although I don't understand the first sentence in the OP.)

No, they cannot because of relativity of simultaneity.

Whose brain?

The OP is not genuine. It is plagiarized from https://www.physicsforums.com/threads/height-of-a-stable-droplet-on-a-perfectly-wetting-surface.1057037/post-6964327.

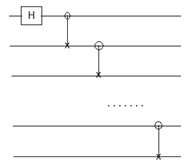
An n-qubit cat state is the state 1/√2 (|00 . . . 0〉 + |11 . . . 1〉). Design a circuit that, upon input of |00 . . . 0〉, constructs a cat state. ======== My idea is first to transform the first qubit to the superposition using the Hadamard gate and then to propagate the result to the rest of the qubits with the Cnot gates:

a. b. c. d. e. f.

For the reference: K(0) = T(0) = R(0) = I. Thus, K(0)T(0)R(0)T(0) = I. T(π/2) = i * 1 0 0 -1 R(π/2) = 0 1 -1 0 T(π/2)R(π/2)T(0) = iX. X = -iT(π/2)R(π/2)T(0). R(π/4) = 1/√2* 1 1 -1 1 T(π/2)R(π/4)T(0) = iH. H = -iT(π/2)R(π/4)T(0).

(From The New Yorker of October 23)

(For the reference, the BB84 is described here: https://www.scienceforums.net/topic/132653-quantum-key-distribution/) I assume that Eve always measures her qubit in the standard basis. Let's see what happens: 1. Alice's bit is 0. 1.1. Alice and Bob pick the standard basis. She sends |0〉. Eve applies Cnot: |0〉|0〉 ↦ |0〉|0〉. Bob gets 0. Correct. Eve gets 0. Correct. 1.2. Alice and Bob pick the Hadamard basis. Alise sends 1/√2(|0〉+|1〉). Eve applies Cnot: 1/√2(|0〉+|1〉)|0〉 ↦ 1/√2(|0〉|0〉+|1〉|1〉). 1.2.1. Bob gets 0. Correct. Eve gets 0. Correct. 1.2.2. Bob gets 0. Correct. Eve gets 1. Error. 1.2.3. Bob gets 1. Error. Eve gets 0. Correct. 1.2.4. Bob gets 1. Error. Eve gets 1. Error. 2. Alice's bit is 1. 2.1. Alice and Bob pick the standard basis. She sends |1〉. Eve applies Cnot: |1〉|0〉 ↦ |1〉|1〉. Bob gets 1. Correct. Eve gets 1. Correct. 2.2. Alice and Bob pick the Hadamard basis. Alise sends 1/√2(|0〉-|1〉). Eve applies Cnot: 1/√2(|0〉-|1〉)|0〉 ↦ 1/√2(|0〉|0〉-|1〉|1〉). 2.2.1. Bob gets 0. Error. Eve gets 0. Error. 1.2.2. Bob gets 0. Error. Eve gets 1. Correct. 1.2.3. Bob gets 1. Correct. Eve gets 0. Error. 1.2.4. Bob gets 1. Correct. Eve gets 1. Correct. Looks like Eve gets 75% of Alice's bits correctly and introduces 25% errors in the bits measured by Bob, the same as in the original scheme. Am I missing something?

My guess is that it is a result of evolution by sexual selection. Akin displays some birds make to attract mates.

I've made errors in the 'diagonal' part of the construction for the question 'd' above. One needs to be careful not to include diagonal terms in rows or columns which already have terms in them. Thus, the correction: /* diagonal */ |0+ 0-〉 〈0+ 0-| + |0+ 1+〉 〈0+ 1+| + |0+ 1-〉 〈0+ 1-| + |0- 1+〉 〈0- 1+| + |0- 1-〉 〈0- 1-| + |1+ 0-〉 〈1+ 0-| + |1- 0-〉 〈1- 0-| + |1+ 1-〉 〈1+ 1-| + |1- 1+〉 〈1- 1+|

They have eaten insects, too... And other not-so-attractive stuff.

Exactly. They indicate that there are no fruits there yet. So, for now, one should look for fruits somewhere else. Flowers should've been rather discouraging then.

Continuing exercise 5.2 above. d. Construct the operator as follows: U = /* required cloning */ |0+ 0+〉 〈0+ 0+| + |0- 0-〉 〈0- 0+| + |1+ 1+〉 〈1+ 0+| + |1- 1-〉 〈1- 0+| + /* transpose */ |0- 0+〉 〈0- 0-| + |1+ 0+〉 〈1+ 1+| + |1- 0+〉 〈1- 1-| + /* diagonal */ |0+ 0-〉 〈0+ 0-| + |0- 0+〉 〈0- 0+| + |0- 0-〉 〈0- 0-| + |0+ 1+〉 〈0+ 1+| + |0+ 1-〉 〈0+ 1-| + |0- 1+〉 〈0- 1+| + |0- 1-〉 〈0- 1-| + |1+ 0+〉 〈1+ 0+| + |1+ 0-〉 〈1+ 0-| + |1- 0+〉 〈1- 0+| + |1- 0-〉 〈1- 0-| + |1+ 1+〉 〈1+ 1+| + |1+ 1-〉 〈1+ 1-| + |1- 1+〉 〈1- 1+| + |1- 1-〉 〈1- 1-| e. This set includes c, thus impossible to clone.

It is obvious why bees and butterflies are attracted to flowers. But why do humans find flowers attractive?

a. U = 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 b. Same as a but in the {|+〉, |-〉} basis. c. If such U existed, it would transform U(|00〉) = |00〉 and U(|10〉) = |11〉. Then U(|+〉|0〉) = U(1/√2 (|0〉 + |1〉)|0〉) = 1/√2 (|00〉 + |11〉) ≠ |++〉, i.e. |+〉 would not be cloned.

(From: Rieffel, Eleanor G.; Polak, Wolfgang H.. Quantum Computing: A Gentle Introduction.) Take v in S1 and w in S2: 〈v|w〉 = 0. 〈Uv|Uw〉 = 〈v|U†U|w〉 = 〈v|w〉 = 0. Too easy.

Continuing exercise 4.21 above: c. Generally, if a measurement of the first qubit is H1 = a b c d and a measurement of the second qubit is H2 = x y z v then the measurement of the two-qubit system would be H = H1 ⊗ H2 = ax ay bx by az av bz bv cx cy dx dy cz cv dz dv The reference: The measurement A cannot be achieved by two single qubit measurements, because for ax = 0 either av = 0 or dx = 0, but in A, av = 1 and dx = 2. The reference: H1 = 1 0 0 π H2 = I The reference: The measurement C cannot be achieved by two single qubit measurements, because for ax = 2, av = 3, dx = 3, dv = 2 the ratio a/d = 2/3 and a/d = 3/2. The reference: H1 = H2 = 0 0 0 1

Yes, there are gravitational "grooves" which free falling objects follow. But these "grooves" exist in spacetime rather than in space. They are called, geodesics.