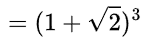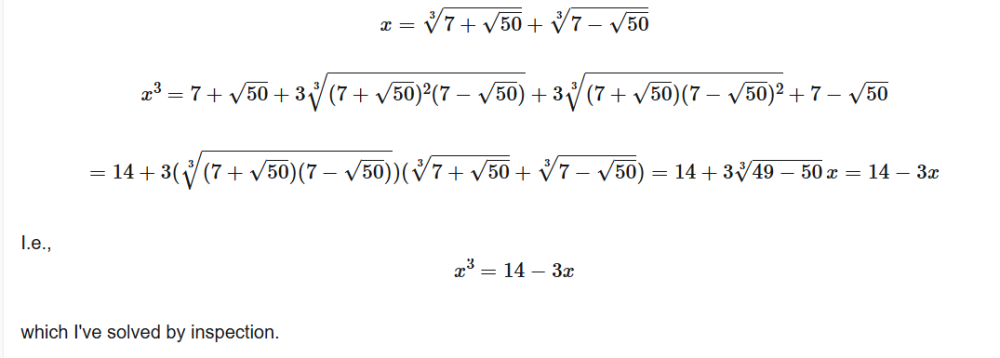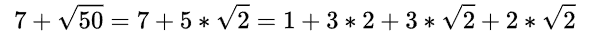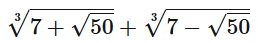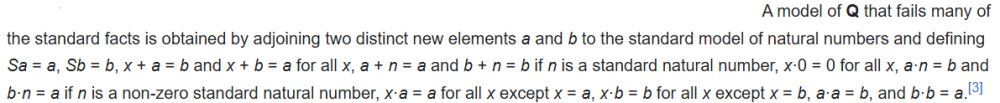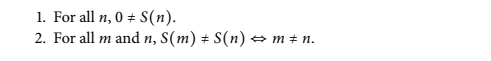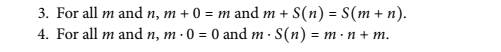Genady

Thank you!

Yes, it does. Here is the next step (attach this to the previous chain of equalities): Yes, I see what you mean. BTW, would you please remind me of the tags/delimiters for inserting LaTeX in SFn?

This is the same as how I've solved it: So, x=2. Then, somebody has showed me different way. I'll give you a hint: (I make these LaTeX expressions outside because I don't remember what the tags in SFN are.) However, these are not solutions.

If it is, this will be a third way 😉.

Yep, that's the only way I know. How about the one above it?

And another one, the last one of this kind that I seem to remember: Find two 4-digit numbers that multiply to give 4^8 + 6^8 + 9^8.

Here is another puzzle from the "Without a Calculator" set: I know of two different ways to solve it and I'm curious about your way.

This is correct.

Yes, 216 is specially related to the other numbers in the puzzle.

I got this nice little math puzzle elsewhere. I got it with a hint but try without the hint first. Here it goes: P.S. Without a calculator, of course.

'Oh, you aren't even ripe yet! I don't need any sour grapes.'

It appears to be quite simple:

I got the answer - Robinson arithmetic - Wikipedia.

Yes, the galactic North Pole and our North Pole do not coincide, but this doesn't change the sense of rotation. Important fact is that the galactic North Pole lies in our northern hemisphere. AFAIK, our galaxy rotates clockwise as viewed from the galactic North Pole. This is what I remember from my astronomy class years ago.

It doesn't sound right. Anyway, here is how it looks:

Stillwell's "Reverse Mathematics" says on p.41, Unfortunately, there is no example of such model. Does anybody know such? For the reference, here are the axioms 1-4:

"Ah, look at all the lonely people"

We have exactly such system where I live. Hospital nurses visit daily elderly living alone.

Clockwise when observed from the North.

I thought that Klein-Gordon's describes bosons, while Dirac's describes fermions.

So, as I say, he does not use the parallel axiom to prove that the two lines with a+b equal straight angle, do not meet. He rather proves this first. He uses the parallel axiom to prove the converse, i.e., if the sum is not equal straight angle, then they meet. Here:

The only such connection I see is, if the ASA for triangles depends on the parallel axiom. I don't know if it does. It seems that "it follows" of Stillwell is misleading, and all he wants to demonstrate is why Euclid postulates the case of a+b being less than two right angles. P.S. Nope, this understanding is also not right, because the next he says, "Thus Euclid’s axiom about non-parallel lines implies that parallel lines exist." How?

Where is an assumption that the parallel axiom is valid for a+b equal two right angles made? The only assumption made is that when a+b equal two right angles the lines meet, and this assumption leads to contradiction.

IOW, you also think that this statement of the parallel axiom does not apply in this deduction of the two described lines not meeting. There is no question of extending the parallel axiom statement to the case of straight angle. The question is, why Stillwell says, "it follows"? And this deduction does not use the axiom that if the sum of alpha and beta is less than two right angles then m and n meet. Or does it?

My question is, where this axiom is used in this deduction?