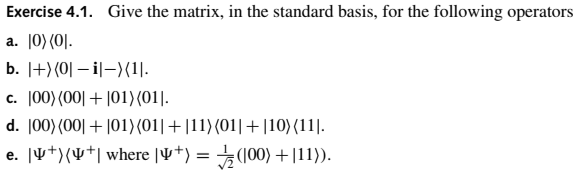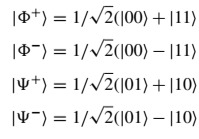Genady

To notarize my signature on a US document, it is easier for me to fly to Curacao and to do it in the US consulate there, then to do it with a Dutch notary here on Bonaire.

a. 1/√2(|0><0|+|0><1|+|1><0|-|1><1|) b. |0><1|+|1><0| c. |0><1|-|1><0| d. |0><0|-|1><1| e. 23|00><00|-5|01><01|+9|11><11| f. (|0><1|+|1><0|)⊗(|0><1|+|1><0|) = |00><11|+|01><10|+|10><01|+|11><00| g. (|0><1|+|1><0|)⊗(|0><0|-|1><1|) = |00><10|-|01><11|+|10><00|-|11><01| h. 1/2(|00><00|+|00><01|+|01><00|-|01><01|+|00><10|+|00><11|+|01><10|-|01><11|+ |10><00|+|10><01|+|11><00|-|11><01|-|10><10|-|10><11|-|11><10|+|11><11| i. P1 = |++><++| + |-- >< --| P2 = |+- ><+-| + |-+>< -+| Correct?

(From Rieffel, Eleanor G.; Polak, Wolfgang H.. Quantum Computing: A Gentle Introduction.) a. 1 0 0 0 b. = (|0>+|1>)<0| - i(|0>-|1>)<1| = |0><0| + |1><0| - i|0><1| +i|1><1| 1 -i 1 i c. 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 d. 1 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 e. = 1/2(|00>+|11>)(<00|+<11|) = 1/2(|00><00|+|00><11|+|11><00|+|11><11|) 1/2 0 0 1/2 0 0 0 0 0 0 0 0 1/2 0 0 1/2 All right?

Not surprisingly the form and the contents of their post above fit ChatGPT response well.

I wonder if the OP "Alej" and "Alessandro" are the same person.

For the reference, the Bell basis: a. = 1/√2(|Φ+>+|Φ->) b. = 1/2(|0>+|1>)(|0>-|1>) = 1/2(|00>-|11>+|10>-|01>) = 1/√2(|Φ->-|Ψ->) c. = 1/√3(1/√2(|Φ+>+|Φ->)+√2|Ψ+>)

I will ask, with respect to what decomposition?

|0>|+> + |1>|- > = |0>(|0>+|1>) + |1>(|0>-|1>) = |00>+|01>+|10>-|11> =(assume) (|0>+x|1>)(|0>+y|1>) = |00>+y|01>+x|10>+xy|11> This requires x=1, y=1, xy=-1, which is impossible. Thus, the state is entangled.

Let's assume it is not entangled with respect to such decomposition. Then it can be factorized (I skip the normalization factors for simplicity): |Wn> = (a|0>+b|1>)...(y|0>+z|1>) Then, this state would have a term, a...y|0...0>. But there is no such term. It means that a...y=0. Let's say, a=0. Then, |Wn> = b|1>(...)...(y|0>+z|1>). Then, every term would have |1> for the first qubit, which is not so. Contradiction. Thus, such factorization is impossible, and the state is entangled with respect to such decomposition.

Eastern District of New York | Congressman George Santos Charged With Conspiracy, Wire Fraud, False Statements, Falsification of Records, Aggravated Identity Theft, and Credit Card Fraud | United States Department of Justice

1/2*(|00>+|11>) + 1/2*(|00>-|11>) = |00>

(From Rieffel, Eleanor G.; Polak, Wolfgang H.. Quantum Computing: A Gentle Introduction.) Let's call vectors a=(1,0,0), b=(0,1,0), and c=(0,0,1) One answer is the basis {aa,ab,ac,ba,bb,bc,ca,cb,cc}. Let's take two different vectors in V: d=(0,sqrt(1/2),sqrt(1/2)) and e=(0,sqrt(1/2),-sqrt(1/2)). a, d, and e are orthonormal. The second answer is the basis {aa,ad,ae,da,dd,de,ea,ed,ee}. Of course, there are many other bases.

This is incorrect. Before the new road, any driver travels either by APB or by AQB, but not both. Their times do not add.

Doubtfully. The theory of relativity deals with the relation between space and time, while your geometry is only spatial.

What is "a root equation"?

The last part meant to be rather "never reached the Earth's escape velocity"?

Exercise 2.11. B92 quantum key distribution protocol. In 1992 Bennett proposed the following quantum key distribution protocol. Instead of encoding each bit in either the standard basis or the Hadamard basis as is done in the BB84 protocol, Alice encodes her random string x as follows: 0 ↦ |0〉 1 ↦ |+〉 = 1/ √ 2 (|0〉 + |1〉) and sends them to Bob. Bob generates a random bit string y. If yi = 0, he measures the i-th qubit in the Hadamard basis {|+〉, |−〉}, if yi = 1 he measures in the standard basis {|0〉, |1〉}. In this protocol, instead of telling Alice over the public classical channel which basis he used to measure each qubit, he tells her the results of his measurements. If his measurement resulted in |+〉 or |0〉, Bob sends 0; if his measurement indicates the state is|1〉 or |−〉, he sends 1. Alice and Bob discard all bits from strings x and y for which Bob’s bit value from measurement yielded 0, obtaining strings x' and y'. Alice uses x' as the secret key and Bob uses y'. Then, depending on the security level they desire, they compare a number of bits to detect tampering. They discard these check bits from their keys. a. Show that if Bob receives exactly the states Alice sends, then the strings x' and y' are identical strings. b. Why didn’t Alice and Bob decide to keep the bits of x and y for which Bob’s bit value from measurement was 0? c. What if an eavesdropper Eve measures each bit in either the standard basis or the Hadamard basis to obtain a bit string z and forwards the measured qubits to Bob? On average, how many bits of Alice and Bob’s key does she know for sure after listening in on the public classical? If Alice and Bob compare n bit values of their strings x' and y', how likely are they to detect Eve’s presence? My solution: To clarify the protocol, let's make the table: 1a 1b 2 3 4a 4b xi: 0 0 0 1 1 1 yi: 0 0 1 0 1 1 Alice sends: |0> |0> |0> |+> |+> |+> Bob measures: |+> |- > |0> |+> |0> |1> Bob sends: 0 1 0 0 0 1 Action: discard keep discsard discard discard keep a. As seen in the table, only the cases 1b and 4b are kept. In these cases, xi and yi are identical. b. Otherwise, they would keep the mismatched cases 2 and 3. c. Eve is only interested in cases 1b and 4b: 1ba 1bb 4ba 4bb xi: 0 0 1 1 Alice sends: |0> |0> |+> |+> Eve measures standard: |0> |0> |0> |1> Eve measures Hadamard: |+> |- > |+> |+> If she measured in the standard basis, the only unambiguous result was when she got |1>, case 4bb, which constitutes 25%. Similarly, if she measured in the Hadamard basis, the only unambiguous result was in case 1bb, also 25%. So, Eve knows for sure 25% of the bits, on average. Just like in the BB84 protocol, Eve sends to Bob 50% of the bits in a modified state. Of them, Bob will measure randomly a correct result in 50%. Thus, 25% of the final strings will differ. After comparing n bits, Alice and Bob will detect Eve's presence with 1-0.75n likelihood. Is it correct? I am not really sure in the last part. A table that includes what Eve sends to Bob and what Bob measures, would make the answer certain, but it is too much work.

Exercise 2.10. Analyze Eve’s success in eavesdropping on the BB84 protocol if she does not even know which two bases to choose from and so chooses a basis at random at each step. a. On average, what percentage of bit values of the final key will Eve know for sure after listening to Alice and Bob’s conversation on the public channel? b. On average, what percentage of bits in her string are correct? c. How many bits do Alice and Bob need to compare to have a 90 percent chance of detecting Eve’s presence? My answers: a. 0 b. 50% c. 0.5n < 0.1; n > 3 Is it correct?

(From Rieffel, Eleanor G.; Polak, Wolfgang H.. Quantum Computing: A Gentle Introduction.) Exercise 2.9. In the BB84 protocol, how many bits do Alice and Bob need to compare to have a 90 percent chance of detecting Eve’s presence? For the reference, here is a description of the BB84 protocol: My solution: If eavesdropping has taken place, then about 25% of the pairs of bits don't match. In this case, when Alice and Bob pick a pair at random, there is 75% chance to pick a matching pair. If they continue and pick n pairs, there is 0.75n chance that they all match. 0.758 = 0.1. So, if they compare 8 or more pairs, they have 90% or more chance to detect the eavesdropping.

The last one on this theme: My answers: a. 1/√2 (|0> - i|1>) b. 1/√2 (|0> - i|1>) c. 1/√2 (|0> - eiπ/6|1>) d. √3/2 |+> + i/2 |- > I am not sure what they mean by "all". I think that for each state there is only one orthonormal basis that includes that state, up to a phase. (In this case of the two-dimensional states, of course.)

Continuing the same theme: My answers: a. 3/4, 1/4 b. 1/4, 3/4 c. 1/2, 1/2 d. 1/2, 1/2 e. 1/2, 1/2 f. 1/2, 1/2 g. 1/8*(4+2√3), 1/8*(4-2√3) Does it look right? I am not sure what they mean "describe possible measurement outcomes". I think that the outcomes are just Yes or No for whatever is measured each time.

Next: My answers: a. π b, c. any

Mattock, sheep, rocket, clock?

E.g., OceanGate Inc. did not take such a risk.

Exercise 2.4: Which of the states in 2.3 are superpositions with respect to the Hadamard basis (|+〉, |−〉), and which are not? My answer: Superpositions: b, c, d, e. Not superpositions: a, f. OK?