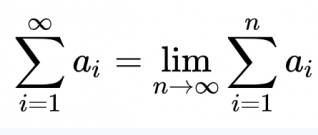Genady

In addition to the above, QC is not a general-purpose computer and it supposed to operate under instructions from a classical computer. The latter of course should have all usual protections.

The definition that I knew and have seen elsewhere is consistent with the definition in Manifold - Wikipedia: As you see, in this definition, manifold has sufficient structure for defining dimensions based on a continuous 1-1 correspondence, as per 12 lines above the beginning of paragraph 96 on page 162.

Any point 50 miles south of equator. According to the definition of manifold, it already has necessary structures, specifically, it has neighborhoods defined and, moreover, homeomorphic with Euclidean neighborhoods. It does not necessarily have a metric.

Since the question mentions numerical distances, I assume the manifold in question is endowed with a metric.

To make it more precise: There are points such that if the two people start their journeys (as described) in one of these points, they will be in the same place at the end. There are other points. If the two people start their journeys in one of these points, they will not be in the same place at the end.

There are points such that if the two people start their journeys (as described) in these points, they will be in the same place at the end. There are other points. If the two people start their journeys in these points, they will not be in the same place at the end.

If A.Guth is right, the positive potential energy which you describe in your comment might be countered by a negative energy of the gravitational field and the total might be 0.

It is not wrong. But three bars make it clear that it is a definition rather than an equation.

Here Alan Guth explains why he thinks that total energy of the universe might be 0. Starting at the minute 22 until about the minute 26:

Depends on the starting point.

I meant, yes, indeed some people consider the total energy in the universe to be zero. But I don't know what the "total energy in the universe" means. In some definition perhaps it might be zero. As "an infinite amount of energy", too. For example, if the universe is infinite in size and vacuum has energy, then there is an infinite amount of vacuum energy in the universe.

Yes. It depends on reference frame. As far as I can interpret it, it is correct. Yes.

Perhaps it might be clearer if instead of they have said

Because GR does not require an assumption of finite energy.

No.

Yes. This or similar, i.e., causality is a correct explanation of not moving faster than light rather than an infinite energy required for the acceleration.

He just does. Why not?

It is easy to prove that there is no solution. Here it is: The sum of 1/2^n from 1 to m equals 1-1/2^m. If there is a solution, then 1-1/2^m = 1, which means 1/2^m = 0. But 1/2^m > 0 for any m. Thus, there is no solution.

But you don't have to move an object. Instead of moving the object, pick an observer that moves faster than light relative to the object. The object moves faster than light relative to that observer.

This discussion, especially the reference provided here (https://www.scienceforums.net/topic/132322-spatial-dimensions/?do=findComment&comment=1249400) emphasized the importance of continuity assumption regarding coordinates, e.g., in these statements from MTW: and

n does not have a definite value in this expression. It runs from the lower bound of summation to the upper bound. There is no last point. There is no solution to the equation.

By definition, it means the following: for every real number d>0 there exists such natural number N that |(sum from 1 to m of 1/2^n) - 1| < d for any m>N.

Could you please point to the page in the book for this? (I mean, the page number)

Following this definition (Manifold - Wikipedia): @Markus Hanke: Since homeomorphism is a part of the definition, it does not require anything more to be in place for that to work. Right? If the boundary of n-dim region in Euclidean space is (n-1)-dim region, the homeomorphism caries this property into the manifold. @studiot: Dimensions are defined, through the homeomorphism, the same way as dimensions in Euclidian space, i.e., the mapping of neighboring points has to be continuous. Here is the procedure described by MTW: