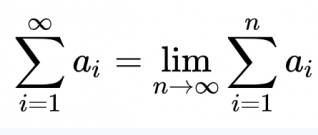Genady

Yes. It depends on reference frame. As far as I can interpret it, it is correct. Yes.

Perhaps it might be clearer if instead of they have said

Because GR does not require an assumption of finite energy.

No.

Yes. This or similar, i.e., causality is a correct explanation of not moving faster than light rather than an infinite energy required for the acceleration.

He just does. Why not?

It is easy to prove that there is no solution. Here it is: The sum of 1/2^n from 1 to m equals 1-1/2^m. If there is a solution, then 1-1/2^m = 1, which means 1/2^m = 0. But 1/2^m > 0 for any m. Thus, there is no solution.

But you don't have to move an object. Instead of moving the object, pick an observer that moves faster than light relative to the object. The object moves faster than light relative to that observer.

This discussion, especially the reference provided here (https://www.scienceforums.net/topic/132322-spatial-dimensions/?do=findComment&comment=1249400) emphasized the importance of continuity assumption regarding coordinates, e.g., in these statements from MTW: and

n does not have a definite value in this expression. It runs from the lower bound of summation to the upper bound. There is no last point. There is no solution to the equation.

By definition, it means the following: for every real number d>0 there exists such natural number N that |(sum from 1 to m of 1/2^n) - 1| < d for any m>N.

Could you please point to the page in the book for this? (I mean, the page number)

Following this definition (Manifold - Wikipedia): @Markus Hanke: Since homeomorphism is a part of the definition, it does not require anything more to be in place for that to work. Right? If the boundary of n-dim region in Euclidean space is (n-1)-dim region, the homeomorphism caries this property into the manifold. @studiot: Dimensions are defined, through the homeomorphism, the same way as dimensions in Euclidian space, i.e., the mapping of neighboring points has to be continuous. Here is the procedure described by MTW:

These questions cannot be answered with the currently known laws of physics. Even the phrase 'before the big bang occurred' does not have clear meaning, because time is defined in the universe which we observe, and which exists of course only after the big bang occurred. There are many theoretical suggestions to extend the known laws into these unknown territories, but for the lack of evidence, no one is better than others.

Yes, a simpler procedure is described in MTW on page 10. While they just describe it, clearly and 'obviously', I posted this question hoping that we can arrive to it or other(s) and clarify on the way what the minimal requirements and assumptions are. The starting point is that the 'space' is manifold. Since each manifold has a definite dimensionality, the question is well defined in this case. I am glad to have you guys participating.

Much obliged

It is not valid because GR does not allow it. Homogeneous isotropic space cannot be stable. That's why the prediction of expanding space happened a few years before Hubble's observations.

It could be an intrinsic property which adds to the expansion, but the large-scale expansion would happen without it anyway. The large-scale expansion happens without cosmological constant either.

It's a Mathematics forum

Right. Let's see. If we can mark points with a marker, and we have a piece of a line (a ruler with no marks), will it be enough?

I don't understand why it is needed. In GR, a universe homogeneously filled with inert dust, expands. My question is, in a universe with local inhomogeneities of such dust and thus not necessarily expanding locally, is the large scales expansion an emergent property?

Imagine that you are given a smooth space of unknown geometry. What kind of constructions would you use to figure out the number of dimensions of this space?

I don't know how to apply Gauss in this case. When gravity is described by a non-flat spacetime metric, what is the 'flux'?

I don't see why it would. (We cannot use Newton's law of gravity here. Expansion appears only in the Einstein field equation.)