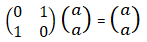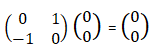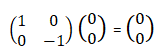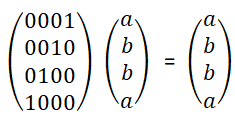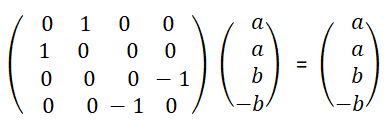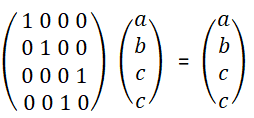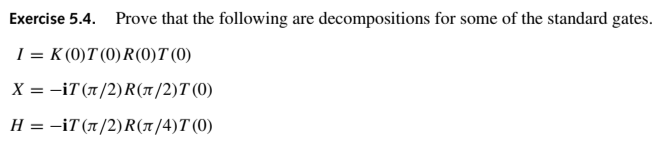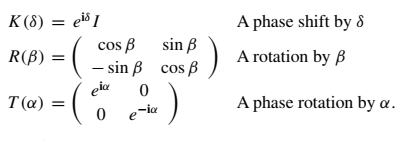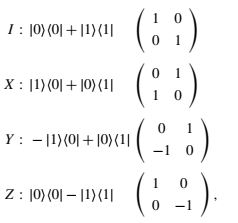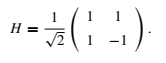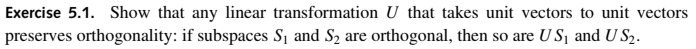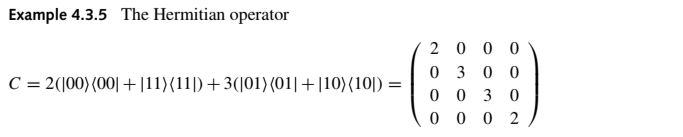Genady

Whose brain?

The OP is not genuine. It is plagiarized from https://www.physicsforums.com/threads/height-of-a-stable-droplet-on-a-perfectly-wetting-surface.1057037/post-6964327.

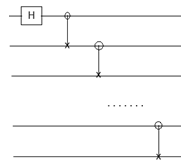
An n-qubit cat state is the state 1/√2 (|00 . . . 0〉 + |11 . . . 1〉). Design a circuit that, upon input of |00 . . . 0〉, constructs a cat state. ======== My idea is first to transform the first qubit to the superposition using the Hadamard gate and then to propagate the result to the rest of the qubits with the Cnot gates:

a. b. c. d. e. f.

For the reference: K(0) = T(0) = R(0) = I. Thus, K(0)T(0)R(0)T(0) = I. T(π/2) = i * 1 0 0 -1 R(π/2) = 0 1 -1 0 T(π/2)R(π/2)T(0) = iX. X = -iT(π/2)R(π/2)T(0). R(π/4) = 1/√2* 1 1 -1 1 T(π/2)R(π/4)T(0) = iH. H = -iT(π/2)R(π/4)T(0).

(From The New Yorker of October 23)

(For the reference, the BB84 is described here: https://www.scienceforums.net/topic/132653-quantum-key-distribution/) I assume that Eve always measures her qubit in the standard basis. Let's see what happens: 1. Alice's bit is 0. 1.1. Alice and Bob pick the standard basis. She sends |0〉. Eve applies Cnot: |0〉|0〉 ↦ |0〉|0〉. Bob gets 0. Correct. Eve gets 0. Correct. 1.2. Alice and Bob pick the Hadamard basis. Alise sends 1/√2(|0〉+|1〉). Eve applies Cnot: 1/√2(|0〉+|1〉)|0〉 ↦ 1/√2(|0〉|0〉+|1〉|1〉). 1.2.1. Bob gets 0. Correct. Eve gets 0. Correct. 1.2.2. Bob gets 0. Correct. Eve gets 1. Error. 1.2.3. Bob gets 1. Error. Eve gets 0. Correct. 1.2.4. Bob gets 1. Error. Eve gets 1. Error. 2. Alice's bit is 1. 2.1. Alice and Bob pick the standard basis. She sends |1〉. Eve applies Cnot: |1〉|0〉 ↦ |1〉|1〉. Bob gets 1. Correct. Eve gets 1. Correct. 2.2. Alice and Bob pick the Hadamard basis. Alise sends 1/√2(|0〉-|1〉). Eve applies Cnot: 1/√2(|0〉-|1〉)|0〉 ↦ 1/√2(|0〉|0〉-|1〉|1〉). 2.2.1. Bob gets 0. Error. Eve gets 0. Error. 1.2.2. Bob gets 0. Error. Eve gets 1. Correct. 1.2.3. Bob gets 1. Correct. Eve gets 0. Error. 1.2.4. Bob gets 1. Correct. Eve gets 1. Correct. Looks like Eve gets 75% of Alice's bits correctly and introduces 25% errors in the bits measured by Bob, the same as in the original scheme. Am I missing something?

My guess is that it is a result of evolution by sexual selection. Akin displays some birds make to attract mates.

I've made errors in the 'diagonal' part of the construction for the question 'd' above. One needs to be careful not to include diagonal terms in rows or columns which already have terms in them. Thus, the correction: /* diagonal */ |0+ 0-〉 〈0+ 0-| + |0+ 1+〉 〈0+ 1+| + |0+ 1-〉 〈0+ 1-| + |0- 1+〉 〈0- 1+| + |0- 1-〉 〈0- 1-| + |1+ 0-〉 〈1+ 0-| + |1- 0-〉 〈1- 0-| + |1+ 1-〉 〈1+ 1-| + |1- 1+〉 〈1- 1+|

They have eaten insects, too... And other not-so-attractive stuff.

Exactly. They indicate that there are no fruits there yet. So, for now, one should look for fruits somewhere else. Flowers should've been rather discouraging then.

Continuing exercise 5.2 above. d. Construct the operator as follows: U = /* required cloning */ |0+ 0+〉 〈0+ 0+| + |0- 0-〉 〈0- 0+| + |1+ 1+〉 〈1+ 0+| + |1- 1-〉 〈1- 0+| + /* transpose */ |0- 0+〉 〈0- 0-| + |1+ 0+〉 〈1+ 1+| + |1- 0+〉 〈1- 1-| + /* diagonal */ |0+ 0-〉 〈0+ 0-| + |0- 0+〉 〈0- 0+| + |0- 0-〉 〈0- 0-| + |0+ 1+〉 〈0+ 1+| + |0+ 1-〉 〈0+ 1-| + |0- 1+〉 〈0- 1+| + |0- 1-〉 〈0- 1-| + |1+ 0+〉 〈1+ 0+| + |1+ 0-〉 〈1+ 0-| + |1- 0+〉 〈1- 0+| + |1- 0-〉 〈1- 0-| + |1+ 1+〉 〈1+ 1+| + |1+ 1-〉 〈1+ 1-| + |1- 1+〉 〈1- 1+| + |1- 1-〉 〈1- 1-| e. This set includes c, thus impossible to clone.

It is obvious why bees and butterflies are attracted to flowers. But why do humans find flowers attractive?

a. U = 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 b. Same as a but in the {|+〉, |-〉} basis. c. If such U existed, it would transform U(|00〉) = |00〉 and U(|10〉) = |11〉. Then U(|+〉|0〉) = U(1/√2 (|0〉 + |1〉)|0〉) = 1/√2 (|00〉 + |11〉) ≠ |++〉, i.e. |+〉 would not be cloned.

(From: Rieffel, Eleanor G.; Polak, Wolfgang H.. Quantum Computing: A Gentle Introduction.) Take v in S1 and w in S2: 〈v|w〉 = 0. 〈Uv|Uw〉 = 〈v|U†U|w〉 = 〈v|w〉 = 0. Too easy.

Continuing exercise 4.21 above: c. Generally, if a measurement of the first qubit is H1 = a b c d and a measurement of the second qubit is H2 = x y z v then the measurement of the two-qubit system would be H = H1 ⊗ H2 = ax ay bx by az av bz bv cx cy dx dy cz cv dz dv The reference: The measurement A cannot be achieved by two single qubit measurements, because for ax = 0 either av = 0 or dx = 0, but in A, av = 1 and dx = 2. The reference: H1 = 1 0 0 π H2 = I The reference: The measurement C cannot be achieved by two single qubit measurements, because for ax = 2, av = 3, dx = 3, dv = 2 the ratio a/d = 2/3 and a/d = 3/2. The reference: H1 = H2 = 0 0 0 1

Yes, there are gravitational "grooves" which free falling objects follow. But these "grooves" exist in spacetime rather than in space. They are called, geodesics.

Continuing exercise 4.21 above: a (continued). This property is generally true because product of projectors is not generally a projector: (P2P1)2 = P2P1P2P1 ≠ P2P1, generally. b. If S2 is a subspace of S1 then P2P1 = P2.

a. Initial state |0〉. Measure in {|+〉, |-〉}. Let's say, the resulting state is |+〉. Now measure in {|0〉, |1〉}. The resulting state can be |1〉. This effect cannot be achieved by a single measurement. Assume such measurement exists: |1〉 = (a|0〉 + b|1〉) (a*〈0| + b*〈1|) |0〉 = |a|2|0〉 + a*b|1〉. Thus, |a|2 = 0, a* = 0, |1〉 = 0.

The reference: a. Projector onto the subspace of agreeing measurements is |v1v2〉〈v1v2|+|v1⊥v2⊥〉〈v1⊥v2⊥|. |v1v2〉 = (cos θ1 |0〉 + sin θ1 |1〉)⊗(cos θ2 |0〉 + sin θ2 |1〉) When it acts on |ψ〉 only the terms |00〉 and |11〉 survive, i.e., 〈v1v2|ψ〉 = 1/√2 (cos θ1 cos θ2 + sin θ1 sin θ2) = 1/√2 cos (θ1 - θ2) Similarly, 〈v1⊥v2⊥|ψ〉 = 1/√2 (cos θ1 cos θ2 + sin θ1 sin θ2) = 1/√2 cos (θ1 - θ2). Thus, the projection results in the state 1/c (1/√2 cos (θ1 - θ2) |v1v2〉 + 1/√2 cos (θ1 - θ2) |v1⊥v2⊥〉) with the probability c2 = cos2 (θ1 - θ2). b. θ1 = θ2 c. θ1 - θ2= π/2 d. θ1 - θ2= π/4 e. For these pairs, the θ1 - θ2 is either 600 or 1200 with cos2 (θ1 - θ2) = 1/4.

The reference: |v〉〈v|-|v⊥〉〈v⊥| = cos2θ|0〉〈0| + sin2θ|1〉〈1| + cosθsinθ|0〉〈1| + cosθsinθ|1〉〈0| - (sin2θ|0〉〈0| + cos2θ|1〉〈1| - cosθsinθ|0〉〈1| - cosθsinθ|1〉〈0|) = cos2θ|0〉〈0| - cos2θ|1〉〈1| + sin2θ|0〉〈1| + sin2θ|1〉〈0| cos2θ sin2θ sin2θ -cos2θ

Let's assume that the two qubits are unentangled. Then their state can be factorized, v⊗w. If the first qubit is measured by projecting its state onto the subspace spanned by v, its result will be certain contrary to the assumption that there is no such measurement. Thus, they are entangled.

a. An unentangled state can be factorized by single-qubit states as v⊗w. A single-qubit measurement can be represented by an observable Q⊗I. The measurement with Q would change v into v'. The measurement with I would leave w unchanged. The result would be v'⊗w, which is unentangled. b. Yes, e.g., a measurement with Bell states would produce an entangled state. c. Yes, e.g., such a measuring of any Bell state.

They are asking for an observable that embodies this measurement. That is the Hermitian operator built out of the combination of the projectors. The other numbers are just decimal representations of the binary sequences, i.e. 1=001, 2=010, 3=011, ... The observable |0><0|+|7><7|-(|1><1|+|2><2|+...+|6><6|) has an eigenspace with eigenvalue 1 of states with equal bit values, and another eigenspace with eigenvalue -1 of states with unequal bit values.

(Finishing exercise 4.16 above) e. Let's make an upper triangular matrix T=UAU-1. If A is Hermitian, then T† = (U-1)†A†U† = UAU-1 = T Thus, T is upper triangular and T† is upper triangular, i.e., T is diagonal. It has n orthonormal eigenvectors (1,0,...0), ... (0,...0,1) with the same eigenvalues as A. Then the columns of U-1 are eigenvectors of A. They are orthogonal. Thus, the direct sum of their corresponding eigenspaces gives the whole space.