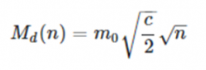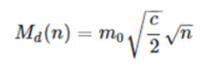Genady

Another question for you. In the definition, , the sqrt(n) is in the numerator. But in the "derivation" above, on the step 9, it is in the denominator. How come?

We are talking mathematics here. If you set c=v on line 5, you divide by 0 on line 6, and everything after that is meaningless. If you don't set c=v on line 5, then there is no c+c on line 6, and everything after that is wrong. You can decide, if you have it done or you haven't. The derivation is wrong anyway.

Yes, there is an error. After you set c=v on line 5, you get m0c/0 on line 6. Anything after that is meaningless, because there is no such thing as dividing by 0.

I've asked a mathematician and he wanted to clarify, if this is what you are saying: 1. M = m0 / √(1 - v^2/c^2) = 2. = m0 / √(c^2 - v^2)/c^2 = 3. = m0 / √(c + v)√(c - v)/c^2 = 4. = m0c / √(c + v)√(c - v) = 5. = √(c + c)√(c - v) = 6. = m0c / √(c + c)√(c - v) = 7. = m0c / √2c√(c - v) = 8. = m0√c / √2√(c - v) = 9. = m0√c / √2√n ?

I don't think your mathematical calculation is correct. To make it readable, break it down line by line. Then I think you will see an error.

What are the units on the left and on the right sides of the first equation, ?

However, there is no such problem in this case. YOU make the problem up.

No, I don't. E is a real number value. Infinity is not.

None. The equation does not have a solution for v=c. Just as it does not have a solution for v=2c, v=3c, etc.

Did you see my equation? There is no v=c in it. For every E, v<c. There is no infinity that needs to be made a sense of.

The equation is: v=sqrt(c2-m2c6/E2) Set E to any value in this equation and get v<c. No infinities anywhere! All values are finite! I do not "keep the value of infinity" at all, because it is not there! I don't need to "transform" anything "into a finite value", because all values are already finite!

Not true! I did not "refute that a particle can reach the speed of light by assuming that it cannot attain infinite mass/energy." This was what you keep saying, and I keep saying that this is wrong. Let me repeat again: I refute that a particle can reach the speed of light because any amount of energy can only accelerate it to a speed less than speed of light. Do you see a word "infinity" in what I say?

And I told you in my comment that there is no infinity in relativity. It has nothing to do with your theory. There is infinity in your misunderstanding though.

No, you did not answer my comment. My comment was about divergence, infinity, and 1/0. It was not about particles. Not observing particles at v=c is well explained in the theory of relativity.

Have you tested all particles with different energies, for example, by accelerating them using E=-(M(c-1)+m0^c^2) with c-1=299,792,458-1? The fact that we haven't observed such a particle is well explained here in M(c)=-M(c-1). The particle at v=c becomes undetectable. Each time you get a comment that you cannot answer, you change the topic. This means that you are not discussing in good faith. This means that you violate rules of the forum. I am reporting you.

There is no such a divergence. Take any v<c and you get a finite number. For v=c the formula you use is not applicable. You never get 1/0.

Dividing by a value close to zero does not pose a problem and does not require a solution.

It is very easy to eliminate it. Don't divide by 0.

A cosmological redshift of these distant galaxies has a magnitude of about 10. My back of the envelope estimate of gravitational redshift caused by a galaxy has a magnitude of about 10-6. The latter cannot significantly affect calculations based on the former.

It is quite straightforward to see why there is no area in this formula. Start with some area, weight, and frictional force. Now, make the area twice larger. The weight per square cm becomes twice smaller. But there are twice as many square cm. So, the frictional force per square cm becomes twice smaller but there are twice as many square cm. Thus, the total frictional force remains the same.

You are wrong. For example, the interval between any two events on null geodesic is 0. In physics. No, none of them equals infinity. Divergence is a feature of some integrals. 1/0 is a mistake.

No, nowhere in physics division by 0 is allowed. Regularization works with infinities that appear in divergent integrals, NOT in dividing by 0. Division by 0 is wrong in physics and mathematics alike.

You cannot divide by 0. It is an arithmetical mistake.

You are wrong. i is imaginary number. Both real and imaginary numbers are complex numbers. In 1+i you add two complex numbers.

By making arithmetical mistakes one can arrive to any conclusion one desires.