Genady

In the second case, there is a smaller amount of moving fluid to be stopped by friction. This makes a smaller amount of thermal energy.

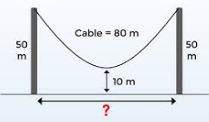
Maybe this little puzzle (see above) got lost between a heated debate in the Politics forum and an endless blabbering in the Speculations forum, but for whatever reason nobody has replied to it yet. So, I've asked ChatGPT. Again. Twice. Here are its spectacularly nonsensical answers. 1. To find the distance between the poles, we can use the Pythagorean theorem. Let's assume the distance between the poles is represented by "x." We have a right triangle formed by the distance between the poles (x), the height of one pole (50 m), and the length of the cable (80 m). The height of the lowest point of the cable (10 m) forms another right triangle with one of the poles (50 m) and the distance between the poles (x). Using the Pythagorean theorem, we can set up the following equation: x^2 + 10^2 = 50^2 Simplifying the equation: x^2 + 100 = 2500 x^2 = 2400 Taking the square root of both sides: x = √2400 x ≈ 48.99 m Therefore, the poles are approximately 48.99 meters apart. 2. To solve this problem, we can consider the triangle formed by the two poles and the center of the cable. Let's call the distance between the two poles "x". We have a right triangle where one leg is the distance from the center of the cable to the ground (10 m), the other leg is half the distance between the two poles (x/2), and the hypotenuse is the cable itself (80 m). Using the Pythagorean theorem, we can find the value of x: (10)^2 + (x/2)^2 = 80^2 Simplifying the equation: 100 + (x/2)^2 = 6400 (x/2)^2 = 6300 Taking the square root of both sides: x/2 = √6300 x/2 = 79.37 Multiplying both sides by 2: x = 158.74 Therefore, the distance between the two poles is approximately 158.74 meters.

Not yet, but it is in the line. I have three other books to read before its turn comes. I understand that it is a good book. I suspected so, that's why bought it to start with. I just don't see prime numbers having a very high priority in my education. Studying differential forms at the moment.

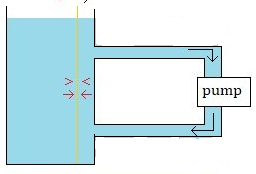
Or, like this: Yes, it seems that you are correct. The pressure on the right side of the wall is lower than on the left. The wall will move to the right and the water level on the right will rise.

Do you need a complication of the body moving up and down? Will your question change if there is no body, but instead you simply create a vertical stream of water on one side of the wall, e.g., by making a circulation through an external pipe?

Are you sure about it? My doubts are as follows: Although TM has an infinite tape, at any given stage of its run, only a finite part of this tape is in use. The infinity of the tape allows TM to use as much as needed, but it never actually uses an infinity of the tape. Physical computers are the same: at any given stage of their run, they use finite memory, but the memory can be, and is, dynamically added as needed.

OK. All I wanted to know is where you see the error. I know now. The error is not in the paper, but in your misinterpretation of it. I don't see any point in trying to convince you in this. And I am not interested in educating you. I got the answer to my question, and it is not interesting anymore. What you think about it never mattered. Have a good life.

This is again untrue. The speed of light as a definite number was called "c" before Einstein. And also on p. 3 Einstein calls it, "a universal constant".

So: You say that This is untrue. His approach is, from the page 1 of the paper, "that light is always propagated in empty space with a definite velocity c."

I have the paper linked above. There is no such a phrase there.

Does it break QM? If it does not, then it does not.

If they stay entangled, the correlation holds.

As long as the particles are entangled, results of their measurements are correlated.

Yes, I understand. When they are merely separated, they don't respond either. This is what I mean.

They don't respond in any case.

Another fun puzzle that is too hard for AI:

No, it approaches infinity.

Here is the Paper: einstein_electrodynamics_of_moving_bodies.pdf (umd.edu) Where is the Error?

IMO, you should compare cross-section areas rather than widths.

If the tube's diameter is almost equal to the ball's diameter, the velocity of the fluid near the ball's equator might be quite high, I think.

Perhaps, it was this: Solar panels - an eco-disaster waiting to happen? - BBC News There was a little discussion about it in the other thread: https://www.scienceforums.net/topic/131667-solar-panels-etc/?do=findComment&comment=1241447

I don't care about your respect. I care about physics.

Nope, your explanation was wrong then and it is wrong now. I understand - you don't.

For a contrast, here is the ChatGPT's latest attempt: Me: There is a table and two boxes. When the small box is under the table and the large box is on the table, the distance between the top of the small box and the top of the large box is 170 cm. When the small box is on the table and the large box is under the table, the distance between the top of the large box and the top of the small box is 130 cm. How tall is the table? Solve without algebra, if possible. ChatGPT: Let's approach this problem without algebra and solve it using logical reasoning. From the given information, we can determine that the distance between the top of the small box and the top of the large box is 170 cm when the small box is under the table and the large box is on the table. Similarly, when the small box is on the table and the large box is under the table, the distance between the top of the large box and the top of the small box is 130 cm. Now, let's consider the scenario where the small box is under the table and the large box is on the table. The total height in this scenario would be the sum of the height of the small box and the height of the table. Thus, we have: Height of small box + Height of table = 170 cm Similarly, in the scenario where the small box is on the table and the large box is under the table, the total height would be the sum of the height of the large box and the height of the table. Therefore: Height of large box + Height of table = 130 cm Now, let's subtract the second equation from the first equation: (Height of small box + Height of table) - (Height of large box + Height of table) = 170 cm - 130 cm Height of small box - Height of large box = 40 cm From this equation, we can deduce that the difference in height between the small box and the large box is 40 cm. Since we want to find the height of the table, we can determine that the height of the table is equal to the difference in height between the two boxes, which is 40 cm. Therefore, the height of the table is 40 cm.

Cool. This works, too. +1 And gives me idea for another trick: