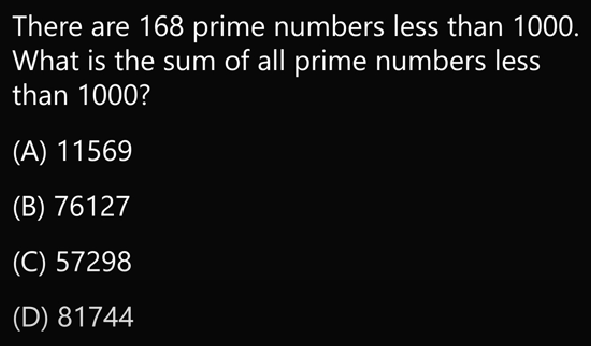Everything posted by Genady
-
Human Evolution
Taxons are specific. They are: Biologists are not free to call any bunch of things a "taxon".
-
Human Evolution
Not so in biology: Taxon | biology | Britannica.
-
Sum of Prime Numbers
I've stumbled upon this puzzle and immediately thought of @Trurl because they post about prime numbers often. Of course, others are welcome to try it as well.
-
An infinite vs a finite universe.
If a galaxy becomes not observable because of the universe expansion and disappears from the observable universe, where does it go? PS. Perhaps I misunderstood the idea of "repeating volumes of the observable universe". In this case, just ignore my question.
-
algebra
Where is it said? What is a duration of algebra? They are functions and operations.
-
Woodlpuse experiment
I see a problem. Experimenting with woodlice will not help you better understand effects of weedkiller on insects because woodlice are not insects.
-
James Webb Model at my Company
They didn't give enough space for a space telescope.
-
An infinite vs a finite universe.
How is it possible considering that observable universe does not have a constant size but rather changes with time? And considering that our observable universe differs from the one of a galaxy which is 10 bln ly from us.
-
Need help from any math people here with special relativity.
To transform between the proper time of the accelerating observer τ, and the stationary coordinates x and t, one can use ( Acceleration (special relativity) - Wikipedia ) : From x and v at the midpoint one finds the acceleration α, t at the midpoint, and then, τ at the midpoint.
-
An infinite vs a finite universe.
Re 1. No, I'm not saying this. Re 2. I take a spatial part of the spacetime metric.
-
An infinite vs a finite universe.
Yes. Firstly, I assume that the OP question refers to the spatial extent of the universe. Then, an infinite universe would be the one with infinitely many positions in it. An unbounded universe would be the one that for any number D there are positions with distance between them being greater than D. I think that the OP talks about the latter rather than the former.
-
An infinite vs a finite universe.
Evidence that physicists DO know the difference between infinite and very big, but finite is that they understand very well the difference between instantaneous action in Newtonian physics and very fast, but finite one in relativity.
-
An infinite vs a finite universe.
Technicalities aside, back to the original question, I don't think it will make any immediate difference, but it is something that is good to know. Might become handy at some point. Like extra savings in the bank.
-
An infinite vs a finite universe.
Just a technicality, but I think the question is not "infinite vs finite" but rather "bounded vs unbounded".
-
Human Evolution
This is right. I don't think at any moment we had any differences in understanding what actually happened.
-
Human Evolution
The issue then is what is the accepted understanding in science today. I think, it is: (Homo erectus, our ancient ancestor | Natural History Museum (nhm.ac.uk)) (Extinction of Homo erectus | The Smithsonian Institution's Human Origins Program (si.edu)) (Homo erectus | Definition, Characteristics, Skull, Diet, Tools, & Facts | Britannica) Etc.
-
Human Evolution
OTOH, Homo erectus - Wikipedia
-
Human Evolution
That would be extinction of a lineage. Extinction of species is different. Not necessarily evolution of differences, but different evolution. Even with the same selection pressures, separated organisms find different solutions and evolve along different trajectories. This is so speculative, that number of arguments one way or another is not only infinite, but uncountable.
-
Why can`t one sense god?
Interesting, I've missed that, but I posted it in this very thread also, here: Looks like we are "on the same page".
-
Human Evolution
Yes, dinosaurs and mammals are not species. Humans, i.e., Homo sapiens, are. So, my question was, "Do you assume that humans will not go extinct in the biological species sense?" Your answer is, yes. To me, the reasoning, "Most people would opt for their kids to be more normal, not more extreme" is not sufficient because of at least two issues: (1) Parents are not necessarily in control of this, and (2) What is considered normal is evolving as well. Even in this case, regarding the possibility of a total mix, would it happen before the humans split into distinct space colonies which will be separated from each other as or more than humans used to be by deserts and rivers?
-
Why can`t one sense god?
Not really, because it does not relate to any of my questions, does it? However, this does: Sense - Wikipedia. E.g., In relation to this thread's topic, as god is considered something that exists independently of human body, only the five external sensory systems are relevant.
-
Human Evolution
Yes, in the same sense that dinosaurs are extinct. Even if there will be some space dwelling monsters that are human descendants. Do you assume that humans will not go extinct in the biological species sense? Or do you rather talk about their descendant species? If these descendant species live in distinct space colonies, they are as or more isolated than humans used to be by deserts and rivers.
-
Human Evolution
But how long will it take? Is there any quantitative estimate? Would it happen before humans go extinct?
-
Why can`t one sense god?
What I think is arbitrary is which feelings to call "senses". For example, I feel that I'm getting older. Is it a sense? I know when I am irritated. Is it a sense? I know when I am awake. Is it a sense? And so on. One easy way to distinguish "senses" might be to classify them by external organs that response to stimuli. Then we got nose, mouth, eyes, ears, and skin. Obviously, this is as arbitrary as any other definition.
-
Can I delete such folders from C disk, example "02eeb6d92f89e33ba2ea06"
Why do you think so?