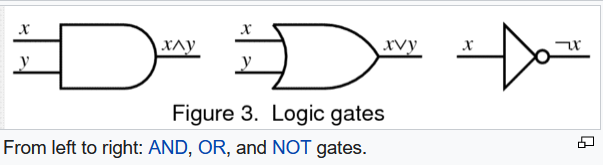Everything posted by SuperSlim
-
Surface waves in a liquid
So if my analysis is to proceed, it will be based on the different velocities of sound in solid glass, in water and in air. A vibrating wineglass or brandy bowl is definitely an acoustic chamber, because it's a bell made of glass. You could make some measurements and determine how good it is at amplifying sound waves. The vibrations in water, sitting inside the bowl of glass, are going to have internal reflections reinforcing the sound and amplifying it. The air inside the glass is a column, with pressure waves in it which are reflected and transmitted at the water surface. It's going to be a pretty complicated formula. But I could just concentrate on the liquid phase, and treat the rest as an input. The input has contributions from the solid and the gas phase the sound is propagating in. The real input is either some kind of bowing of the glass or an external speaker. Back to the question of inertia: does knowing the radius of gyration constitute a measurement? It's pretty simple for a thin disk of rigid material, and if that thin disk of material then curls itself up in a minimal way--to conserve something--it doesn't change the radius of gyration, but what about the amount of mass? The surface area has to increase to accomodate the periodic function.
-
Surface waves in a liquid
There are known formulas for waves on a surface, with two dimensions, which indicate to me that the radial pattern is a superposition of modes, a finite expansion. The minimal surface is definitely acting just like an elastic membrane. It deforms minimally by finding the greatest number of available modes, and filling them. The pattern is an eigenvalue for a sum of (abstract) wave vectors on a 2-dimensional surface with a circular boundary.
-
Surface waves in a liquid
So, after careful consideration, my opinion is that the Faraday standing wave pattern (with a smooth waveform at the boundary), is there because of the way sound propagates in different media There are three phases of matter involved: the solid glass in which stress patterns appear that can be visualized with the right spectroscopy; the liquid water in which sound propagates more slowly, but not much. then the air transmitting sound out of the cavity. The surface of the "newtonian fluid" gets saturated wth sound and the Faraday waves emerge, at resonance and with a stable bulk fluid. The reason the video I posted isn't a very good pattern, except at the edges, is because there is too much water; it's sloshing around so isn't a smooth sound transducer. But you can see those radial waves appear as the system approaches resonance; the sloshing could be avoided if there was a sound generator with variable frequency and volume, aimed at the glass.
-
Surface waves in a liquid
I think this example of Faraday waves on the surface of water might be entirely electrostatic. The fluid and its inertia contribute minimally, only the smallest part of the surface layer is responding. The restriction is the strength of hydrogen bonding at the surface. Another restriction for the overall system Hamiltonian--if we assume the pattern constitutes a measurement of something physical, i.e. information. Another way I look at it is an example of a periodic function, which is a smooth deformation of a manifold such that the surface area increases minimally, as a catenary "solution" to the input of sound. I think the water conducts sound waves so they reflect internally and build up to a feedback mechanism that contributes to overall resonance--and power output in the sound spectrum. It's an example of Baez' morphisms, that take surfaces to surfaces. We can easily construct such a 2-dimensional morphism from the boundary to the boundary, at--the boundary. A time independent function of two parameters, but which two? The morphism introduces a kind of system of coordinates on the surface.
-
Surface waves in a liquid
Yes, but I want to look into what the inertial fluid is doing inside the wine glass. The sound is driving some kind of inertial reaction, there's a surface layer of fluid interacting with sound waves, and it has a boundary where the fluid interacts with the vibrating glass. The fluid is responding to sound in a way that says something about inertia. I think I know what it is, but not exactly why it is what it is, if you see what I mean. Inertia is something you can relate to mass through the radius of gyration, it doesn't have to have angular momentum, but it has to be able to conserve it. If it did have some. What I'm leaning toward is getting my mate, if I can find him, to explain if Mach's principle applies, in an Einsteinian sense. This has to be a purely local effect.
-
Surface waves in a liquid
I found a video that demonstrates what I've been talking about. The result in the video isn't as stable as the one I got, which I put down to using less water and a crystal glass bowl with a better shape, to trap and direct the sound pressure-waves onto the water surface. If you stop the video when the pattern appears, you can see the boundary and a circle of individual rays. I think I've understimated the number which looks like it's over 100. Also notice how the radial pattern keeps appearing in the same position--but what fixes that? I'd say the video maker is using too much water and so there's turbulence, which tends to spread the fixed pattern out and distort it. I can vouch that this experiment, done properly, yields a nice, fixed, stable pattern. I wish I'd been able to take photos, but 'sigh', I didn't. With the example in the video the most stable pattern appears around 20s in. Otherwise it's a turbulent system with too much instability. https://youtu.be/3lRZQbXIdtc Ok, so I pencil in things like a unit volume V of water. It has mass and a density [rho] in kg.m-3 (I don't know how to insert Tex here). Then a differential volume dV, which inherits the physical units. So the mass is inertial and gravity is a downward force F = mg; the water is in a relaxed state inside a container which is a potential surface; the potential up the sides is gravitational potential and is parallel to the normal at the liquid surface. Usually in a 'stationary, relaxed' state we have forces in equilibrium so mg = kx, for x parallel to the normal direction. x has units of distance so dx exists, and k must have units kg.s-2
-
How can information (Shannon) entropy decrease ?
That's a generally true statement; don't forget a computer is a thermodynamic system, but one with constraints and restrictions; one of which is how information is represented, what is the computational basis. Thermodynamic systems don't generally have restrictions like that. A computer is based on an artificial choice, made by engineers, they are of course forced to choose something physical and deal with what nature has to offer (type of thing). That's why computers are not isolated systems; the computational basis has to live in a heat bath; the content of this bath has to be controlled which is another restriction on the system. You've already mentioned that entropy has various different formulations. Shannon entropy is a measure of the differences in information content between fixed messages; it's not evolutionary entropy. What that is is algorithmic entropy. This is related to the so-called shortest program that implements the algorithm. For instance a program that prints a single number, say 8, can do whatever it likes to calculate the value 8 as long as it outputs an 8. The simplest algorithm just prints an 8, but "the most complex algorithm which outputs an 8", is not well-defined . . . Algorithmic complexity has a Chaitin measure
-
Surface waves in a liquid
Thanks to certain mathematicians, like Laplace, Fourier, Euler and Lagrange, it is known that solutions exist for generalised wave equations. The surface of the water is initially just a region with a boundary, it's mathematically the real plane with a boundary, C; on the boundary you know the direction normal to this plane. You have certain boundary conditions apart from knowing the normal direction, you also know what the waveform looks like at the boundary, and you know the amplitude and how it changes from the boundary towards the centre. Because of the symmetry you only need to consider a single ray, you know the wavelength and that the number of wavelengths is a whole number. It's a problem that solves itself, except for the analysis. But you still need to determine what the initial conditions are, and how the system moves from one equilibrium state to another. It seems the excited state has only one solution, not dependent on the input frequency, but some fixed properties of the liquid.
-
Surface waves in a liquid
The surface of the fluid is fixed at a boundary too. It is a boundary value problem. Certain boundary conditions for waves have to be met. The glass bowl is a fixed, rigid container. It and the air in it are the reason it makes a sound you can tune with some water. And the idea, in analysis is to choose two parameters which may be interdependent. But this problem is about a waveform at a boundary and why it's there. What are the dependencies, apart from the surface tension and the inertia? You have to energise the surface with sound, it has to be loud enough and the surface big enough that a radial pattern appears. My guess is getting a pattern like the one I saw was a coincidence of a large enough surface area that the surface tension could contribute to the physics, and the right kind of resonant chamber. I would guess that smaller glass bowls--wineglasses--would be harder to make waves in.
-
Surface waves in a liquid
The problem is one of those B.v.p's that is independent of time; there is a fixed waveform, at the boundary there is an integral number of sine or cosine periods. Another thing I recall is, the location of the rays was the same if I repeated the rubbing, after stopping. I don't know, is that inertia or something? I'm guessing it's also independent of frequency, it's a passive response which seems capacitive and depends only on the amplification of sound in a chamber, it's got that nice linear behaviour in the summation of a set of standing rays.
-
Surface waves in a liquid
I guess you need to look at the fact a brandy bowl with some water in it is an acoustical chamber--you can change the pitch by changing the volume of water. Sound waves that exit the chamber dissipate; the water surface is reacting to the air vibrating inside the chamber + the vibration in the glass, these are in phase. So that determines what the forcing is--the acoustic chamber is an amplifier. It's like an upside down glass bell with water in it. And, the standing pattern doesn't change with time, but does it change with frequency? I tried this a few times on different days and I didn't see any real difference, I just used about the same amount, enough to get a sound and some waves.
-
Surface waves in a liquid
I would say the phenomenon is in the same class as a vibrating string, fixed at both ends. Except it's the vibrating surface of a glass bowl, transferring this vibrational mode to the surface of the water. How deep a layer is needed to see a regular pattern? I didn't look in to that, and I didn't look at different liquids, like say kerosene or light machine oil. I didn't try a thin layer of oil on top of the water, to investigate damping, say Nonetheless I know it's an example of a boundary value problem. with a unique solution. For water, that is. But I can't really see why other liquids wouldn't have unique solutions. How viscous does the liquid need to be to damp the response? Do more viscous liquids have the same number of rays as water (in the bowl I estimated about 50, the bowl was about 12 cm diameter at the liquid surface). The problem sort of demands that you see the surface of liquid water as having a boundary, it's "trapped in a cavity" and responds to forced oscillations. The pattern is fixed (I didn't see it rotate or oscillate at all). This is a repeatable experiment (!). Each ray will have an amplitude which increases from the centre towards the glass boundary, where it's a maximum. You know what the normal direction to the surface is, and you know the gradient of the amplitude of each ray; that's a boundary condition. No part of any ray (apart from the centre itself where all rays vanish), is tangent to a characteristic.
-
Surface waves in a liquid
Yeah, It is complicated. It is because the glass bowl is vibrating at a resonant frequency. The pattern seen on the surface of the water is a standing wave--it doesn't rise and fall as the finger moves around the glass. The entire surface is involved, as long as the glass is vibrating. It's a physics problem where you want to know the impedance of the oscillating systems. There's a transfer function for a system in resonance. Of course gravity is involved; when you stop moving your finger, the water relaxes because of gravity (mostly).
-
Surface waves in a liquid
Are you saying the surface waves that appear in a brandy bowl, are not an example of elastic waves? Can you demonstrate why that's the case (if it's true)?
-
Surface waves in a liquid
Yes, that must be true for a blob of water in zero gravity. When you place sand on a glass plate, the sand doesn't bounce around "elastically", although the glass plate does vibrate when you bow it with a violin bow. No wait, that's misleading. Of course particles of sand bounce around because they are elastic, solid particles. Frictionally damped liquids don't vibrate elastically, because friction damps the vibrations. No, wait . . .
-
How can information (Shannon) entropy decrease ?
Maybe the problem studiot posted would be easier to use if it was reformulated as a position/momentum problem. So it's like you know a particle is in one of N partitions. You know a particle can have one, and only one momentum (if it's classical). You have a two-parameter addressing mechanism that "reads" the contents of row i, column j. So it's like searching a memory for a "1" amongst a lot of "0"s. So it's down to what you can record, and how you record it. What does an algorithm that searches randomly need to do when it finds the particle? Is a brute-force, sequential search easier, since then you don't need to store information about empty partitions, just use a loop control. There's even a loop invariant! Also notice how it illustrates the difference between stored information, and an algorithm that searches for it (and changes local and global entropy). That seems kind of unavoidable (strong hint).
-
How can information (Shannon) entropy decrease ?
That's interesting. It's how Charles Bennett explains why Maxwell's demon doesn't get to store any information about gas molecules, and lower their information entropy. Except you haven't defined erasure of information. But that's ok, a computation doesn't need to erase information. I still don't get why you think I haven't addressed your questions. I think I have. I also think I'm possibly talking straight over your head. Look, I understand what Charles Bennett says about Maxwell's demon; I understand the concept and I understand what information entropy is. Here's a question, if I receive a message I'm expecting to receive, does it have more or less information content than a message I'm not expecting, but also receive? Can you answer it? Yes you have. My response to that is that it isn't a limitation; in fact the existence of a result of a computation has no bearing on whether a computation can run. Generally you seem to have some rather naive ideas about the subject; whereas I have at least 5 years of tertiary level study to rely on. Please don't try to convince me, or anyone else, that you know more than I do about computers; that's an argument you can't win. Sorry. It's possible you will never see such a thing. I predict you will continue to fail to understand what either kind of entropy actually is. I predict this because, here we are, and you still seem to be confused. A poster, joigus, has already said the two are "joined at the hip". That isn't an explanation, it isn't really all that enlightening, but it is true. Are you disagreeing with what he said, or just with what I said?
-
How can information (Shannon) entropy decrease ?
Part II Maxwell's demon doesn't get to violate the second law of thermodynamics because the identity transformation of a system of particles in thermal equilibrium, is a system of particles in thermal equilibrium. The demon can't read any information and just sees a continuous thermal background--a scalar field with constant value everywhere. So the Maxwell version of a demon doesn't get to store any information and lower its information entropy. If it could it could then violate the second law. Now I can put my feet back up on the desk, and heave a sigh of relief.
-
How can information (Shannon) entropy decrease ?
I'll throw in a hint here: the AND operation is not affine; but without it you don't have Boolean algebra; you need the AND operation to get a universal algebra. It follows that no set of affine logic gates is universal. This has consequences for quantum computation, according to Seth Lloyd at MIT. I guess he'd know. And I've seen a recent paper that claims to erase information without heat loss (a requirement of Landauer's principle), by using a bath of angular momentum, i.e. by giving the angular momentum stored in a qubit extra degrees of freedom. I'm not sure they really manage to escape the use of heat though, because the bath isn't thermally isolated. So have I gotten closer to an answer to the question: "how can Shannon entropy decrease?", by starting with what an increase (erasure) or decrease (storage) in local entropy means for isolated logic gates (?) By copying an input directly to an output the phase space volume is increased, there is "more room". In the phase space corresponding to information (something can be measured with probability 1, if a measurement is made), there's a function of position and momentum whose integral over both differentials is the identity transformation. The measurement Hamiltonian is an identity transformation of the position/momentum phase space. Maxwell's demon can't overcome this rule--to measure both the position and momentum of a gas particle, the demon must read information and store it.
-
How can information (Shannon) entropy decrease ?
I'm sorry too, that your attitude towards the subject of computation isn't very helpful to discussion. I didn't make an unqualified generalistic pronouncement, it was a qualified and relevant to the subject generalistic pronouncement, and I'm sorry if you haven't been exposed to a university-level education. In which one is pretty much required to question one's grasp of subjects, as much as possible; really thrash those equations. My counter to your argument, a Turing machine, FSAs and a string that doesn't change. I think that's quite a good one--nothing is erased, but where did the string come from? Doesn't there have to be a read/write head, and it has to move left or right? So it can do this over a fixed string for as long as you like, without halting, or if you want, with halting. Why do you give your counterexample the status of switching off the machine, is my next question. What does that erase on my tape? We haven't started discussing what reversible logic is. After all, according to an emeritus professor, when two logical paths merge, information is lost; this constitutes erasure. What better model than Boolean logic gates? I saw this used in an online lecture series to explain reversible logic. Part of the explanation involves the use of phase space volumes, and when do you "run out of room". Logic gates: The first two are two-input gates, the last is the unary negation operator. This last operator doesn't merge any inputs. What does the truth table look like when you keep one of the inputs, say the x input, and make the gate a two output gate? What you then have is a way to reverse the gate, logically. But there's a problem with how much information the x input can carry through to the outputs. You can also include the idea that the AND and OR gates with two outputs have memory--they each remember the x input (but locally!).
-
How can information (Shannon) entropy decrease ?
What are you talking about? You wanted me to answer a point about computation; there seems to be some dispute about whether an identity operation constitutes a computation. My question was, I think, why would you build a computer that does nothing? Why would you build a computer that leaves a string of symbols unchanged? Then I introduce FSA's and you respond by accusing me of not answering a different question about entropy. Can we focus on one thing at a time? Do you know what a finite-state machine is, have you done any programming? What languages? Can you code in assembly language? Have you written any languages or designed an instruction set, even for a simulated machine? I can answer yes to all the above.[ed: the third one's answer would be, "lots, or I can write one if that's what you need"] Can I ask, do you have any formal CS education, or can you maybe draw a diagram with logic gates in it? Otherwise, are you here trying to learn something? studiot: what do you think joigus is actually saying? What does what he says, if it's true of course, then say about what a computer is, as distinct from what a computer does? Also, I consider you as someone who perhaps hasn't discussed things like entropy, computation, what information is, and so on, very seriously before now. But I'm Captain Serious here when it somes to the subject of computers--I've studied a few CS subjects, more than most people. Well beyond what I'd need to do to get a job; in fact being employed in the industry was a lot like mowing lawns, in terms of what I could have been doing. But the money's real good.
-
How can information (Shannon) entropy decrease ?
Neither do I. It's something I aimed at your idea of a computer that only has an identity operation; the input is the same as the output. Perhaps you missed it. That's a somewhat simplified version of what a computation is; actually what that is is a way to classify computations: all those computations that have a known output and don't need to run again, plus all the computations that run again despite not having to. It might be a useful distinction, but it is only a distinction. But I see you have a way to go to. A computation is not something that comes with a fixed time to compute; we build "fast" computers, we get results "quickly", but that is a choice, it really doesn't affect what computation is. It doesn't affect what transmission of information is either.
-
Experiments and information
Are you trying to say the position and momentum of the electron that lost its kinetic energy to a screen is known? It's been captured? Captain Obvious rocks, eh?
-
How can information (Shannon) entropy decrease ?
Why does your question seem so bloody irrelevant? I wonder if Maxwell spent a whole morning figuring out whether to have his demon sit around doing nothing? I've just been shown a sign. It starts with Church and ends with Turing. A Turing machine that doesn't erase any symbols on a tape is equivalent to a finite-state acceptor; it accepts a string but if there's a programmed halt condition and a return to a "start of tape", that's an output, it's information. But not to the Turing machine itself, because it's just another symbol in an overall string which hasn't changed--the identity operation. If that's how you decide to define the identity operation. But it implies that all read-only Turing machines are just FSA's with the important distinction of the start-of-tape halt condition. That includes those machines that hop around, the FSA-only ones could hop around the string forever and never halt.
-
How can information (Shannon) entropy decrease ?
Ok. Maybe tomorrow if I can find the time. p.s. Please state exactly why you think building a computer that does nothing, so doesn't generate any heat, is a counterexample to what I said.