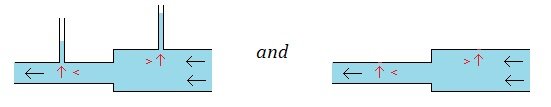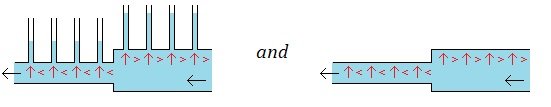zetetic56

I'm sorry for having tired you out. Thank you for your time. : ) Take care. : ) !!!

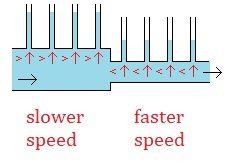
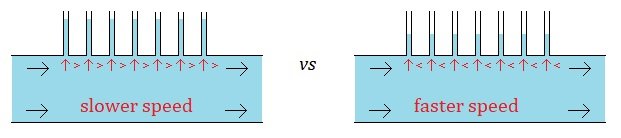
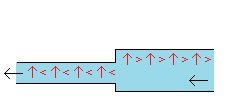
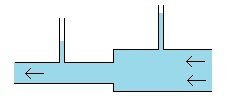
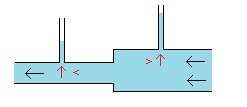
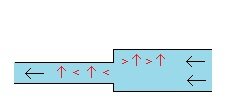
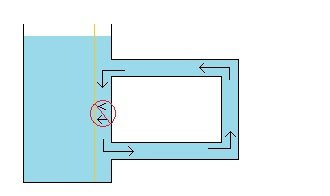
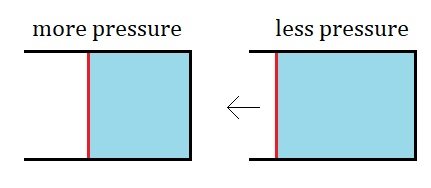
When a fluid goes from a tube with a larger cross-section into a tube with a smaller cross-section it speeds up. In Wikipedia it says: “Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or the fluid's potential energy.” And so, when a fluid goes from a larger tube to a smaller tube and speeds up there is also a “simultaneous ... decrease in static pressure or the fluid’s potential energy”. In a wind-tunnel (or a water-tunnel) the fluid can be moved through it slowly or the fluid can be moved through it quickly. The cross-section of the tube can remain the same, while the fluid moving through it can move slower or faster. (And we can assume this is done in a way so that the density of the fluid moving at the two different speeds is the same (and so there is no change in pressure from a change in density (mass per unit volume)).) And given that “Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or the fluid's potential energy”, This then means when a fluid in a tunnel with one consistent size cross-section is moved faster through that tunnel there is still a “simultaneous ... decrease in static pressure or the fluid’s potential energy”. If I’m reading the Wikipedia Bernoulli quote right, then when we move fluid slower or faster through the one sized wind/water tunnel, if there are pressure gauges on the top of that tunnel, then the readings on these gauges will be more when the fluid is moving slower and the readings on the gauges will be less when the fluid is moving faster. (?) On the left, the fluid moving faster through the smaller part of the tube will put less pressure on the walls of the tube than the fluid moving through the larger part of the tube. While, on the right, the same thing occurs, and the fluid moving faster through the tube will put less pressure on the walls of the tube than the fluid moving through the same tube slower. “[A]n increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or the fluid's potential energy.” And the “decrease in static pressure or the fluid’s potential energy” manifests as a decrease in the pressure from the fluid on the walls of the tube it is moving through. (Or so I think.) When a fluid is at rest and then is moving at some speed, this is an increase in speed (from 0 to something). And so when a fluid is moving, as opposed to being at rest, there is “simultaneously ... a decrease in static pressure or the fluid’s potential energy”. If we think of every point on the tube walls as potential pressure gauges, then “when there is movement of a fluid within a solid body there is less pressure on every point of the surface of the solid body from the fluid” seems to me to be correct. But maybe I haven’t made my case, and maybe we still disagree. (And maybe I’m still getting something wrong.) (?) Thank you and cheers. : ) !!!

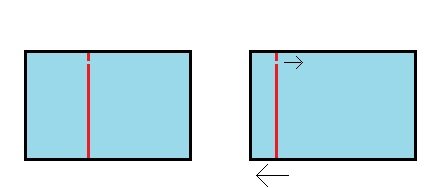
We seem to agree that, just as with pressure gauges, that with fixed walls, that at a point in the smaller tube with the faster moving fluid there will be less pressure from the fluid on the fixed wall while at a point in the larger tube with the slower moving fluid there will be more pressure from the fluid on the fixed wall. And so the same reasoning would lead to the idea that if we had several pressure gauges at several points then they would all show the lesser and greater amounts of pressures at each of these points, and so we would also have the same lesser and greater amounts of pressures at these same points with fixed walls instead of pressure gauges. And taking this same logic a step further, we could theoretically have a pressure gauge at every possible point along the fixed walls of the tube and so we would have this same lesser and greater pressures at every point along the fixed walls of the tube themselves. And so we end up with the logical conclusion: when there is movement of a fluid within a solid body there is less pressure on every point of the surface of the solid body from the fluid. Yes? No? According to Google the definition of a “flow regime” is “essentially a description of the flow structure, or distribution of one fluid phase relative to the other” and is also referred to as a “flow pattern”. So in the larger tube we have one “flow regime” and in the smaller tube we have a different “flow regime”. And if the velocities of the fluid moving through each of the two tube sections are constant and do not change with time, then we have two “steady state” “flow regimes”. (If i’m using these terms right.) And so, if we think in terms of “flow regimes” then it seems like we’d end up with the idea that where two “flow regimes” are different in how fast the fluid moves along the solid boundary walls containing them then the faster the fluid moves the less the pressure from the fluid is on every point of that boundary wall. (Again, if I’m using these terms right.) What do ya’ think? What am I still missing? Thank you. : ) !!!

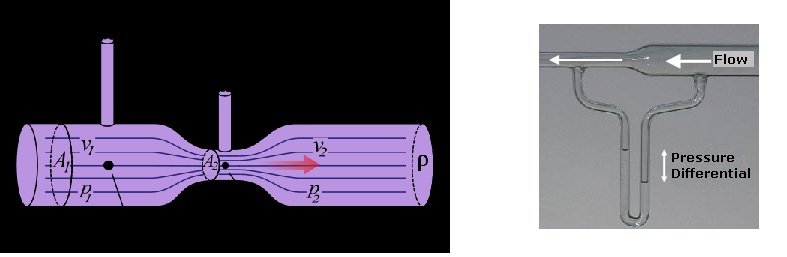
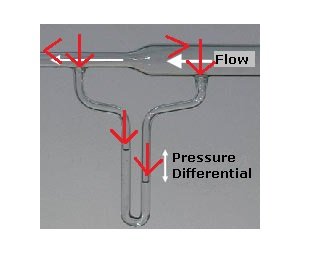
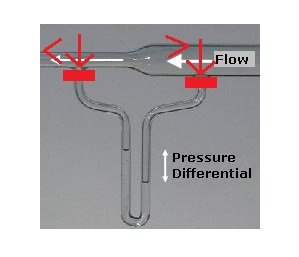
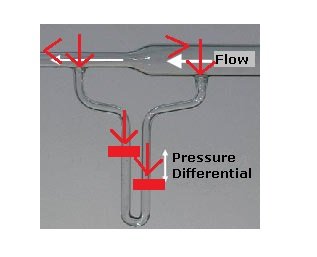
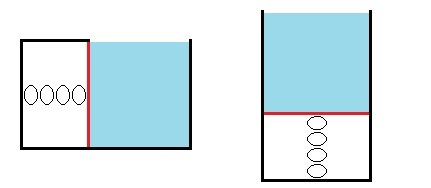
The two above pictures are from the Wikipedia page on the "Venturi Effect". The picture on the right is labeled as a "Venturi Meter". In the drawing above on the right, the U shaped tube below the pipe is labeled as a "manometer". And according to Google a "manometer" is defined as: "an instrument for measuring the pressure acting on a column of fluid, especially one with a U-shaped tube of liquid in which a difference in the pressures acting in the two arms of the tube causes the liquid to reach different heights in the two arms." In that "manometer" there is one fluid (presumable air) pushing down on another fluid (presumable water). The lesser pressure from the fluid moving faster through the pipe and the greater pressure from that fluid moving slower through the pipe have an affect on the other fluid at the bottom of the U and shift it. If there were two solid moveable walls resting on the top of the other fluid at the bottom of the pipe, my guess would be that we would get the same affect. My guess is that the differences in pressures from the fluid would affect a solid they are in contact with just as much as they directly affected the another fluid before the walls were added. And if those moveable walls were moved to the top of the two ends of the "manometer" then I would expect that the lesser pressure in the faster moving fluid and the greater pressure in the slower moving fluid would also affect these solid moveable walls (now in line with the walls of the pipe that the fluid is flowing through). And so if we removed the "manometer" and fill in the two open ends where the tops of the "manometer" were with just solid walls, then the same lesser and greater pressures from the fluid would also be lesser and greater pressure on the the two fixed in place walls. This is my reasoning and this is why I believe that when a fluid moves faster through a tube it puts less pressure on the tube's walls while when a fluid moves slower through a tube it puts more pressure on the tube's walls. I think my logic is right, but perhaps there's some underlying piece of Physics that my uneducated self is missing. ( ? ) Thank you for reading this. : )

Maybe. I understand from looking at, but not studying, the technical aspects of Bernoulli's Principle, that it appears to me there are different ways to think about it and there were probably some early Physics classic debates about it and there may be different technically important ways to understand it. And all of that is nothing that I know about or understand at all. I think visually, and here is how I have understood and defined "Bernoulli's Principle" for myself. When fluid moves across the surface of a solid body, the pressure from the fluid on the body decreases. And the greater the movement the greater the decrease in pressure from the fluid on the body. This is true when the fluid moves around the body. And this is true when the fluid moves through the body. And the two things above are really just the same thing. And maybe I'm wrong about this. This is how I've made the basic idea of Bernoulli's Principle make sense to me. And even if I'm not wrong about this (and maybe I am) I could still be using the term "Bernoulli's Principle" wrong (and perhaps I'm saying something different). --- When water moves though a pipe with different sized sections, it is my understanding that the fluid will move slower in the larger sections and faster in the smaller sections, and it is my understanding that there is a decrease in pressure with the faster moving fluid, and it is my understanding that the pressure from the fluid on a pressure gauge will show this. And so the lesser and greater pressures from the fluid do affect the pressure gauge and we get readings. And I would expect if there was not a pressure gauge there but a wall that the same decrease in pressure from the moving fluid on the pressure gauge would also be the same decrease in pressure from the fluid on the wall at that exact same spot, as well as an equal decrease in pressure on all the points along the walls. This is my reasoning. This is why I think there is decreased pressure on the walls when the fluid moves along the walls. But, maybe I've gotten far off base here and maybe I'm missing some fundamentals. Thank you and take care. : ) !!! --- Where's my delete key? Some times I find myself in metaphorical loose-orbit around the Moon. Apologies. Thank you and take care. : ) !!!

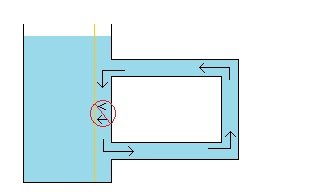
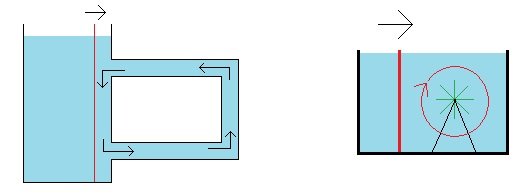
My common sense understanding of Bernoulli's Principle is when a solid moves through a fluid or when a fluid moves through a solid that there is a pressure decrease on that solid body from the fluid. There are different ways of looking at a rising aircraft wing and one of those ways, I understand, is to look at the greater decrease in pressure pushing down on the top and the lesser decrease in pressure pushing up on the bottom due to the more round top and more flat bottom when the wing moves horizontally. I don't know much about airplane wings, but if the fluid in the wind tunnel passing by the wing could pass by the wing without having a greater decrease in downward pressure and without having a lesser decrease in upward pressure, I cannot see the mechanics of this lack of an affect could occur. The reason why I said "it makes no sense to me" is that I cannot see how a moving fluid on along solid could sometimes have an affect (one way of describing a rising airfoil) and could sometimes not have an affect (the circulating fluid moving along the moveable wall to the side). It seems like Bernoulli's Principle would either just work in each case or not work in each case. I can't see the logic to distinguish where Bernoulli's Principle of less pressure when the fluid is in motion has an affect on the solid from when it does not have an affect on the solid. This is where my thinking is at. Thank you. : ) !!!

I didn't understand your use of terms "inside the flow" and "outside the flow". Apologies. Are you saying that it is possible for the fluid to move relative to the wall and to not have a pressure decrease from the fluid on the wall? I don't think that make sense. But maybe there is something I'm missing and/or misunderstanding. ( ? ) Thanks. : ) !!!

If I understand you correctly, you are saying that it is possible that when a fluid goes from being at rest inside a circular tube to being in motion, that while there is a decrease in pressure within the moving fluid, that it is possible that this decrease in pressure does not affect the pressure of the fluid on the solid wall that the fluid is moving relative to. Then is it possible that if there is an airfoil in a wind tunnel that as the fluid moves over the top and bottom of the solid body that while there is a pressure decrease in the moving fluid itself that this pressure decrease does not affect the pressure of the fluid on the solid body of the airfoil that the fluid is moving relative to? That doesn't sound right to me. Or perhaps I did not understand your response? Thank you. : ) !!!

"[T]he Bernoulli Principle, which states that the speed of a fluid (air, in this case) determines the amount of pressure that a fluid can exert." - nasa.gov It is my understanding that when a solid body moves through a fluid and when a fluid moves through a solid body (a pipe), when there is relative motion, and if the solid and the fluid are in contract with one another, then this means the pressure from the fluid on the solid decreases (and the faster the relative motion the greater the decrease in pressure). Your reasoning that there will be a pressure decrease on the right side of the wall as the fluid is moving relative to it, seems solid logic, given my basic understanding of Bernoulli's Principle, to me. (?) Thank you. : ) !!!

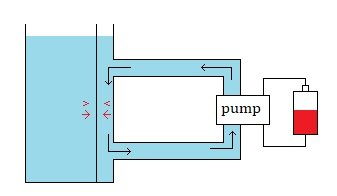
I did. I thought we were in agreement about this, but maybe not. I thought we agreed, but maybe not. The force that circulates the fluid comes from the pump. Is this not "external"? There may be a technical definition of "extremal force" in Physics and I just need to learn the mechanics of this and how it works. (?) Thank you. : ) !!!

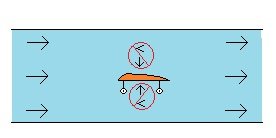
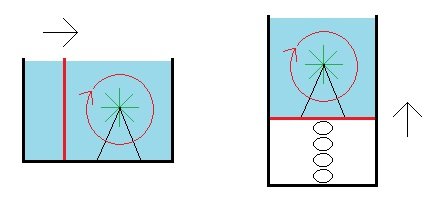
Hmmm? These are the steps in my reasoning: If the wall will move to the right when the fluid is circulating around in the pipe and so is moving relative to the wall, then I would think if the paddle wheel was immerse in a fluid in a cup where there is a movable side wall as well that the same logic would apply and the wall with the circulating fluid would also move to the right. And if the side wall would move to the right when the fluid is moving relative to the wall and the pressure from the fluid decreases, then I would expect the same pressure decrease when the fluid moves relative to a moveable floor and so (my reasoning) is that the spring will decompress. That's how I ended up where I am on this. Perhaps there's some bit of Physics that I am missing here. Or perhaps I just don't understand the point. Thank you for your time. : ) !!!

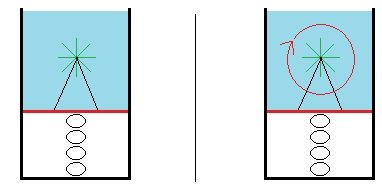
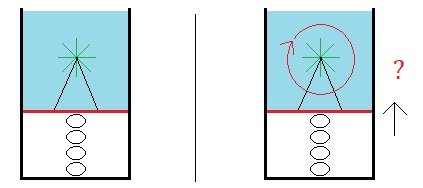
If it makes sense to mechanically think of the force compressing the spring is from the downward pressure from the fluid, then If there is a paddle wheel immersed in the water and fixed in place connected to the movable floor, and if we have two systems with the same thing, but in one system the water is not being circulated around inside the open topped cup while in the other system the water is being circulated around inside the open topped cup, and so there is a decrease in downward pressure in the one case and not this decrease in the other, then will the compressed spring be less compressed in the case where the fluid is moving? The area of the floor remains the same in both cases, but in the one case the amount of pressure pushing down on the floor decreases. If it mechanically makes sense to think of the spring being compressed by the downward pressure in the fluid, then I would think that the spring will decompress in the case where the fluid is moving around. (?) What do ya' think? Thank you and cheers. : ) !!!

I think I understand what you're saying. What I was thinking about was a case where the fluid's ability to flow upwards is in some way restricted. But maybe I just misunderstood the conversion you two were having. Or maybe such a restriction is irrelevant and I need some more Physics studying. : ) Apologies for weighing in and not adding to the conversation. Thank you. Downward pressure (amount x area) is equal to the weight, cool, that makes sense. Weight and downward pressure are equal amounts. What I'm wondering is this: There is a force pushing down on the spring. Would we say "this force is from the downward pressure from the fluid" or would we say "this force is from the gravitational attraction between the fluid and the Earth below"? Thank you. : )

If gas is in a chamber and a wall is pulled out then there will be less pressure. If there is a little hole in the moveable wall and if there is fluid on the other side of the wall, then since the fluid will not flow through the little hole and into the expanding chamber instantaneously, it will take a moment, it seems to me like for a moment (a very brief moment) there will be less pressure in the expanding chamber. If I understand your point correctly you were thinking about something like this but falling due to gravity. (?) If so, I think the same logic would hold, and there would be a brief moment of less pressure above the falling piston. Well, that's my guess. --- This is my favorite perpetual motion machine. When I first saw it I thought it worked. But then I learned some basic physics and realized why it doesn't work. There is a wheel resting on a central axis that it can rotate around. The wheel is half submerged in a fluid and is half outside the fluid. And so there is an upward buoyant force on one side of the wheel and not on the other. And so it seems like it will rotate counter clockwise and it will keep rotating forever. But then I learned some basic Physics and found out that the pressure from a fluid on a submerged body has direction and its direction is perpendicular to the surface of the body. And so, while there is more pressure on the right half of the wheel at its bottom and less pressure on its top, all of this pressure, because this is a circle, is directed at the central axis. There is an overall upward buoyant force on the right side of this wheel, but there is no torque, there is no twisting force around the central axis. And so, my favorite pmm does not work. --- Question: On the left, there is a open topped container filled with a fluid and it has a moveable wall on its side. On the other side of the moveable wall is a compressible spring. I think in the left case we would say where are measuring the "pressure" of the fluid against the wall. And then on the right there is another open topped container fill with a fluid and a moveable wall. And this moveable wall is the floor. And underneath the moveable floor is a compressible spring. And I would think we would say in the second case we are measuring the "weight" of the fluid. Right? Question: Can we measure the "downward pressure" from a fluid on the bottom of an open topped container or would we always end up measuring "weight"? --- Cheers. : ) ! [ Edit: Above I wrote "If so, I think the same logic would hold, and there would be a brief moment of less pressure above the falling piston." And didn't express myself right. As the tube falls and the chamber above expands, there will be brief moment followed by brief moment following by brief moment. And so it would be this slight less pressure above the piston as the piston falls. The "brief moment" of the fluid moving through the hole and into the expanding upper chamber will happen again and again and again. Sorry I didn't really say it right the fist time. I think this is better. : ) ]

Okay. Well thank you for looking at it. : ) Cheers. : ) !!!