zetetic56

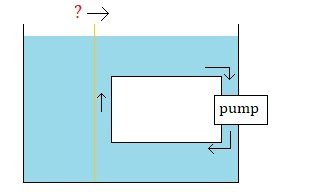
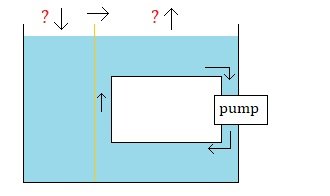
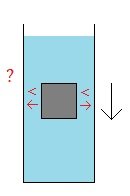
Here is what I think is interesting about the "moveable wall" question. Up to this point I think my questions are pretty obvious and simple and so I have guesses about all of their answers. This part of the moveable wall question, however, I do not have a guess at an answer. Say we have this system, and in this system the wall does not move. We start out with X amount of energy in the battery. The pump is run until the battery is drained. And while the pump is running the fluid moves and there is a decrease in pressure on the right side of the wall. The wall is fixed in place and so cannot move. In the end, after the battery is drained, and after the moving water comes to a stop due to friction, we end up with an increase in thermal energy. The X amount of energy in the battery is gone, and there is an increase in X amount of thermal energy. All makes sense (to me). Then the same thing is done again. But this time the wall can move. The wall here can move one way. It can move from left to right, but its kept from moving back right to left. Just like before, we start out with X amount of energy in the battery. The pump is run until the battery is drained. And while the pump is running the fluid moves and there is a decrease in pressure on the right side of the wall. The wall is not fixed in place and so can move. Due to the difference in pressures on the two sides of the wall, the wall moves from left to right, and the height of the column of fluid on the left goes down while the height of the column of fluid on the right goes up. There is an increase in gravitational potential energy. (The negative gravitational potential energy becomes less negative.) Say the increase is Y amount of energy. In the end, just as before, after the battery is drained, and after the moving water comes to a stop due to friction, we end up with an increase in thermal energy. However, here, in the end, we also have an increase in gravitational potential energy. And so, the X amount of energy in the battery is gone, and there is an increase in Y amount of gravitational potential energy, and so, for energy to be conserved there must be less of an increase in thermal energy, there must only be an increase of X - Y amount of thermal energy. This does not make sense to me. Question: Why would the wall moving due to a difference in pressures on the two sides of the wall and pushing the fluid on the right side of the wall up (as opposed to the wall staying in place when there is a difference in pressures on the two sides of the wall and the fluid on the right side of the wall is not pushed up) cause a decrease in thermal energy in the end? What is the physical dynamic that would result in less thermal energy being generated when the wall moves and pushes the fluid up as opposed to when the wall remains in place and does not push the fluid up? Thank you. : )

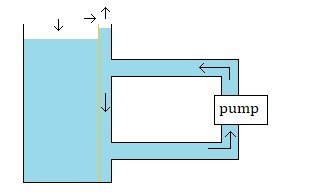
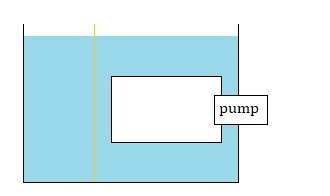
Thank you for confirming my suspicions. The logic seems pretty straight forward: there will be a difference in pressure on the two sides of the wall, and so the wall will move to the right, and so the column of fluid on the left will get lower and the column of fluid on the right will get higher. It seems pretty simple and its my guess that this is what would happen. Thank you. --- As an aside: I proposed this set up as purely a theoretical thought experiment. If this were to be built the difference in height as the submerged body rises (or falls) would probably be so small so as to not really be noticeable by our human eyes. But a pump could move the fluid fast. And this set up could potentially produce a height difference that is noticeable by us human beings. (I realized I should have the fluid moving down along the wall, instead of up along the wall (the way I first drew it), so that the pump isn't pushing fluid up on the higher side and so its just pressure differences resulting in the differences in height.) --- Thank you for continuing to consider my question. : ) !!!

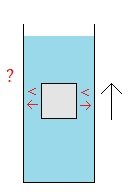
I think it would be the same question. Before the pump is turned on the fluid is static on both sides, and there is the same level of water on both sides of the moveable wall. The water is then circulated on one side of the wall, while the water remains static on the other side of the wall. The question is: will the wall move? And my guess is that the answer is "yes" (assuming no friction, or assuming a small enough amount of friction, with the moving wall). And so, it seems like we would end up with my same question. Would this scenario cause the water level to fall on the one side of the wall and rise on the other side of the wall? It seems to be the same basic question. Perhaps its easier to think of it differently than how I first conceived of it. : )

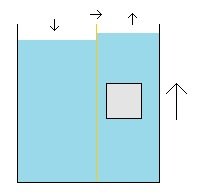
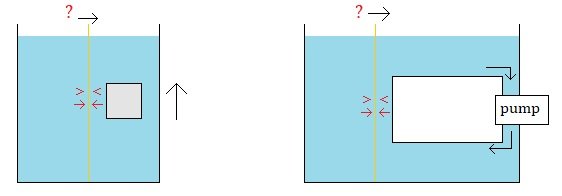
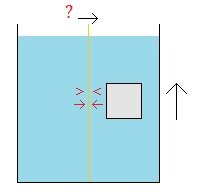
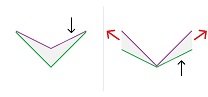
Up to this point my two questions seem to have fairly obvious answers and are not very interesting questions. This was leading to a (I think) more interesting question, but I wanted to establish that I had gotten the underlying physical dynamics correct first. 1. When a body rises in a column of fluid, is there a decrease in pressure on the container walls? and 2. Is this decrease in pressure not just negligible? My guess is that the answers to those two questions are "yes". But, again, I could be wrong. If they are "yes", then here is what I think is the more interesting question: There are two containers of fluid with a wall between them (or, same thing said differently, there is one container of fluid with a wall in the middle). The wall between them (orange) is moveable. It can move back and forth horizontally. There is a submerged buoyant body at rest in one of the containers. The columns of fluid are the same height on both sides of the moveable wall. The less dense body is allowed to rise in the more dense fluid. It is, again, on one side of the moveable wall. If 1. The pressure on one side of the wall decreases and 2. If this decrease in pressure is not negligible then 3. Does/will the the wall move? (The movement of the wall could be considered frictionless for the purposes of this thought experiment, or the amount of friction could be considered to be very small and less than the force from the difference in pressures on the two sides of the wall.) This is my main question. And this is what (I think) is the interesting question. [ If the answer is "yes" and the wall moves, then the height of the one column of fluid with the submerged body will rise while the height of the other column of fluid will fall. And this is what (I think) is interesting (if this is what will occur). ] --- I realize I am a guest in your home. I do appreciate you letting me post my questions here. And I do appreciate your time and the feedback you have given me. If there is no interest in replying to another one of my questions, I understand. Thank you all for your time and feedback you have given me (on this question as well as on my other questions I have posted previously). Thank you and take care : ) !!!

When a more dense body falls in a less dense fluid the fluid is displaced upwards and moves around the body and will also end up moving relative to the container walls. And so, it seems, like the pressure from the fluid on the container walls will decrease and there will be less pressure on the walls from the fluid than when the fluid was static. [ And thank you studiot for suggesting that my simplistic reasoning here is "essentially correct". ] And the same (or so it seems to my reasoning) would occur when a less dense body rises in a more dense fluid. As the fluid is displaced (or falls) downwards around the rising body it also moves relative to the container walls and so the pressure from the fluid on the container walls would decrease and become less than when the fluid was static. And my guess is that this decrease when a body rises or falls would be detectable and noticeable, and if there was some sort of pressure gauge on the container walls this change in pressure would be noticeable and not just negligible. But, right now, that is just my guess. Question: Is there a decrease in pressure on the container walls from the fluid when a body rises or falls within the fluid (as opposed to the amount of pressure from the fluid when it is static), and, if so, would this decrease more than negligible? Thank you guys for considering my question. : )

IMO you are right. I was thinking in terms of my 2 dimensional drawing. 3D is correct. Thank you : )

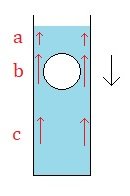
I think my previous "a" "b" "c" stuff is probably more confusing than helpful (and just flat out wrong in places). Now this is what I am thinking: Just as a matter of pure geometry, if the width of the falling object is the same as the width of the space between the object and the container, then the speed of the falling body will be the same as the speed of the rising displaced fluid around that body. As the same volume moves down the same volume must move up. (And if the widths of the falling body and the space between the body and the container are different from one another then the speed of the falling body and rising fluid will be different from one another, with the one with the greater width moving slower and the other one with narrower width moving faster.) Right?

If there is movement of the column of fluid above and below the falling body (the fluid at "a" and "c"), then I could see that being very slow. I could see the possibility that the change and decrease in the pressure on the container from the fluid could be negligible. (?) However, it seems that the movement of the fluid around the body and through the narrow spaces between the body and the fluid container would be faster (the fluid at "b"). It seems like the change and decrease in pressure on the container from the fluid here would be less likely to be so small as to be negligible here (at "b") if the space is sufficiently narrow. (?) Thank you both for your replies and getting me to think about the different points along the column of fluid and the different changes that perhaps/probably occur. [ Edit: I showed the fluid at "a" moving straight up and i should have showed it swirling around after getting displaced by the falling body. And I might be totally wrong about showing the fluid moving at "c" at all. The fluid below the falling body perhaps gets a bit compressed but it probably doesn't really move until the falling body reaches it and it gets displaced upward around the falling body (which is "b"), right? Apologies. ]

Interesting. Would it be so small as to be negligible? If someone had the right equipment could the decrease in pressure be detected or measured? Thank you.

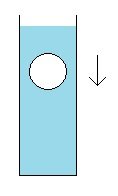
I have found related information but I have not found anywhere on the Internet where this question is directly addressed. A more dense body is falling in a less dense column of fluid. Does the pressure from fluid on the walls of the container decrease? ( My guess is "yes". As the body falls the fluid is displaced upwards and so the fluid moves. ) Thank you : ) [ Edit: I should have said " does the pressure from the fluid on the walls decrease when the body is falling as opposed to before the body falls and the fluid is static ? " ]

Thank you for all of the feedback and replies. I will go and think more about this and about your replies. : ) Thank you and take care : ) !!!

Ah, yes, we are in total agreement. I am sorry. I thought I was clear in my original post, but here is another example of me needing to be clearer. In a tiny tiny little footnote in my original post I buried some important information in the set up. Apologies. Both V's are moving relative to the fluid. Each V is, one, moving relative to the other V, and, each V is, two, moving relative to the fluid. The fluid is in its own inertial frame of reference. And so, in each V's inertial frame of reference the other V will be moving towards the resting V and the fluid will be moving towards the resting V. (In each V's inertial frame of reference the other moving V will be moving faster and in each V's inertial frame of reference the fluid will be moving slower (relative to each V at rest). The moving V length contracts and the moving fluid length contracts (in their direction of motion). The velocity of each moving V will be the same in both inertial frames of reference that the velocity of the fluid will be the same in both inertial frames of reference.) The fact that the fluid moves (and so length contracts in its direction of motion) does not seem affect the analysis of "how is the fluid trapped in the purple inertial frame of reference in the same way that the fluid is trapped in the green inertial frame of reference?". (But, again, the reason why I'm here to to find out if there are parts of this that I am missing, and so I could very well be wrong.) Thank you and I hope this makes things clear (or at least clearer). (?)

Thank you for the reply. I have studies STR to some extent. But I am not expert. However, it is my understanding of STR that "length contraction occurs in the direction of motion" is a very basic concept in STR. If a car is driving down the road at a constant speed and I am standing on the sidewalk, then the length of the car (from the front bumper to the back bumper) will become shorter for me in my sidewalk frame of reference. However, the height of the car (from the bottom of the wheels to the roof of the car) will not length contract in any way and will be the same height for me on the sidewalk as for the person in the car and in the car's inertial frame of reference. And so, based on this understanding of STR, if there are two V shaped bodies moving towards one another (one moving up and the other moving down) then it is my understanding that these V shaped bodies will also length contract in their directions of motion (up or down) and so we end up with the moving V bodies both being obtuse in each other's inertial frame of reference. I apologize. I was sloppy with my language. I was referring to the green-moving-up-V as the "one V" and I was referring to the purple-moving-down-V as the "other V". And I use these two terms ("one" and "other") for the green V ("one") and for the purple V ("other") consistently. However, as you point out, we use the term "other" to mean "the other one". And so, using the language this way, in each V's (green or purple) inertial frame of reference, it is the "other moving V" (purple or green) that is length contracted. And so when I say in my initial post here that in the "other V's" inertial frame of reference (meaning the purple-resting-V) the "one V" (meaning the green-moving-V) I am being confusing and sloppy with my language. Again, apologies. : ) It seems to me (and I may be wrong here) that the two V's will moving towards one another, in both inertial frames of reference, and then collide. And in the green-at-rest V's inertial frame of reference (where the purple V is moving), the first parts of the V's that will collide (given that the green V is a right angle in its own inertial frame of reference and the moving-purple-V length contracts and becomes obtuse) will be the end points of the V's. And in the purple-at-rest V's inertial frame of reference (where the green V is moving), the first parts of the V's that will collide (given that the purple V is a right angle in its own inertial frame of reference and the moving-green-V length contracts and becomes obtuse) will be the angled midpoints of the V's. What happens to the fluid in each inertial frame of reference after the two V's first collide in the two different inertial frames of reference is what I then can't figure out (without ending up in a paradox). Did I misunderstand you? Have I misunderstood any of you? Please let me know. : ) And, thank you all for considering my idea/problem and responding. : ) !

Two V shaped bodies are moving towards one another. One is moving up and the other is moving down. The two V’s are in relative constant linear motion. When two bodies are in relative constant linear motion, the one body could be at rest while the other body is in motion, or the other body could be at rest while the one body is in motion. The moving body length contracts. The moving body length contracts in its direction of motion. In the one inertial frame of reference the other moving V length contracts and becomes obtuse while the one resting V remains a right angle. And in the other inertial frame of reference the one moving V length contracts and becomes obtuse while the other resting V remains a right angle. The V’s are surrounded by a fluid. It is a nearly incompressible fluid. (As the V’s move the fluid is displaced around them. And as the V’s move they collide with the surrounding fluid. And so, for the V’s to remain in constant relative motion with one another there must be another force to offset the deceleration of the V’s due to their collisions with the fluid. (Perhaps there are a bunch of little rocket packs on and along each of the V’s and calibrated just right to keep the two V’s in constant linear motion with each other as they move towards one another while colliding with the surrounding fluid.) The fluid is in its own, third, inertial frame of reference.) In the one inertial frame of reference the first parts of the V’s to collide are the ends of the arms. The collision between the one V body and the other V body is an inelastic collision. When the bodies of the two V's come into contact with one another they stick/fuse together. (It should be noted that the two V’s start out in two different inertial frames of reference but after the collision the V’s are no longer inertial.) And so, after the two ends of the V’s collide and fuse together, this means some of the fluid ends up trapped between the two V’s. There is no way for the fluid to get out from between the two V bodies. (Assume that there is something blocking the fluid from moving “out of the page” or “into the page”.) (Before the two V’s collide, as the openings between their ends get smaller, it gets harder for the fluid to get out from between the two V’s and so even before the two V’s collide they will necessarily start to accelerate and decelerate. No amount of force from the rocket packs will be enough to keep them inertial. (This should be noted. But I don’t think it's important to the overall point/idea here.)) In the other inertial frame of reference the first parts of the V’s to collide are the angled midpoints of the two V’s. The collision between the other V body and the one V body is an inelastic collision. When the bodies of the two V's come into contract with one another they stick/fuse together. (Again, after the collision, or perhaps just prior to the collision, the two V’s will necessarily start to accelerate and decelerate and will no longer be in inertial frames of reference. (And again, noteworthy but perhaps/probably not pivotal.)) And so, in the other inertial frame of reference, after the two angled midpoints of the V’s collide and fuse together, this means the fluid between the two V’s does not end up trapped between the two V’s. There is a way for the fluid to get out from between the two V bodies. And after the two V’s collide and fuse together either at the end points in the one inertial frame of reference or at their angled midpoints in the other inertial frame of reference, the same particles of fluid trapped between the two V’s in the one inertial frame of reference are the same particles of fluid not trapped and are possibly pushed out from between the two V’s in the other inertial frame of reference. If the fluid is pushed out from between the two V’s in the other inertial frame of reference then this is a paradox. How can the fluid between the two V's in the other inertial frame of reference not get pushed out but instead somehow get trapped between the two V's? How can the same particles of fluid and how can the same amount of fluid get trapped between the two V's in the other inertial frame of reference as is trapped between the two V's in the one inertial frame of reference? Thank you for any assistance. : ) --- And a coupla things to note: 1. No body is a perfectly rigid body. But we can assume the bodies of the V’s are much much more rigid (as rigid as theoretically possible) than the body of fluid. 2. When the V’s disturb the fluid, the fluid is then no longer in an inertial frame of reference. Swirling around fluid is not inertial, and displaced fluid is not inertial. (This does not seem to affect the overall logic here, but perhaps it should be noted.) 3. Collisions at “relativistic speeds” (speeds at which the effects of Relativity become noticeable) can end up in explosions and if this happens then where the fluid between the two V’s ends up could then be unknowable. We could say the two V’s here are moving slow relative to one another while the length of their arms are light-years long, and so then explosions are unlikely while the effects of Relativity with these “relativistic distances” are noticeable. Or, we can just stipulate in this thought experiment “no explosions”. “Explosions” are not a necessary element here.

+1 to you too ! 'till later : )

I've been studying Physics on my own, and for the most part this has worked out fine, but every now and then I find myself stumbling into something that I think I understand but it turns out there is a whole bunch of knowledge behind what I'm looking at that I do not have. I appreciate you trying to help me but in reading your response I think this may be one of those times I thought I was playing in the shallow end but I didn't realize I swam out too far. I haven't studied field theory yet and I thought that without knowing a lot about fields I could understand my "electromagnet / permanent magnet " question by staying away from the details of fields and just sticking to the concept of " momentum ". This makes no sense to me. And I'm guessing it's because I don't understand fields and radiation and so on. And so perhaps I need to just tuck away my little question for now and go back and finally get around to studying the basics of field theory. Again, I appreciate you trying to help me, but I think I've swum out too far again on this one. Thank you.

Did you mean to say "You are not correct ..."? I have been saying that the field moves, and if I'm reading you right then I have been wrong to say this. If I'm reading you right then I should have been saying "the EM wave moves" or I should have been saying "the change in the field moves". If I have the terminology correct now, I still think I end up with my same question. Please let me know if I still don't have this ("the EM wave moves") right. But, there is a more basic question I have about the terminology of "+p" and "-p". I thought I understood how you were using it and I thought you made a typo, but now I think I don't understand how you are using these terms. When something moves to the right that is positive momentum and when something moves to the left that is negative momentum (as per convention). And so I thought "+p" means momentum moving to the right and "-p" means momentum moving to the left. When the massive body of the electromagnet moves to the right towards the permanent magnet you use "+p". But when you talk about the EM wave moving towards the permanent magnet, which is also to the right, you use "-p". If this isn't a typo, then I don't understand how you are using these terms/concepts. If you don't mind, could you please explain.

Sorry if my pictures didn't help. When the electromagnet is turned on it accelerates to the right [+p]. But the EM field moving towards the permanent magnet is also moving towards the right [and so it's momentum would also be +p not -p]. However , when the electromagnet is turned on it's field moves both to the left [-p] and to the right towards the permanent magnet [+p]. And I suspect that momentum is balanced in the field between the leftward moving field and rightward moving field itself. When the rightward moving field [+p] collides with the resting permanent magnet [0] I suspect that the field slows down [-p] and the permanent magnet is initially moved to the right [+p] and here momentum would be conserved in this interaction. And then after the permanent magnet is initially moved to the right [+p] due to the collision, the permanent magnet is now in the electromagnet's magnetic field and would then start to accelerate towards the electromagnet to the left [-p] due to magnetic attraction. But, if I'm explained myself clearly enough (and maybe I haven't), and if I'm right (and maybe I'm not), then we end up with momentum being balanced everywhere except for the electromagnet itself accelerating to the right [+p] first and then the permanent magnet accelerating to the left second and later [-p], which would mean overall more rightward [>+p] momentum. This is my problem. If momentum overall is always conserved, which it must be, then somehow and somewhere I've gotten something wrong.

What you say makes perfect sense (and it makes sense with how I understand conservation of momentum). However, the next step in the logic then, I having problems with. If the massive body of the electromagnet begins to accelerate first and then if the massive body of the permanent magnet then begins to accelerate later and second, then we have a momentum imbalance between these two bodies (more positive momentum and less negative momentum). If there is more momentum in the expanding newly created magnetic field around the electromagnet in the leftward direction (more negative momentum) and less momentum in the expanding newly created magnetic field in the rightward direction (less positive momentum) then this imbalance in the field could balance out the imbalance between the two massive bodies. But this doesn't make any sense (and I'm sure you're not suggesting this, i'm just thinking things through out loud). At some point after the electromagnet is turned on ( (distance between them ) / (speed of light) ) its expanding magnetic field, with its momentum, will collide with the permanent magnet. If this collision resulted in the expanding field slowing down (a decrease in positive momentum) while not pushing the permanent magnet rightward (no corresponding increase in positive momentum) then this interaction could result in an overall (massive bodies and fields) balance and so then momentum would be conserved. But, like my previous thinking out loud, this too seems not physically likely. You may have suggested, and you may be thinking, that something different occurs in the rightward moving and expanding magnetic field. As the magnetic field around the electromagnet expands rightward towards the permanent magnet, I can't see (at least not right now) how this field could carry the "information" with it of the electromagnet it is expanding from being in a state of acceleration. Any ideas? ?

So ... is the answer to my question simply that momentum is not always conserved? I assumed that is always was. And, perhaps that is wrong. ?

If the rope has mass then as Bob pulls on the rope the mass of the rope moves towards Bob and Bob moves towards the mass of the rope, and so it seems to me that in this way momentum is conserved between Bob and the rope. And then at some point later Alice is pulled by the moving rope and the pull on the rope by her will slow the moving rope down and accelerate her and then it seems to me that momentum will again be conserved. If the rope is theoretically "massless" what will happen? I don't know. It's an interesting question and it may be a close analogy to what I'm asking here with a turned off and then turned on electromagnet. I don't know. I'll have to think about it. --- (Sorry, I posted this before reading you "second thought".)

I was thinking about the logic of this again. If this force is what leads to momentum being conserved, in some ways it makes sense. If the electromagnet, as its turned on, is further from the permanent magnet then there is less magnetic attraction and if the electromagnet, as its turned on, is closer to the permanent magnet then there is more magnetic attraction. And so if there is a leftward force on the electromagnet as it is turned on, then it would need to be weaker the further the two magnets are apart and it would need to be stronger the closer the two magnets are together, to offset the different amounts of magnetic attraction with different amounts of distance between them. And that the Physics could work out this way makes sense (to me). But then there is also the question of duration. The further the electromagnet is from the permanent magnet the longer it needs to be held in place (as the magnetic field of the electromagnet makes its way to the permanent magnet), and the closer the electromagnet is to the permanent magnet the less time it needs to be held in place (as the magnetic field of the electromagnet makes its way to the permanent magnet), for momentum to be conserved. And this seems more conceptually problematic to me. ? My understanding of the Law of Conservation of Momentum is that it applies to both push and pull. And my understanding of Relativity, and of the Relativity of Simultaneity, is that "events which are simultaneous in one inertial frame of reference are not simultaneous in another inertial frame of reference". If this is correct, this this means by definition Relativity allows for two events at a distance in the one same inertial frame of reference to be simultaneous. My understanding is that the Relativity of Simultaneity applies between inertial frames of reference and not within one single inertial frame of reference. Here, the turned off electromagnet and the permanent magnet are in the one same inertial frame of reference.

Could this force push the electromagnet leftward and balance out the rightward force on the electromagnet (due to magnetic attraction) over the period of time it takes for the expanding magnetic field of the electromagnet to make it to the permanent magnet, so that the electromagnet stays in place until the permanent magnet starts accelerating? If so, then momentum would be conserved (or so it seems to me).

There is momentum in the expanding magnetic field. When the electromagnet is turned on the magnetic field surrounding the electromagnet expands to the left and the right. There is an increase in positive momentum an there is an equal increase in negative momentum. And so, these two momentum increases balance out, and momentum is conserved in this part of the overall system. When the electromagnet is turned on the body the electromagnet begins to accelerate there is an increase in positive momentum in this part of the system. And for momentum to be conserved there must be an equal increase in negative momentum to balance this out. If I understand you correctly, we would only be able to say that momentum is conserved when there is a direct collision between two bodies. I don't think this is how the Law of Conservation of Momentum works. I don't think it is limited in this way.

I'm assuming the electromagnet and the permanent magnet are in the same closed system.