Killtech

Okay, i see a lot of misunderstandings here. I admit what i am suggesting here is so far from the usual of what is done in physics thus is quite natural to happen. But i understand where you are coming from and think we can work it out, if we both try to understand each other. You mention choosing a different connection - and that's what i am doing here. however in GR all such things are done only on a single Riemann manifold, and not between two different ones. This is why you state that we can exchange curvature for torsion and that is correct. In my case i utilize the very same underlying smooth manifold for both geometries (hence coordinates remain the same in both), each is equipped with a different metric tensor. And i do not mean rewritten in different coordinates. L1 and L2 are two disagreeing concept of clocks. I know the concept of coordinate time but this is not what i am referring to. In my case both L1 and L2 are associated each with the temporal part or their own metric tensor g and g' (g_mu,nu != g'_mu_nu in general) - since they represent the proper time of their geometry. For now i left out the discussion of what happens to the remaining complements of the L2 metric tensor - just assume it is constructed suitably. Given a metric tensor, there is a unique torsion free connection associated with it, the Levi-Civita one. We have two metrics, hence two manifolds, hence two LC-connections and each is torsion free on its manifold. On the other hand, since both connections are defined on the same smooth manifold, we can look at the L2 LC-connection from L1 geometry and will notice that it neither won't be torsion free nor more importantly it won't even preserve the L1 metric. The latter renders it quite easy to make c a function of something. I am not sure you are familiar with dealing with such kind of connections. L2 will break the usual parallel transport. It will yield different geodesics. It is entirely a different geometry. Yes, yes i hear all your alarm bells ringing - i know such a thing would normally break all laws of physics. But it is though to be used in accordance to constructing clock and ruler devices that conform to the L2 metric. And if we have both, then it is in fact just like you said, draw different types of maps over the same territory. To stay in your analogy, our maps are good for those that navigate via vision, but for bats that navigate via acoustics, a very different type of map may be needed. Not very revolutionary at all. And sure, so far mathematically this is still kind of trivial, even if it is used in an unfamiliar way. Indeed such a construction appears anything but practical for now. However, we are talking of what would happen if we were to exchange the clocks and rulers we are using in the real world for something else that is not equivalent. I do not mean just using different units. I mean changing such fundamental relations like A longer then B becomes A shorter then B - simple change of units cannot do that. A change of geometry can. Before you object that only one of the statements can be 'real', consider that in math we do often use different metrics or norms on the same space and they will disagree with each other without there being an issue. The reality is that there is more then one way to compare things. The gist of it the definition of the SI second chooses a very specific way to compare time, yet it is by no means a unique choice.

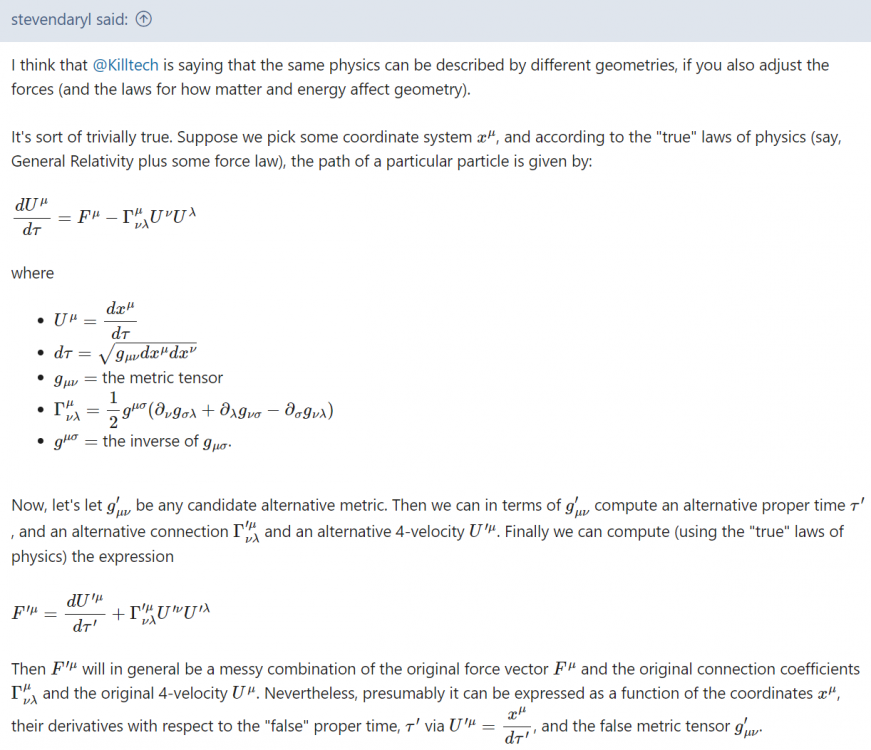
In my case the basis for the change of laws of physics is the consequence of switching between different clocks concepts with which observations and measurements are performed. Thus the change is not physically real, but is a pure result of change of conventions / definitions. Lets consider two particles Pa and Pb modelled in GR with different initial conditions but starting at the same space time location. Lets call this event S. Each particle follows a trajectory dictated by the laws of physics. Lets assume the trajectories are such that they eventually collide. Lets call this event E. Now lets consider two different clocks being placed on each particle, one is the regular SI clock type L1, the other a clock type L2 that corrects for local gravity field. the first clocks describes the regular proper time of GR for each particle, the other clocks provide another proper time which will disagree with the former. Let's assume that the flight time between S and E as measured by L1 clocks shows that Pa needed less time then Pb. Now L2 clocks tick rate will locally differ from L1, specifically let's assume Pb passes through a region where its L1 clock runs slower like a large mass. L2 clocks will adjust for the effect thus lets assume according to L2 clocks Pb needed just as long as Pa. Since L1 and L2 are different measures, there is no contradiction in that observation. In terms of Riemann geometry we can describe the equation of motion for each particle in either L1 or L2 proper time. However, L1 and L2 come with two different (1,3)-Riemann manifolds, metrics, and hence a different connections. These are different geometries. Expressing the very same physics in terms of two different connections will make the same laws of physics look entirely different for each. And they need to be in order to yield the seemingly disagreeing observations of L1 and L2. Yet their predictions, like the resulting trajectories and where they collide will still perfectly agree. This is what the transformation in the quoted post below does

Why would it not be a wave equation? How are Maxwell equations in a medium not wave equations since the speed of light in mediums does vary and is related to the refractive index? How are sound wave equations not wave equations? I fail to understand what you are trying to say. Also i am not transforming between frames. This has nothing to do with coordinates. It is far more fundamental then that. We are transforming between two concepts of proper time. Look at the formula. That is far more involved then a change of coordinates or something as trivial as switching between SI and natural units. Natural units still use the very same definitions of time and space as SI does but just scale them differently with some factors. But a change of proper time is like a local transformation of units. It forces you to rewrite all laws of physics. It changes what is constant and what isn't. Look at the equation and understand how massively it impacts the whole model but not the physics.

you forget an important aspect in your example. While the laws of physics will remain invariant under alterations of the iron-to-iron interatomic distance, the geometry of your space won't be. Lets for example assume the alteration only affects the distance in a local region but not around it. In the case we will measure that this region has a different volume then it would have it it were flat space, no? Therefore the effect is measurable even when using this specific distance definition but realize differently then one might naively think. to make your example more concrete, we can use a simplified temperature model as a factor to alter interatomic distances with the special assumption that our iron ruler always has already taken the environmental temperature before we use it to measure anything (and lets also assume there is no kind of hysteresis effect which would disqualify it from defining a valid distance - as needed for the mathematical definition of a metric space). In this example temperature will change geodesics, i.e. what the shortest path between two points is. Now coincidentally sound waves will follow these geodesics (under ideal assumptions)... therefore the sound wave equation would suddenly become invariant under local changes of temperature.

assume c(x,t), i.e. it may vary by time and region A simple approach for Maxwell with non constant c derived from current physics: SI second definition explicitly states that corrections due to the local gravity field should not be applied. Now define an alternative time measure and clocks with corrections for the local gravity field such as to enable clock in different regions to tick with the same rate. As clocks define the proper time this condition can be translated as to finding a correction such that curvature due to energy-mass vanishes. Defining a new clock and unit of time is so far a change of conventions, therefore does not affect real physics. However it changes measurement (and all SI units depend on the second) and the mathematical model of physics. Now transform maxwell equations from GR proper time tau to new proper time tau' and you get additional time and region dependent terms, one of which describes the wave speed and this we call c(x,t). These new terms reflect the physical degrees of freedom which GR describes via geometry. As a trade-off all physical degrees present in GR are gone, as it now becomes flat by construction. More specifically you do this: in short, the effect of this transformation is that curvature of space time transforms Maxwell into a wave equation in a medium where the medium is just an equivalent representation of what was previously embedded in the geometry. EM-waves represented via tau' now bend in vacuum because it gets a refractive index replacing curvature. it still the same physics, just a different mathematical model that yields the same predictions. To measure alpha, you need to do measurements and all those measurements use SI units, all of which depend on the second. While alpha has no unit itself, it still depends on the geometry of space time and since the definition of the second does define proper time, the geometry is a convention in this context. So no, in SI units alpha can never change, but other units that do not inherently assume c to be constant do allow it to change. You are exactly right, and so far you are the first person i meet that understand this. It however means that the constancy of c is more of a convention of our physical model and specifically our concept of measurement rather than fundamental law of physical. It would also make us free to change that convention, if there was a use case where a different convention would be more beneficial, no?

The constancy of the speed of light is a fundamental assumption in modern physics, built into both relativity and the SI system of measurement. I’ve been wondering: to what extent is this a fundamental property of nature, and to what extent is it a convention tied to our choice of units and measurement definitions? And does our current measurement framework even allow us to establish the possibility of it to vary in the first place? The Issue of Measurement The SI second is defined using atomic clocks based on the frequency of a cesium transition. The meter is defined in terms of the speed of light, which is fixed at 299,792,458 m/s by definition. Since c is numerically fixed, any potential variation in light’s speed would be hidden within changes in how we measure time and space rather than appearing as an explicit difference in measured speed. A Need for a Counterhypothesis To test for a varying c, we’d need a physical framework where such variation makes sense and is not simply reabsorbed into our measurement definitions. But how do we define an operational way to measure a changing c, when our time and length units are already tied to its assumed constancy? The Variation of c The fine-structure constant alpha is given by: e² / (4pi epsilon0 hbar c), meaning that if c varied, so would the constant. Since the energy levels of Caesium atoms - and thus atomic clock frequencies - depend on alpha, any variation in c would affect the very clocks we use to define the second. This creates a self-referential issue: if we use atomic clocks to measure changes in c, but those clocks themselves change due to variations in c, can we even establish whether c is varying in the first place? If c depended on location, it would cause clocks in different regions to tick at different rates. Since clocks define proper time, this effectively means that a variation in c would manifest as spacetime curvature. How, then, would we distinguish such an effect from gravitational time dilation caused by mass-energy? Back around 1900, Poincaré already recognized the subtleties in these assumptions and criticized how astronomers arrived at their conclusion that c was constant. In modern physics this consideration is even more interesting to explore. I tried this conversation with ChatGPT, and it was well versed to discuss the topic. Here is a link to that conversation: link deleted; violation of 2.13 I’d love to hear thoughts on whether this is a meaningful issue to explore.

Mass is a thing of reality, while energy is an abstract concept of our description of nature, that reality does not need to care about. the concept of energy arises conservation laws which are a consequence of symmetries, which again are arise from how we define time and space relative to natures laws. different definitions of the latter lead to different deductions of the former. Einsteins relativistic notion of space time (specifically his clocks) leads to the relation you mentioned, but if you were to use an absolute space time defined by a coordinate time and space and took the symmetries it is subject to, you get a coordinate energy unit with different relations. energy is an extremely useful tool for the calculus, but it is not real in the same sense as mass, space, time or change, which all come with their own unique units expanding the degrees of freedom of the universe, while the deducted quantities like energy, (angular) momentum all have units assembled from those fundamental ones and describe the constrains of the world.

F is a function of coordinates x and t, i.e. F(x,t) whereas F' is a function of coordinates x',t' i.e. F'(x',t') please look up how a change of variables works in math: https://en.wikipedia.org/wiki/Change_of_variables_(PDE) . the wiki article on Galilean invariance also explains it for the specific case of Galilean transformation. i really recommend you to read and understand it first. what you have written is a mixed picture using functions of old and new coordinates. you did not correctly/fully exchanged the variables.

lets take a combination of a uniform motion plus a translation like x′=x+vt+x0 t′=t+t0 then \(\frac{dx'}{dt'}=\frac{dx}{dt}+v\) and \(\frac{d^{2}x'}{dt'^{2}}=\frac{d^{2}x}{dt^{2}}\) therefore \(F'=m\frac{d^{2}x'}{dt'^{2}}\) you can go through the other elements of the Galilei group and check it remails invariant. EDIT: shouldn't have bother to write it down myself. here you have it on wikipedia, the Galiean relativity . also latex \frac breaks on editing

coordinates are needed to under the hood almost everywhere in physics. this is because in order to define differentials they are the minimum requirement. and even the coordinate free formulation of equations in geometry isn't entirely free of coordinates, because it still requires smooth manifolds to define them which in turn use atlases of coordinate maps for their definition. i am not sure i understand what you are trying to imply here. there is absolutely no physical phenomenon which depends in any way on your choice of coordinates. there cannot be, coordinates only affect the calculus and are entirely independent of physical predictions. the only thing that depends on the choice of coordinates is the length of your calculation needed to make a prediction - the result does not. Look up the Noether theorem. it's pretty standard. Specifically look up how (classical) energy conservation is derived in classical mechanics. the translation symmetry is needed to deduct the momentum conservation, while rotation symmetry gives you conservation of angular momentum. i hope you do not question those in classical mechanics? Show me what your textbooks says, so we can clear up the misunderstanding.

what you refer to is the geometric formulation using the metric. i covered that in the response above and saw no need to repeat. Classical mechanics are invariant to translations, uniform motion and rotations, the Galilean group. Noether uses that to deduct the corresponding conservation these invariances imply.

Yes, sort of. I am trying to understand how a geometric representation works to modelling the medium of a wave equation - as if the medium *was* the underlying spacetime. The idea is to make the math as close as possible to electrodynamics in GR (not the actual physics. that won't change) and find a corresponding interpretation (artificial clocks and rod). When i could achieve that, i would be able to do the reverse for electrodynamics, i.e. find a generalized Lorentz Aether formulation for gravity that however remains equivalent to GR (still boring, still no new physics. though it might be interesting for quantization of gravity). So far that's only a pure math exercise. Now the actually interesting part: comparing the two i am interested in the special behaviors sound wave can show that light does not: sound in a vortex, i.e. the situation of the medium flowing in a curl. as far i am aware spacetime in GR cannot do that. The question behind it is if extending GR with such new (yet analog) physics could resolve the galaxy rotation curve discrepancy and therefore remove the need for the vast majority of dark matter in the universe. The issue: the road there is long and i have to start small... and even the small part turns out hard enough to discuss. That is the only claim i used. you do not need anything more that an equation in a single frame and its coordinates to evaluate the structure and invariances of it. all coordinates are defined relative to that one base frame/coordinates where the equation holds. if you change coordinates only, you do not automatically change the frame. energies and momentum stay as they were in the base frame (as in you have to rewrite energy in the base frame according to the new coordinates). I have made the mistake of taking that for granted, and probably made the mistake myself that i may have called a change of coordinates a change of frames, which are two different things. it takes a change of the metric (geometry) to do more - which requires the introduction of artificial acoustic clocks and rods. those new clocks and rods would then be needed for all measurements to ensure experiments still agree with the model. i realized that adding that step would confuse people even more so i tried to constrained the discussion to coordinates only after the initial posts. One way or another, you do need nothing more then a quite weak physical postulate (wave equation in one frame) and the coordinate invariance follows. This is of course only half way to constructing something like a relativity principle analog for sound.

ah, i am more clearly understand your point, but i fear there is still a misunderstanding i need to clean up first. as a person with a stronger math background, i feel particularly unqualified to make my own physical postulates and instead prefer to start working only with what i am given. this constrains me to do only the most boring well known physics (and technically this subforum too, since everything else would go into speculations?), but there is still quite a few things in the math framework that still allow to get maybe a novel perspective. unlike relativity, i haven't deliberately made a alternative formulation of the relativity principle for sound. i only claim that in my particular scenario the exist one frame such that the well know acoustic wave equation holds. the invariances of that equation are implied by that singular postulate in that frame and math - but they do not really mean much. a coordinate can be anything weird like a angle. a coordinate transform like x→2x does not suddenly halve the length of rods. Europe doesn't become smaller then USA in area just because you transform from feet to meters - the difference is merely in numbers, not reality. so if there are just coordinates, that make the equation looks the same, it is at first a mathematical trickery that has no actual impact on physics whatsoever. and in fact, outside of acoustics itself, in those coordinates not much else of the real world will be (acoustically) Lorentz invariant. instead one has to do some artificial constructions to find anything that is, like i tried here (look for the picture): https://www.scienceforums.net/topic/132777-analogies-for-relativistic-physics/?do=findComment&comment=1254430. the seemingly much lower speed limit is merely a coordinate illusion in the case of acoustics. Except for one thing: an acoustic wave carries energy and momentum and can interact with other objects, yet its physics limit it such that there is no possibility of it accelerating anything past the speed of sound. it may be a boring math exercise to use such an illusive framework to still arrive at the same old predictions we have for sound, but it is nevertheless noteworthy that one can make it work (accounting that a real rod is acoustically Lorentz variant). the one thing pointed out by this, is how such a relativity is strictly applies only to all the things directly related to the equation it originates from. Now if we compare that to electromagnetism, what else is there actually in reality that isn't electromagnetic? is there even a singe weak or strong interaction that does not involve neither light nor charge? And since a real solid state rod is shaped by the electromagnetic force, it has to comply with its invariances, rendering the math of it a reality rather then an illusion of numbers. This seems to be the crucial difference between sound and light. Then again, considering that the standard model faces some challenges with its predictions, like the muon anomaly or the proton size in muonic atoms, it isn't actually entirely clear to me if we do have enough evidence to fully rule out Lorentz violations by these forces (e.g. what if the muon interaction would have a minor frame dependence?).

oh, okay this was merely a sidenote i made as an interesting curiosity. i think you mean this: i fear the bold text may have gone under the bus in our conversation. But also i am well aware there isn't a preferred frame in general, particularly in a infinite flat Minkowski space. i am sorry if you got the impression i suggested otherwise, but i am not sure what better words i should have chosen instead. This was the original starting point i meant on this part of a conversation: Again, the bold text highlights this procedure is not possible in the normal case of SR. the inability of direct comparisons between inertial frames allows the relativity principle to not just hold locally, but even apply globally. i have to admit that when i learned about SR, i had some trouble how to interpret time dilation in relativity, whether it was a "real" effect or just a mathematical artifact of the specific representation. So this lead me to look for ways to achieve a direct comparison between inertial frames and figured that such a setup might do the trick. found out there are already papers handling it. while this case is by no means applicable in general, it still helps to build an interpretation, and particularly point out that relativistic effects cannot be considered mere artifacts. Furthermore it is interesting to study this in context to what it actually means for how we define length and time.

The question was, what would happen if we could meaningfully compare the length of a meter and that of a second in between inertial frames.

Is it a neccessary condition? Actually, aren't some big bang models of the universe compact (honestly i don't know)? what you need for comparisons are geodesics that repeatedly meet.

English isn't my native language, so please help me understand how that only quote of yours in this thread implies there is more then one Lorentz group? I have to admit i still cannot find an interpretation of it that would conform with what you just said. Or was one of your responses maybe deleted? Also where did you get the impression that i mixed up the Lorentz groups? i have tried to point out quite a lot that this is an analogy, i.e. not the same thing, and i tried to stress that out a lot by prefixing the concepts with the word "analog" to make it apparent it is not the same as in relativity, but rather a mathematical analog with the constant replaced by another.

If you cared to read the conversation you were responding to, you would know you don't add anything already said. But if you put it that way, the "general" case does not apply so generally, if there are counterexamples against it. note that the compact space case is just the easiest example to illustrate the issue, so do not make the fallacy to assume its a necessary a condition. oh, sorry it didn't cross my mind that anyone on these forums wouldn't know these, so i didn't understand your question. Yeah, you misread the original post so much, i didn't even bother to try to correct you. But fair enough, especially for physicists, i suppose it is very easy to forget that there is not just one Lorentz group since only the one specific to the speed of light is used in physics. You forgot that if you take the Lorentz group and replace c by any other constant, you get another group with identical structure - and it is also still commonly referred to Loretz group, because in math c play no special role. However, the group acts quite differently on the space, and in particular combining elements of different Lorentz groups end up being elements of neither. So in this case this creates a little ambiguity and i guess i cannot entirely blame someone for stopping reading at "sound wave equation is Lorentz-invariant" and therefore missing out that a different Lorentz group was meant, which should have become clearer when reading further. Since you mentioned the d'Alembert operator, lets go back to the linear acoustic wave equation and notice how we are talking about the same structure - where only the constant is a different one. One could just write \(\Box p=0\) instead but that would omit the material specific propagation constant within, which just fuels the confusion you fell for. But since i apparently do not understand the concepts of relativity, would you please be so kind to enlighten me and the other people in the conversation on the invariances of the d'Alembert operator (or any other operator with the identical structure) and name the 3 subgroups of transformations of the Poincaré group it is invariant under?

it's this one here: https://en.wikipedia.org/wiki/Acoustic_wave_equation#/media/File:Derivation_of_acoustic_wave_equation.png the time derivative is also 2nd order but one character is missing. without a preview function i had some trouble with the latex. As one can easily see the solutions to that equation are normal travelling waves. remember you posted a more general book on the topic and you can find the equation in your link as well (https://www.scienceforums.net/topic/132856-wave-equation-in-a-medium-with-smooth-nx-refractive-index/#comment-1253798) where travelling waves are studied. i am not sure i understand that remark on wiki mentioning the standing wavefield. Here is also the slightly more general case used for traveling waves in a medium with refractive index of which this isa special case: https://wiki.seg.org/wiki/The_eikonal_equation Indeed the topology discussed in that paper is hypothetical since we never observed the universe to have a limited expanse in any direction so far. However, it that were the case, the existence of preferred frame is a consequence. The issue is that the finite expanse does not allow for the relativity principle to hold globally. the interesting thing about that scenario is that the inertial frames are no longer perfectly equivalent and can be distinguished. in other words the relativity principle cannot not hold globally any longer and instead it defines an unique preferred inertial frame. That is the crux of the matter and it is discussed there e.g. here: https://arxiv.org/abs/gr-qc/0101014 you can find other papers on the topic since it is a known case. the wiki article has a section about the special meaning of the preferred frame in aether theories and that is the meaning here as well.

https://en.wikipedia.org/wiki/Preferred_frame that's the meaning and that is the case in that special topology.

I made that typo in my original post, and i corrected it in the repost. the value i used for \(\gamma_s^2\) is correct though and the calculation that follows is too. thanks for finally reading it. No, this is different. Each person has the means to determine if it is in the preferred frame or not. Locally the preferred frame changes nothing, so you cannot detect it by local means if your frame is in fact the preferred one or not. Only globally it makes a difference. it is different then in regular case of SR where the global detection isn't possible.

sorry, i have to correct you there. a change of coordinates does not in any way change the original equation, but merely chooses a different representation of it. there is a clearly defined method how a change of variable must be performed exactly, so it has no effect on the predictions being made. The form of the equation after a coordinate transformation is derived from know facts, not assumed. I have calculated a prediction using two ways, one using the straight forward calculation using most basic knowledge and only the other makes use of the A'rentz invariance. you then have to explain to me how it is possible that the result is the same, regardless of the method - with or without the use of invariance.

Normally there isn't but if you read the paper, you will find that SR in that scenario has a preferred frame. there are enough reviewed papers on this, if you don't believe me. Yes, i meant there is one frame where one ages more rapid, more rapid then in any other inertial frame, i.e. that frame becomes uniquely special by that property and is hence considered the preferred frame.

Of course. I haven't made any physicals assumption apart from the well established acoustic wave equation in the case of a stationary medium. Everything else in that post is merely a consequence of that. Know what? i repost it... Let's start with the linear approximated acoustic wave equation \(\partial_{x}^{2}p-c_{s}^{-2}\partial_{t}^{2}p=0\) in the case of a stationary medium, where \(c_{s}=\frac{1}{3}\frac{km}{s}\) is the speed of sound in the medium we use. This is of course the version with only one spatial dimension, but for the simplicity it is enough for now. The equation should hold in the rest frame of the sonic medium. Let's compare this model with the historic start of SR, when light in vacuum was still modelled as traveling through a luminoferious aether medium. Apart from having an equation for a longitudinal wave instead of a transversal one, the models are very similar. And indeed a wave in a medium was what inspired Lorentz approach. However, the peeps of old found out quickly, that these type of equations are invariant under a special type of coordinate transformation, the Lorentz trafo. Coordinates are just a math tool and have not much to do with physics per se, so let's ask the question we can play an analogue trick for acoustics and in fact a trafo like \(t'=\gamma_{S}(t-vc_{s}^{-2}x)\) and \(x'=\gamma(x-vt)\) with \(\gamma_{s}^{-2}=(1-\beta_{s}^{2})\) and \(\beta_{s}=vc_{s}^{-1}\) - (note that here \(c_{s}\) is the speed of sound!!) transforms the wave equation into \(\partial_{x'}^{2}p(x',t')-c_{s}^{-2}\partial_{t'}^{2}p(x',t')=0\), i.e. sound remains invariant under these kind of coordinate changes. In order to give a little more life to this math curiosity, let's consider @studiot simple experiment where we have one observer and a wall on the ground 1km away from each other. The observer emits a sound wave, it is reflected by the wall and an echo returns to the observer. The time is measured how long it takes to go there and back again... not the hobbit, just his sound. This setup will be discussed under two situations, in calm weather with no wind speed and in windy conditions with a speed of \(v=\frac{1}{5}\frac{km}{s}\). For reference, let's do it classically first, that is in calm weather it takes sound \(\Delta t=c_{s}^{-1}\cdot(1km+1km)=6s\) to get back. When there is wind it's \(\Delta t=(c_{s}+v)^{-1}1km+(c_{s}-v)^{-1}1km=(\frac{15}{8}+\frac{15}{2})s=\frac{15+60}{8}=9.375s\) Now let's do the wind case differently. Exploiting the A'rentz invariance of sound, we can start in the wind frame (rest frame of the medium) where we have the wave equation for and just transform to the ground/observer frame, right? For that we get \(\beta_{s}=vc_{s}^{-1}=\frac{3}{5}\) and \(\gamma^{-2}=(1-\frac{9}{25})=\frac{16}{\text{25}}\), thus \(\gamma_{s}=\frac{5}{4}\). Appling that ensures the equation keeps its form same as in the calm weather case. Unfortunately, there is a bit more to do, because if the distance between observer and wall in the wind frame was \(\Delta x=1km\) and moving with \(v\), then in the new coordiantes it will undo an A'rentz length contraction back into its rest frame and therefore \(\Delta x'=1\cdot\gamma_{s}=\frac{5}{4}\) and hence the signal will need a travel time of \(\Delta t'=2\Delta x'c_{s}^{-1}\). However, notice that it is given in the coordinate time \(t'\) and not \(t\) and therefore we have to transform it back, so \(\Delta t=\gamma_{s}\Delta\,t'=2\gamma_{s}^{2}c_{s}^{-1}=\frac{2\cdot25\cdot3}{16}=\frac{75}{8}=9.375s\) Either framework produces the exact same prediction for this well know acoustic situation, with the former being known to agree with reality/experiment.

of course i do. In this particular scenario it is possible to find a preferred frame and it is where people age the most and the circumference is minimal. We can further analyse the frames with a Sagnac detector: send light around the circumference of the torus in both directions at the same time and measure if there is a delay between the in the arriving light signals. In this special topoligy we can use the result to measure the one way speed of light. The preferred frame is a frame where the Sagnac test yields no delay while all other will have one. If we compare what happens in the same situation with acoustic signals in a Sagnac detector, we will find the exact same result. The preferred frame is the rest frame of the medium while inertial frames that measure delay in the arriving light effectively measure the wind speed.