Everything posted by Whitefoot
-
I have some numerical findings about electrons that I think are new:
The first page of my paper shows the compatibility of the ratios of electron radii with the ratios found in the geometry of a self-intersecting torus. This only shows the conceivability of a possible connection. I'm not able to make experimental predictions from what is only the beginning of a proposed model. I haven't been able to take it farther than what I currently have. I am adding the first page of my paper here again for readers who probably aren't familiar with it: Click to enlarge. Note that when the electron radii are used, the self-intersection of the torus will be tiny. It is shown large here for illustration.
-
I have some numerical findings about electrons that I think are new:
But it wouldn't be a toroidal helix compatible with lengths related to the electron. The ratios Rclassical/Rcompton = Rcompton/Rbohr = alpha suggest this specific geometry.
-
I have some numerical findings about electrons that I think are new:
Yes, I've defined them to show the possible fit to the geometry of a self-intersecting toroidal helix.
-
I have some numerical findings about electrons that I think are new:
Looking back over the posts, I don't think I adequately responded to this. Excerpted from my paper page 2: The 2nd and 3rd lines show that beta and gamma of my model are tied to the Compton radius and the fine structure constant alpha, both physical constants. The Compton radius is more commonly called the reduced Compton wavelength.
-
I have some numerical findings about electrons that I think are new:
I haven't been able to solve that. Maybe interacting with the Higgs field would lead to an optimal orbit. From Wikipedia: "The Higgs field is a field of energy that is thought to exist in every region of the universe. The field is accompanied by a fundamental particle known as the Higgs boson, which is used by the field to continuously interact with other particles, such as the electron. Particles that interact with the field are "given" mass..." Given the two chiralities possible for a toroidal helix, I think the geometry is a natural fit with the existence of matter and anti-matter. I know toroidal models have been attempted for a long time, but I haven't seen this particular geometry described before. Suggesting a geometry is probably about as far as I will be able to go with the model with my limited knowledge of physics.
-
I have some numerical findings about electrons that I think are new:
Page 1 of the paper shows RI/RC equal to RC/RB equal to the fine structure constant alpha. That is (Classical radius)/(Compton radius) equals (Compton radius/Bohr radius) equals the fine structure constant alpha. This is well established physics - ancient in fact. I didn't work thru the algebra, but the calculations for beta and gamma are shown on page 2. The diagram of Fig 1 shows that (beta-gamma)/Rc equals Rc/(beta+gamma) for a self-intersecting torus. The matching ratios: (Classical radius)/(Compton radius) equals (Compton radius/Bohr radius) (beta-gamma)/Rc equals Rc/(beta+gamma) suggest that the lengths associated with the electron can conceivably fit the geometry of a self-intersecting circular toroidal helix. I haven't seen this proposed in other toroidal models. I am assuming even free electrons have these orbits - that somehow it is a stable geometry. I don't know if the radii change, since I don't have numerical results to back this up, and I don't have results that would apply to other atomic orbitals. I haven't been able to go beyond what is in my paper and what we have discussed in this thread. From a previous post: Since the calculated radius of this object is quite small, 2.035E-19 meter, for now I'm calling it the quantum rather than make up some new terminology. I'm just not inclined to make up new words. That number refers to the radius of an object treated as a sphere in the calculations. I haven't yet been able to solve for speeds and resulting mass. That's the main direction I've tried to go with this. My paper was focused on the electron and I wasn't even thinking about atoms at the time.
-
I have some numerical findings about electrons that I think are new:
Going back a ways, I can improve my answer. At first I said: My section in diagram 1 of the paper may give an erroneous appearance, but the lengths there are greatly exaggerated for illustration. I'm now adding: Since gamma is the length from the center of the circle to the center of the torus, the section in Fig 2 shows that beta+gamma is almost equal to twice beta, but not quite, when using values for the electron. I think this is where you may get the impression that it is twice the correct value, but within the model beta+gamma still corresponds to the Bohr radius. From the model, beta-gamma equals the classical radius, which is a very small difference. That's beta minus gamma.
-
I have some numerical findings about electrons that I think are new:
Within the context of my model, beta plus gamma, terms that I have defined, correspond to the Bohr radius. Is this a semantics complaint? I'm not able to answer your question. I haven't even been able yet to figure out how charge arises from the model. I haven't even been able to account for spin or other known electron properties.
-
I have some numerical findings about electrons that I think are new:
My model shows that the Bohr radius is equal to beta plus gamma. In the model, gamma is the length from the center of the toroidal space to the center of the circle defining the toroidal space. Beta is the radius of the circle. Beta plus gamma, the Bohr radius, gives the length from the center of the toroidal space to the outermost radius of the toroidal space. For an atom, with the nucleus at the center of the toroidal space, the outermost radius of the electron orbit is at a length of one Bohr radius. My section in diagram 1 of the paper may give an erroneous appearance, but the lengths there are greatly exaggerated for illustration. Since the calculated radius of this object is quite small, 2.035E-19 meter, for now I'm calling it the quantum rather than make up some new terminology. Orbiting in space. I'm only connecting the lengths associated with an electron with a possible geometry. I'm not able to explain all of physics yet. Since a toroidal helix can have one of two chiralities, toroidal models can fit with the existence of matter and antimatter.
-
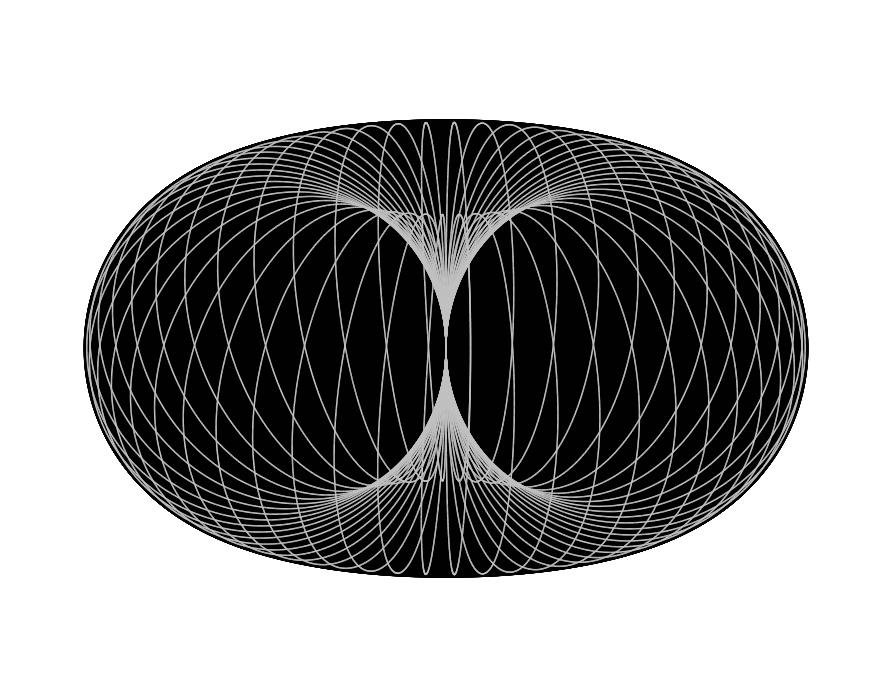
I have some numerical findings about electrons that I think are new:
Some questions by studiot made it clear I need to better describe my electron model. This is to elaborate a bit on my post. This material is not in my paper. The proposed electron is comprised of a quantum traversing an orbit that is a self-intersecting circular toroidal helix. The electron orbit has an outermost radius equal to the Bohr radius. The electron classical radius is roughly 13850 times larger than the moving quantum proposed to make up the electron. The proposed electron then is mostly empty space. The electron classical radius gives half the width of the intersection at the center of the electron orbit. It is well established that hydrogen nuclei are smaller than the electron classical radius. In an atom, the nucleus would be at the center of electrons as modelled here. The first figure roughly illustrates the electron orbit with the gray helical curve. The pitch of the helix, analogous to a thread pitch, is not yet determined in my paper. The intersection at the center of the toroidal space is way too small to show up in this figure. The second figure is only included to give a bit of perspective on the first figure.
-
I have some numerical findings about electrons that I think are new:
I haven't agreed that the first page is flawed. I may have used the word 'radius' when the word 'length' is maybe more appropriate, but that's kind of moot. The lengths associated with the electron have been traditionally referred to as radii, with the possible exception of what I call the Compton radius. There are probably flaws there, not to imply that they are totally flawed. I have agreed that a change of units would invalidate the numerical matches I found. Not very soon - sorting out problems in the last 3 pages is not a simple thing. I don't think the first 2 pages need redoing. This part of the paper is simply showing how 3 lengths associated with the electron can also be associated with the geometry of a self-intersecting circular torus. There are no subtle problems with unit changes and there is no conflict with known science, since there is not yet an established physical model of the electron. From the later part of the paper, I am suggesting the electron is comprised of some much smaller quantum, traversing a circular helical curve that wraps around a toroidal surface. The torus is not physical, it defines the shape of the geometry. The electron then is mostly empty space. In an atom, the nucleus would be at the center of such electrons, and therefore the Bohr radius comes out just right. I didn't develop these added details in the paper. Thanks for the PDF. I have seen some of the toroidal models. I haven't seen any that identify the 3 electron lengths with a self-intersecting circular toroidal geometry as I've done here.
-
I have some numerical findings about electrons that I think are new:
A PDF of my 5 page paper is attached to the fifth post in this thread. As nearly as I can tell, it is only downloadable if you are signed in. As this thread has established, and I agree, calculations on the last 3 pages are flawed.
-
I have some numerical findings about electrons that I think are new:
I'm posting here the diagrams that I neglected to post earlier (essentially the first two pages of my paper). I think the proposed electron geometry may be of interest, despite my further calculations looking flawed. The duplicated values are just a numerical check.
-
I have some numerical findings about electrons that I think are new:
I assumed that pointing out the diagram was a representation of a 3D object answered the question. As to the symmetry of a torus versus a sphere, I don't know if this affects the validity of the model or not.
-
I have some numerical findings about electrons that I think are new:
From swansont's suggestions, and some recalculations, I now agree that a change of units invalidates the numerical matches. The recalculations suggest I'm not likely to fix the problem very soon. Thanks everybody for the feedback. I addressed this in a previous post: The diagram on the first page is a 2D representation of a cross-section of a 3D self-intersecting torus. The intersection is shown large to illustrate how three lengths, analogous to the three electron radii, can be seen as part of the geometry of a self-intersecting torus. The discussion in the paper analyzes this better than I can do by repeating it here. The second diagram in the paper is also a 2D representation of a cross-section of a 3D self-intersecting torus, with a tiny intersection. This is roughly drawn to scale when the three electron radii are used in the torus geometry. The diagrams also show that there are actually two radii that define the torus, and combinations of them make up the electron radii. The Compton radius is more typically called the reduced Compton wavelength, or Compton length.
-
I have some numerical findings about electrons that I think are new:
I have followed the arguments that a change of units will negate the numerical matches I'm finding. swansont has given me some ideas I can use to take a closer look at my model. In order to test it for a change of units, I have to know how the various constants depend on a change of units. His comments have steered me mainly to Wikipedia to learn more about the physical constants, and now I have something to actually work with. The use of math for numerical evaluation is integral to science.
-
I have some numerical findings about electrons that I think are new:
I've been paying attention to swansont's input - he's giving me something I can work with. I'm not ready to just accept someone telling me it's a hopeless cause.
-
I have some numerical findings about electrons that I think are new:
From another Wikipedia page: The magnitude of the kelvin was redefined in 2019 in relation to the physical property underlying thermodynamic temperature: the kinetic energy of atomic free particle motion. The redefinition fixed the Boltzmann constant at precisely 1.380649×10−23 joules per kelvin (J/K). This suggests that there might be a dependence on time units for the kelvin. Since the Boltzmann constant is now fixed, maybe it has no influence from time units. I'm going to be trying calculations with or without a factor of 60 in various places and see what happens. Thanks for the discussion - this gives me a new aspect to look at in the model.
-
I have some numerical findings about electrons that I think are new:
The redefinition bases the constant on an energy equivalent - introducing a dependence on time units, I think. I've almost come around to agreeing that the numerical match won't hold up with a change of units. But I'm going to try some calculations with factors of 60 to see what happens. I'm referring to the redefinition of the kelvin. I've already seen this since they define the size of the Compton radius, which supports your argument that the numerical match won't hold up. I plan to do more calculating anyway and see what results.
-
I have some numerical findings about electrons that I think are new:
I expressed myself wrong. I meant to say inconsistent units. I am looking at a recalculation based on minutes, but this is not straight forward since time units enter into the Boltzmann constant, the Planck constant and the mass of the electron. And apparently the kelvin. Since 2019 the kelvin definition has been based on the energy equivalent as given by Boltzmann's equation. From Wikipedia.
-
I have some numerical findings about electrons that I think are new:
That probably won't happen today. I can see that a change from seconds to minutes obviously changes the value of the Boltzmann constant. I think that base units of seconds are more consistent with the way these units and values have developed.
-
I have some numerical findings about electrons that I think are new:
The units in a calculation have to be consistent to get meaningful results. Within my calculations, using consistent units makes accidental numerical matches fairly improbable. I can see no obvious reason why the numerical matches wouldn't hold up with a consistent change of units.
-
I have some numerical findings about electrons that I think are new:
1. The units aren't arbitrary. I made the proper conversion into base units for the Boltzmann constant. That way the units in my paper are consistent. 2. From CERN: "In the first moments after the Big Bang, the universe was extremely hot and dense. As the universe cooled, conditions became just right to give rise to the building blocks of matter – the quarks and electrons.... It took 380,000 years for electrons to be trapped in orbits around nuclei, forming the first atoms." It may have taken 380,000 years because the electrons were initially in a highly expanded state due to the high temperatures. Since my model is not far enough advanced yet, I can't make any useful numerical arguments related to the early universe. 3. See nr 1. The numerical matches seem like a highly improbable accident.
-
I have some numerical findings about electrons that I think are new:
I am using units consistently in my calculations. pV = NkT would not hold if the various values were expressed in different units.
-
I have some numerical findings about electrons that I think are new:
I know I haven't made the connection between units, but the accurate numerical match seems like more than coincidence. The match applies when the Boltzmann constant is expressed in base units of meters, grams and seconds. The electron surface area is expressed in square meters. From Wikipedia: "Immediately after the Big Bang, the universe was a hot, dense plasma of photons, leptons, and quarks..." This is not incompatible with the model. Large electrons with toroidal forms dependent on temperature could easily be present in a hot, dense plasma. I'm not assigning numbers to letters of the alphabet and trying to decipher the Mark of the Beast.