KJW
Senior Members-
Posts
486 -
Joined
-
Last visited
-
Days Won
3
Content Type
Profiles
Forums
Events
Everything posted by KJW
-
It could be that the earth's crust has already been depleted of its sodium by all the rainfall.
-

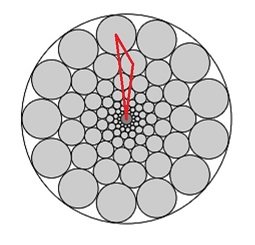
Proportion of the area covered by circles
KJW replied to Dhamnekar Win,odd's topic in Applied Mathematics
[math]1 + \alpha = \dfrac{(4 - \phi^2) - \sqrt{12 \phi^2 - 3 \phi^4}}{2 (1 - \phi^2)}[/math] From here, I took a shortcut and simply ignored the two [math]\phi^2[/math] outside the square root and the [math]3 \phi^4[/math] under the square root because I could see that these are not going to be a part of the final result. Thus: [math]1 + \alpha = \dfrac{4 - \sqrt{12 \phi^2}}{2}[/math] for [math]x \to 0[/math] (ignoring higher-order terms) [math]1 + \alpha = 2 - \sqrt{3} \phi[/math] However, one can verify that the shortcut leads to the same result as follows: [math]1 + \alpha = \dfrac{(4 - \phi^2) - \sqrt{12 \phi^2 - 3 \phi^4}}{2 (1 - \phi^2)}[/math] [math]1 + \alpha = \dfrac{(4 - \phi^2) - \sqrt{12} \phi \sqrt{1 - \dfrac{1}{4} \phi^2}}{2 (1 - \phi^2)}[/math] The series expansion of [math]\dfrac{1}{1 + x}[/math] and [math]\sqrt{1 + x}[/math]: [math]\dfrac{1}{1 + x} = 1 - x + x^2 - x^3 + \cdots = 1 - x[/math] for [math]x \to 0[/math] (ignoring higher-order terms) [math]\sqrt{1 + x} = 1 + \dfrac{1}{2} x - \dfrac{1}{8} x^2 + \dfrac{1}{16} x^3 - \dfrac{5}{128} x^4 + \cdots = 1 + \dfrac{1}{2} x[/math] for [math]x \to 0[/math] (ignoring higher-order terms) Thus: [math]\dfrac{1}{1 - \phi^2} = 1 + \phi^2[/math] for [math]x \to 0[/math] (ignoring higher-order terms) [math]\sqrt{1 - \dfrac{1}{4} \phi^2} = 1 - \dfrac{1}{8} \phi^2[/math] for [math]x \to 0[/math] (ignoring higher-order terms) [math]1 + \alpha = \dfrac{1}{2} (4 - \phi^2) (1 + \phi^2) - \sqrt{3} \phi (1 - \dfrac{1}{8} \phi^2) (1 + \phi^2)[/math] [math]1 + \alpha = \dfrac{1}{2} (4 + 3 \phi^2 - \phi^4) - \sqrt{3} \phi (1 + \dfrac{7}{8} \phi^2 - \dfrac{1}{8} \phi^4)[/math] [math]1 + \alpha = 2 - \sqrt{3} \phi + \dfrac{3}{2} \phi^2 - \dfrac{7 \sqrt{3}}{8} \phi^3 - \dfrac{1}{2} \phi^4 + \dfrac{\sqrt{3}}{8} \phi^5[/math] [math]1 + \alpha = 2 - \sqrt{3} \phi[/math] for [math]x \to 0[/math] (ignoring higher-order terms) -

problem with cantor diagonal argument
KJW replied to phyti's topic in Linear Algebra and Group Theory
More like, make up your mind, which is it. I actually said: "E0 must be a member of L". I didn't say that E0 is not a member of L. You incorrectly inferred that from: "When the sequences are placed into a list, the diagonal argument shows that although the negation of the diagonal belongs to the set of sequences, it does not belong to the list of sequences". E0 is a member of the set of sequences. E0 is not a member of the list of sequences. This is not a contradiction. The list of sequences is not the set of sequences. Cantor proved that the list of sequences is not the set of sequences. You are not going to convince me otherwise. The infinite binary tree is actually ambiguous. It can represent all possible sequences of 0 and 1, or it can represent all possible finite sequences of 0 and 1, which is still infinite. The latter can actually be made into a list. The former cannot be made into a list. Your argument becomes invalid if you assume the binary tree represents all possible sequences of 0 and 1 but treat it like it represents all possible finite sequences of 0 and 1. Due to the subtlety of the distinction between these two cases, I will not accept an argument from you based on a binary tree and will assert that a binary tree is not a list. That Cantor can define an E0 that is excluded from the list is what proves his theorem. I suspect that you think he has forced a result. It is true that regardless of how a list is constructed, even if it is formed from a set that can be listed, the E0 derived from this list will be excluded from the list. But E0 isn't just excluded from the list. E0 is also a member of the set of all possible sequences of 0 and 1. Therefore, the exclusion of E0 from the list proves that the set of all possible sequences of 0 and 1 cannot be listed. But earlier in this thread, I showed that the set of all finite sequences can be listed. I then applied the diagonal argument to this list to obtain an E0 that is excluded from the list. However, in this case the E0 obtained was also not a finite sequence, and therefore a proof using the diagonal argument that the set of all finite sequences cannot be listed fails. This is just plain silly and brings to mind the term "cargo cult mathematics". One point that you've overlooked is that one doesn't need to consider sequences to prove Cantor's theorem. One can prove Cantor's theorem using sets, and the mappings between their elements and their subsets. So, if you're focusing specifically on sequences, then that won't invalidate proofs based on alternative notions. But one can still make statements that are true for every element of an infinite set. I never suggested that Cantor was infallible. And everyone makes mistakes every now and then. So what? If there was an error in Cantor's proof, then the error isn't just Cantor's, it's all the people who have accepted Cantor's proof as valid, including myself. So, you have to do better than mention Cantor's fallibility. What about the fallibility of everyone else who accepted Cantor's proof? Of course it's irrelevant. We're talking about a mathematical theorem, not Mein Kampf. The validity of a mathematical theorem is self-evident, not based on the author. -
[math]\times\!\!\!\!\phi^2[/math]
-

problem with cantor diagonal argument
KJW replied to phyti's topic in Linear Algebra and Group Theory
[Here you agree E0 is a member of L, which represents M.] [Here you say E0 is not a member of L, which represents M. ?] You think I contradicted myself, don't you? That's because you fail to distinguish between the set of sequences and the list of sequences. You fail to recognise that there are sequences in the set of sequences that are not in the list of sequences. By failing to recognise this, you are unable to understand Cantor's proof because this is precisely what Cantor is proving. By assuming that the list of sequences has all the sequences that are in the set of sequences and using this assumption in an attempt to disprove Cantor's theorem, you are begging the question. By "the list is incomplete", I mean that there are sequences in the set that are not in the list, and that is precisely what Cantor is proving. Having "no last member" doesn't come into it. But by assuming that there is only one infinite, you are assuming that Cantor's theorem is false in your attempt to disprove Cantor's theorem, again begging the question. -

problem with cantor diagonal argument
KJW replied to phyti's topic in Linear Algebra and Group Theory
In terms of what this thread is about... no. But if you invoke physical reality, I will call foul. In your paper, you said that L is a binary tree graph that represents the Cantor set M. Then yes, E0 must be a member of L. That is actually a part of Cantor's proof. But it is not what the diagonal argument is about. It seems to me that you don't really understand what it is that Cantor is proving. The sequence formed by negation of the diagonal is an element of the set of all the possible sequences (it is represented in the binary tree graph). This is actually important to Cantor's proof and is why the negation of the diagonal is made of the same symbols as the sequences. When the sequences are placed into a list, the diagonal argument shows that although the negation of the diagonal belongs to the set of sequences, it does not belong to the list of sequences. Thus, the list of sequences is incomplete, proving that the set of sequences has a higher transfinite cardinality than the list of sequences, which has a transfinite cardinality of [math]\aleph_0[/math]. You appear to fail to distinguish between the set of sequences and the list of sequences, which is what Cantor's proof is about. -

Proportion of the area covered by circles
KJW replied to Dhamnekar Win,odd's topic in Applied Mathematics
Not stated but used in the solution is the series expansion of [math]\cos \phi[/math]: [math]\cos \phi = 1 - \dfrac{\phi^2}{2} + \dfrac{\phi^4}{24} - \dfrac{\phi^6}{720} + \cdots = \displaystyle \sum_{j=0}^{\infty} \dfrac{(-1)^j}{(2j)!} x^{2j}[/math] For [math]\phi \approx 0[/math], the terms after [math]\dfrac{\phi^2}{2}[/math] can be ignored, and the closer [math]\phi[/math] is to [math]0[/math], the better [math]1 - \dfrac{\phi^2}{2}[/math] is as an approximation of [math]\cos \phi[/math]. In the limit of [math]\phi \to 0[/math] ([math]n \to \infty[/math]), the approximation is effectively exact. But [math]\phi[/math] can't be exactly [math]0[/math] ([math]\cos 0 = 1[/math]) because then the ratio of the total area of the small circles to the area of the large circle in the limit of [math]n \to \infty[/math] becomes indeterminate. Thus: [math]\cos^2 \phi = (1 - \dfrac{\phi^2}{2})^2 = 1 - \phi^2 + \dfrac{\phi^4}{4} = 1 - \phi^2[/math] for [math]\phi \to 0[/math] (ignoring the [math]\dfrac{\phi^4}{4}[/math] term) [math]2(1 + \cos \phi) = 2 + 2(1 - \dfrac{\phi^2}{2}) = 4 - \phi^2[/math] for [math]\phi \to 0[/math] Also, solving the quadratic equation involved carefully ignoring the higher order terms, leaving only the term that is linear in [math]\phi[/math]. -

Proportion of the area covered by circles
KJW replied to Dhamnekar Win,odd's topic in Applied Mathematics
I don't know where you got those numbers from, but have you interpreted [math]\alpha (R-r)[/math] as [math]\alpha[/math] as a function of [math]R-r[/math] instead of [math]\alpha[/math] multiplied by [math]R-r[/math]? [math]\alpha[/math] is the ratio of the radius of the second outermost circle to the radius of the outermost circle. It is also the ratio of the distance between the centre of the large circle and the center of the second outermost circle to the distance between the centre of the large circle and the center of the outermost circle. Thus, [math]\alpha r[/math] is the radius of the second outermost circles, and [math]\alpha (R-r)[/math] is the distance between the centre of the large circle and the center of the second outermost circle. I chose to define the ratio [math]\alpha[/math] rather than the radius and distance themselves. Much of the solution was about finding the value of [math]\alpha[/math], and even then, only for very large values of [math]n[/math]. It should be noted that the same value [math]\alpha[/math] describes both ratios because the second and subsequent outermost layers of circles are scaled down versions of the outermost layer of circles. -

Entanglement can be demonstrated by measuring the spin of a photon
KJW replied to Paulsrocket's topic in Speculations
I know it's off-topic, but I feel the need to say that the message of the article is for people to keep up-to-date with their COVID-19 booster shots, not that the COVID-19 vaccines do not work! -
The outer event horizon would expand in accordance with the extra mass of the infalling black hole, but the inner event horizon would remain intact as the boundary from which light can't even escape to inside the outer black hole.
-
The Proof of the 3X + 1 Conjecture
-
I have read the suggestion that the universe, represented by the Friedmann-Lemaître-Robertson-Walker (FLRW) metric, can be regarded as the time-reversal of a collapsing matter black hole. I don't know if this is true, but I do see it as plausible. It should be noted that the radial coordinate of a Schwarzschild black hole is timelike to an observer who is inside. Thus, to an observer inside the black hole, the singularity is not located anywhere in space, but in the future. Also, the FLRW metric is conformally flat, which is exactly not the spacetime of a Schwarzschild black hole. But the interior of an infalling matter black hole is not a Schwarzschild metric and may be more like the FLRW metric. A black hole can exist inside a larger black hole. Given that nothing special happens when an object crosses the event horizon of a large black hole, it is reasonable to conclude that a small black hole can cross the event horizon of a much larger black hole completely intact.
-
Considering the Schwarzschild metric, there is no upper limit to mass, and therefore no limit to the size and how close to zero the density can be. However, there may be limits at the cosmological scale. For example, I doubt that a black hole can be less dense than the universe as a whole. If the region surrounding a black hole is denser than the black hole, then the total mass of the black hole and the surrounding region would be large enough for the surrounding region to be also inside the black hole.
-

Proportion of the area covered by circles
KJW replied to Dhamnekar Win,odd's topic in Applied Mathematics
-
It's worth pointing out that although for a small black hole, the tidal forces may be so intense as to cause "spaghettification" well outside the event horizon, for an extremely large black hole, the tidal forces may be so weak that one might not even be aware that one has crossed the event horizon. Also, black holes have a peculiar property compared to ordinary matter: the mass of a black hole increases linearly with respect to radius, in contrast to the cube-power for ordinary matter. Thus, extremely large black holes have very low density. One only needs to accumulate enough matter into the large volume to form the large black hole... one doesn't need to compress anything.
-

problem with cantor diagonal argument
KJW replied to phyti's topic in Linear Algebra and Group Theory
No. This is what Wikipedia says about the use of "arbitrary" in mathematics: This is different to "random", which is associated with chance events and probability, neither of which apply to "arbitrary". Are you talking about finite lists of finite sequences, or are you talking about what Cantor is talking about... infinite lists of infinite sequences? It seems to me that you are talking about finite lists of finite sequences, in which case, you can't argue against Cantor, who is talking about infinite lists of infinite sequences. If you are talking about infinite lists of infinite sequences, then you are not taking into account the infinite nature of the sequences and lists. -

Proportion of the area covered by circles
KJW replied to Dhamnekar Win,odd's topic in Applied Mathematics
With the solution to the second problem in place, I decided to provide a solution to the generalised intermediate version of this problem, where the first and second problems are the two extremes. Because much of the solution to the second problem is unchanged in the solution to the generalised problem, I shall only include the parts of the solution that have changed. Let [math]\sigma[/math] be a parameter, [math]0 \leqslant \sigma \leqslant 1[/math], such that [math]\dfrac{\sigma \pi}{n}[/math] is the angle between the line joining the centre of the large circle to the centre of the outermost circle and the line joining the centre of the large circle to the centre of the nearest second outermost circles. Applying the law of cosines and continuing as shown in solution to the second problem: [math](1 + \alpha)^2 \cos^2\dfrac{\pi}{n} - 2 (1 + \alpha) (1 + \cos\dfrac{\sigma\pi}{n}) + 2 (1 + \cos\dfrac{\sigma\pi}{n}) = 0[/math] Note that the angle associated with [math]\cos^2\dfrac{\pi}{n}[/math] has a different origin to the angle associated with [math]1 + \cos\dfrac{\sigma\pi}{n}[/math]. [math]\phi = \dfrac{\pi}{n}[/math] [math](1 + \alpha)^2 \cos^2\phi - 2 (1 + \alpha) (1 + \cos\sigma\phi) + 2 (1 + \cos\sigma\phi) = 0[/math] [math]\phi \approx 0[/math] , [math]\cos\phi \approx 1 - \dfrac{1}{2} \phi^2[/math] : [math](1 + \alpha)^2 (1 - \phi^2) - (1 + \alpha) (4 - \sigma^2 \phi^2) + (4 - \sigma^2 \phi^2) = 0[/math] Solving the quadratic equation for [math](1 + \alpha)[/math] : [math]1 + \alpha = \dfrac{(4 - \sigma^2 \phi^2) - \sqrt{(4 - \sigma^2 \phi^2)^2 - 4 (1 - \phi^2)(4 - \sigma^2 \phi^2)}}{2 (1 - \phi^2)}[/math] [math]1 + \alpha = \dfrac{(4 - \sigma^2 \phi^2) - \sqrt{(16 - 8 \sigma^2 \phi^2 + \sigma^4 \phi^4) - (16 - (16 + 4 \sigma^2) \phi^2 + 4 \sigma^2 \phi^4)}}{2 (1 - \phi^2)}[/math] [math]1 + \alpha = \dfrac{(4 - \sigma^2 \phi^2) - \sqrt{(16 - 4 \sigma^2) \phi^2 - (4 \sigma^2 - \sigma^4) \phi^4}}{2 (1 - \phi^2)}[/math] [math]1 + \alpha = 2 - \sqrt{4 - \sigma^2}\>\phi[/math] [math]\alpha = 1 - \sqrt{4 - \sigma^2}\>\dfrac{\pi}{n}[/math] [math]1 - \alpha^2 = 2 \sqrt{4 - \sigma^2}\>\dfrac{\pi}{n}[/math] [math]\displaystyle \lim_{n\to\infty} P = \dfrac{\pi}{2 \sqrt{4 - \sigma^2}}[/math] For problem #1, [math]\sigma = 0:[/math] [math]\displaystyle \lim_{n\to\infty} P = \dfrac{\pi}{4}[/math] For problem #2, [math]\sigma = 1:[/math] [math]\displaystyle \lim_{n\to\infty} P = \dfrac{\pi}{2 \sqrt{3}}[/math] -

Proportion of the area covered by circles
KJW replied to Dhamnekar Win,odd's topic in Applied Mathematics
The following is a solution to the second problem: Let [math]R[/math] be the radius of the large circle. Let [math]r[/math] be the radius of the small circles in the outermost layer. Let [math]\alpha r[/math] be the radius of the small circles in the second outermost layer. Let [math]n[/math] be the number of small circles around the circumference of the large circle. Let [math]P[/math] be the proportion of the area of the large circle covered by small circles for [math]n[/math] small circles around the circumference of the large circle. Partitioning the large circle into [math]n[/math] sectors, the area of each sector is: [math]= \dfrac{\pi R^2}{n}[/math] The total area of small circles covering a sector: [math]= \pi r^2 (1 + \alpha^2 + \alpha^4 + \alpha^6 + \cdots) = \dfrac{\pi r^2}{1 - \alpha^2}[/math] Then the proportion of the area of a sector covered by small circles: [math]P = \dfrac{n r^2}{(1 - \alpha^2) R^2}[/math] [math]\dfrac{r}{R - r} = \sin\dfrac{\pi}{n}[/math] [math]r = (R - r) \sin\dfrac{\pi}{n}[/math] [math]r (1 + \sin\dfrac{\pi}{n}) = R \sin\dfrac{\pi}{n}[/math] [math]\dfrac{r}{R} = \dfrac{\sin\dfrac{\pi}{n}}{1 + \sin\dfrac{\pi}{n}}[/math] [math]P = \dfrac{n\>\sin^2\dfrac{\pi}{n}}{(1 - \alpha^2) (1 + \sin\dfrac{\pi}{n})^2}[/math] Let [math](1 - \alpha^2) = \beta \dfrac{\pi}{n}[/math] [math]\displaystyle \lim_{n\to\infty} P = \dfrac{n\>\left( \dfrac{\pi}{n} \right)^2}{\beta\>\dfrac{\pi}{n}} = \dfrac{\pi}{\beta}[/math] Applying the law of cosines: Note that [math](1 + \alpha) r[/math] is the distance between the centres of the outermost and nearest second outermost circles, and that [math](R - r)[/math] and [math]\alpha (R - r)[/math] are the distances from the centre of the large circle to the centres of the outermost circle and second outermost circle, respectively. [math](1 + \alpha)^2 r^2 = (1 + \alpha^2) (R - r)^2 - 2 \alpha (R - r)^2 \cos\dfrac{\pi}{n}[/math] [math](1 + \alpha)^2 \dfrac{r^2}{(R - r)^2} = 1 + \alpha^2 - 2 \alpha \cos\dfrac{\pi}{n}[/math] [math]\dfrac{r}{R - r} = \sin\dfrac{\pi}{n}[/math] [math](1 + \alpha)^2 \sin^2\dfrac{\pi}{n} = 1 + \alpha^2 - 2 \alpha \cos\dfrac{\pi}{n}[/math] [math](1 + \alpha)^2 \sin^2\dfrac{\pi}{n} = (1 + \alpha)^2 - 2 \alpha (1 + \cos\dfrac{\pi}{n})[/math] [math](1 + \alpha)^2 \cos^2\dfrac{\pi}{n} - 2 \alpha (1 + \cos\dfrac{\pi}{n}) = 0[/math] [math](1 + \alpha)^2 \cos^2\dfrac{\pi}{n} - 2 (1 + \alpha) (1 + \cos\dfrac{\pi}{n}) + 2 (1 + \cos\dfrac{\pi}{n}) = 0[/math] Let [math]\phi = \dfrac{\pi}{n}[/math] [math](1 + \alpha)^2 \cos^2\phi - 2 (1 + \alpha) (1 + \cos\phi) + 2 (1 + \cos\phi) = 0[/math] Also let [math]\phi \approx 0[/math] [math]\cos\phi \approx 1 - \dfrac{1}{2} \phi^2[/math] [math](1 + \alpha)^2 (1 - \phi^2) - (1 + \alpha) (4 - \phi^2) + (4 - \phi^2) = 0[/math] This is a quadratic equation to be solved for [math](1 + \alpha)[/math]. However, only the lesser of the two solutions is of interest. [math]1 + \alpha = \dfrac{(4 - \phi^2) - \sqrt{(4 - \phi^2)^2 - 4 (1 - \phi^2)(4 - \phi^2)}}{2 (1 - \phi^2)}[/math] [math]1 + \alpha = \dfrac{(4 - \phi^2) - \sqrt{(16 - 8 \phi^2 + \phi^4) - (16 - 20 \phi^2 + 4 \phi^4)}}{2 (1 - \phi^2)}[/math] [math]1 + \alpha = \dfrac{(4 - \phi^2) - \sqrt{12 \phi^2 - 3 \phi^4}}{2 (1 - \phi^2)}[/math] [math]1 + \alpha = 2 - \sqrt{3} \phi[/math] [math]\alpha = 1 - \sqrt{3} \phi[/math] [math]\alpha^2 = 1 - 2 \sqrt{3} \phi + 3 \phi^2[/math] [math]1 - \alpha^2 = \beta \dfrac{\pi}{n} = 2 \sqrt{3} \phi = 2 \sqrt{3} \dfrac{\pi}{n}[/math] [math]\beta = 2 \sqrt{3}[/math] Therefore: [math]\displaystyle \lim_{n\to\infty} P = \dfrac{\pi}{2 \sqrt{3}}[/math] -

problem with cantor diagonal argument
KJW replied to phyti's topic in Linear Algebra and Group Theory
The flaw is his definition of a diagonal sequence/string/s. It depends on all s listed, and differs from those. He defines the initial list as consisting of horizontal s. That's why the random properties of the s and the list which is itself a random s are included. If the s are parallel there can't be any influence of one on any other. I.e. they are independent. Where did you get the idea that the sequences are random? The more correct term is "arbitrary", which is not the same as "random". In fact, Cantor attempts to construct an infinite list of all possible infinite sequences. But regardless of how that is attempted (represented by a list of arbitrary sequences), the list will always be missing the sequence constructed from the negation of the diagonal. In the case of finite sequences, which Cantor does not consider, one can form a complete list of all possible sequences. But then the diagonal argument becomes establishing that the list of sequences is longer than the sequences themselves. It seems to me that you are placing too much importance on the structure of the list of sequences while not placing enough importance on what the diagonal argument is saying. False. I use the infinite set N. False. Where do you use the infinite set [math]\mathbb {N}[/math]? In an earlier post you said: "Per the constructivist view, no one can nor have formed an infinite list. No one can even form an infinite sequence!" If that's not denying the existence of infinite lists and infinite sequences, then what is? I see nothing wrong with the notion of going from the finite to the infinite. It's a qualitative transition that does not imply a "magic [math]n[/math]". Those are the only ones we can form. No one has or can produce an infinite list. It's not an abstraction but a fantasy. No one will ever see a list for the set N. I realised after had I posted that what I said was ambiguous. And you chose the unintended interpretation. I didn't mean that it was incorrect to apply Cantor's diagonal argument to finite lists of finite sequences. I meant that your application of Cantor's diagonal argument was incorrect. Specifically, you drew the wrong conclusion from the length of the list being longer than the length of the sequences. Also, because Cantor was dealing with infinite lists of infinite sequences, your dealing with finite lists of finite sequences is largely irrelevant. I should remark that although Cantor's diagonal argument applied to infinite lists of infinite sequences only produces one missing sequence (the negation of the diagonal), in fact the cardinality of missing sequences is the same as the cardinality of all possible sequences. Any list of sequences is a proverbial drop in the ocean compared to the set of all possible sequences. -

Why is it so hard to explain time? (What is time?)
KJW replied to chron44's topic in Classical Physics
I should point out that I am considering what time is to be distinct from what time does, although it is understandable if people conflate these two notions. -

problem with cantor diagonal argument
KJW replied to phyti's topic in Linear Algebra and Group Theory
But you have not shown that Cantor's diagonal argument is false. All you have done is denied the existence of infinite lists and infinite sequences. And you are incorrectly applying Cantor's diagonal argument to finite lists of finite sequences. -

Why is it so hard to explain time? (What is time?)
KJW replied to chron44's topic in Classical Physics
Another important consideration is that there are three space dimensions and one time dimension. If instead there were two space dimensions and two time dimensions, as indicated by the signs of the metric coefficients, then although space and time would still be distinct, they would be indistinguishable because the sign of a metric coefficient does not itself indicate whether the component is a space or time component. This would manifest itself in the solution of the wave equation. If my quest not was meaningful - it would be metaphysics. If my quest is meaningful - it is physics. Because physics is meaningful. In that case, time is what is measured by clocks. Can any other statement of what time is be truly meaningful? -

problem with cantor diagonal argument
KJW replied to phyti's topic in Linear Algebra and Group Theory
Thank you. The flaw in your argument is that Cantor was dealing with infinite lists of infinite sequences, whereas you chose to reject the notion of infinite lists of infinite sequences and instead deal with finite lists of finite sequences, and in doing so, misapplied the diagonal argument. In fact, your argument against the diagonal argument actually proved Cantor's theorem in the case of finite lists of finite sequences. In the case of finite sequences, one can always create a finite list of all of them. Therefore, if one applies the diagonal argument to a finite list of all the possible finite sequences, then naturally the negation of any diagonal will form a sequence that is part of the list not covered by the diagonal. That the total number of sequences is greater than the length of the sequences is actually what Cantor's theorem is saying in the case of finite sequences. But when one considers infinite sequences, the total number of possible sequences cannot be listed, as proven by the diagonal argument.