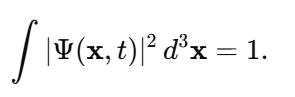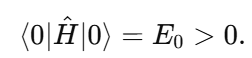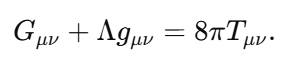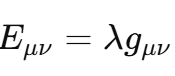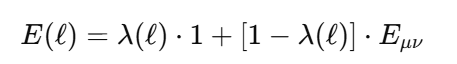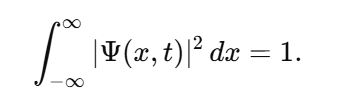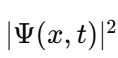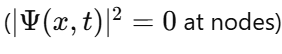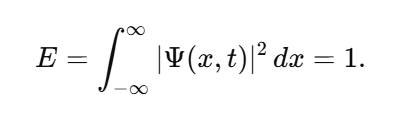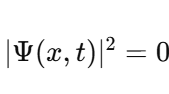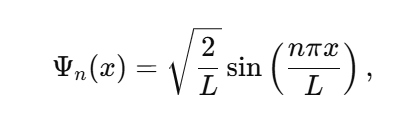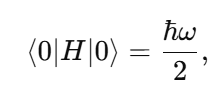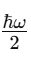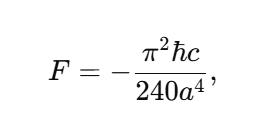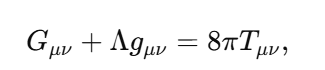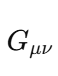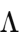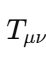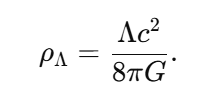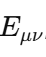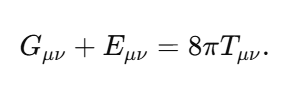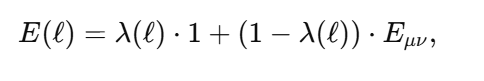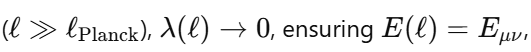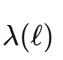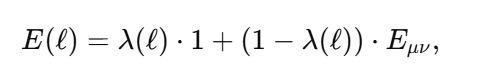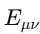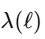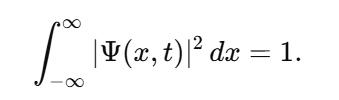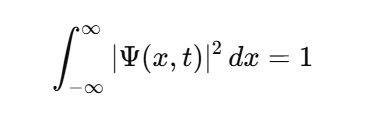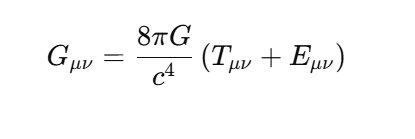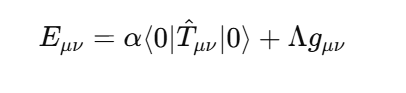ovidiu t
Senior Members-
Posts
30 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Everything posted by ovidiu t
-
Published originally on Zalando : DOI : 10.5281/zenodo.14618602
-
Existence Theory: A Foundational Framework for Understanding Universal Dynamics Summary: The Existence Theory introduces a groundbreaking framework for comprehending the intrinsic quality of existence across all scales, from the quantum realm to the vastness of cosmic structures. At its core, the theory posits that existence inherently resists absolute voids, ensuring the persistence of "something" throughout the universe. Combining philosophical inquiry with robust mathematical modeling, the work formulates a universal equation that unifies density, entropy, and spacetime curvature into a dynamic interplay. Validated through simulations across quantum phenomena, black holes, the Big Bang, and cosmic voids, the theory redefines singularities not as infinite densities but as extremal states of existence. It offers a bold perspective on the universe as a cyclic entity, oscillating between phases of emergence and dissolution, governed by the balance between something and nothing. The Existence Theory not only deepens our understanding of quantum gravity and cosmology but also challenges prevailing notions about the origins and structure of the universe. Its implications pave the way for future explorations into the interconnectedness of physics, philosophy, and emergent phenomena, providing a unified vision of reality. Existance_Theory (4).pdf
-
do you want to read it ?
- 8 replies
-
-1
-
I don't know. maybe. maybe not. if you want we take a look together at the paper...?
-
I would like to share a discovery that feels like a genuine breakthrough. It has been present all along, right under our feet and in front of our eyes, in its beautiful simplicity and astonishing precision. I find myself deeply moved and momentarily at a loss for words, as I believe I have gained an understanding that is fundamentally transformative. Please note that this post was intended to serve as a comment on “The Existence Boundary: A Foundational Principle in Cosmology and Quantum Physics?” Unfortunately, that thread was closed, making it impossible to add my remarks there. I plan to share more details as soon as I am able. The title of this work is: A Theory of Unification: The Persistence Principle. The answer was the hypergraphs!
- 8 replies
-
-1
-
1. Core Idea: Absolute Nothingness vs. Localized Nothingness My proposal emphasizes a fundamental principle: absolute nothingness is impossible. While localized nothingness (e.g., a node in a wavefunction or an isolated vacuum region) can exist, the entire framework—the universe or physical reality—always contains something. This idea is rooted in well-established physics: Quantum Mechanics: Wavefunction normalization ensures total probability is always 1, even if parts of the system have zero probability:(overleaf issues while transporting it here, until I figure it out I will put capture screens, I appologize) Quantum Field Theory: Vacuum fluctuations mean even “empty” space is never truly empty: General Relativity: Baseline spacetime curvature (e.g., from a cosmological constant) ensures the universe retains structure even in the absence of matter: These principles converge into a single boundary condition: nothingness is possible only in localized regions, but never globally across the entire framework. 2. Response to Adds Nothing New If EμνE_{\mu\nu}Eμν were merely a constant multiple of the metric (λgμν\lambda g_{\mu\nu}λgμν) at all scales, it would indeed replicate the behavior of a cosmological constant (Λgμν\Lambda g_{\mu\nu}Λgμν) and add no new physics. However, my proposal introduces a scale-dependent transformation of E: At quantum scales, E acts as a scalar condition enforcing global normalization (or conservation of existence). At macroscopic scales, EμνE_{\mu\nu}Eμν emerges as a tensorial contribution to spacetime curvature. This is conceptually similar to a phase transition, where the same principle (e.g., H₂O) manifests in different forms (liquid vs. vapor) depending on external conditions. The novelty lies in this transition across scales. 3. Addressing the Valid Tensor Criticism (with Thermodynamic Analogy) I acknowledge the concern that an equation like: is not tensorially valid as written. It was meant as a conceptual shorthand for how EEE shifts from a scalar role to a tensorial one depending on the scale ℓ\ellℓ. To clarify this transition, I propose the thermodynamic analogy: In thermodynamics, a substance like water undergoes phase transitions depending on external conditions, such as temperature and pressure. For instance: Below 100∘100^\circ100∘C (at standard pressure), water exists in the liquid phase, with distinct properties like incompressibility. Above 100∘100^\circ100∘C, it transforms into a gas phase, with entirely different properties like diffusivity. Despite these differences, the underlying substance (H₂O) remains the same—it simply exhibits different behaviors in different regimes. Similarly, in my framework: Below the Planck scale (ℓ≪ℓPlanck\ell \ll \ell_\text{Planck}ℓ≪ℓPlanck), EEE behaves as a scalar condition (e.g., E=1E = 1E=1), ensuring global wavefunction normalization and prohibiting absolute void at the quantum level. Above the Planck scale (ℓ≫ℓPlanck\ell \gg \ell_\text{Planck}ℓ≫ℓPlanck), EμνE_{\mu\nu}Eμν emerges as a tensorial contribution to spacetime curvature, ensuring a baseline structure even in macroscopic “vacuum” regions. The Planck scale acts as a tipping point, analogous to the boiling point of water, where the underlying principle of existence (like the substance H₂O) remains constant but manifests differently depending on the regime. Rigorous Mathematical Path Forward: The transition can be formalized using a scale-dependent parameter λ(ℓ)\lambda(\ell)λ(ℓ), which smoothly interpolates between the two regimes: 4. Experimental Constraints on Vacuum Solutions I recognize the strength of observational data supporting standard GR with a small or negligible Λ\LambdaΛ in local vacuum solutions. My framework is consistent with these constraints because: At everyday and astrophysical scales, the effects of EEE (or λ(ℓ)\lambda(\ell)λ(ℓ)) are negligible, ensuring no observable deviations from standard GR. Only under extreme conditions—such as near singularities or at the Planck scale—does EEE deviate significantly from classical GR, potentially preventing singularities or explaining pre-Big-Bang states. 5. Absolute Nothingness in Cosmic Contexts This principle offers a fresh perspective on two major questions: Before the Big Bang: If absolute nothingness is impossible, then the Big Bang could not have emerged from void. Instead, some precursor state must have existed—whether as a quantum phase, a bounce, or another structure within the Existence Boundary framework. End States of the Universe: Even in extreme scenarios like heat death, the Big Crunch, or the Big Rip, the universe cannot vanish entirely. Nonzero vacuum energy, quantum fluctuations, or baseline curvature ensure a persistent “something.” Much like water retains a molecular structure in all phases (solid, liquid, gas), the universe retains a minimal existence across all cosmic scenarios. This ensures continuity of existence even in extreme conditions. 6. Value of the Proposal While the mathematical refinement and rigorous predictions are still in development, the concept offers: Unification: A single boundary condition linking quantum, relativistic, and cosmological domains. Inspiration: A framework for addressing questions like singularity resolution and the nature of pre-Big-Bang existence. Potential for Novel Predictions: For example, detecting signatures of a cosmic bounce in the CMB or deviations in gravitational wave spectra near black holes. Conclusion I recognize the need to refine the mathematical structure of EEE and its tensorial formulation. However, the central principle—that absolute nothingness is impossible, and existence persists across all scales—is a meaningful unification of existing physical insights. By focusing on the transition of EEE between quantum (scalar) and macroscopic (tensorial) regimes, this framework offers a novel lens on some of the universe’s biggest questions: the origins of the Big Bang, the fate of the cosmos, and the resolution of singularities.
-
At any scale—whether quantum, relativistic, or cosmological—absolute nothingness cannot dominate the entirety of the framework in which physical phenomena occur. Even if we imagine the universe condensed into the size of a room, a grain of sand, or stretched infinitely, the probability that the entirety of the framework is filled with "nothingness" is exactly zero. This impossibility arises because: Wavefunction Normalization: In quantum mechanics, the total probability across all of space must sum to 1. Even if local regions (nodes) show zero probability, other regions must compensate with nonzero values. This guarantees that "something" must always exist somewhere within the framework. Quantum Fluctuations: In quantum field theory, the vacuum is not empty but filled with fluctuations that generate virtual particles. This activity means "nothingness" is never truly realized, even in the smallest scales or "empty" regions. Spacetime Curvature: In general relativity, spacetime itself is never devoid of energy or structure. Even "empty" space maintains energy density (e.g., the cosmological constant), ensuring the persistence of something—whether vacuum energy, dark energy, or the geometry of spacetime itself. Scaling the Framework: Whether the framework is as small as a particle or as vast as the cosmos, these principles remain valid. The fundamental laws of physics ensure that some form of existence—energy, fluctuations, or curvature—persists, preventing the framework from being completely devoid of all existence.
-
Localized Nothingness (Nodes): Nodes, where the probability density is zero in the wave function, represent localized nothingness. However, they are always within a broader wave function where the probability density is nonzero elsewhere. In this sense, nodes do not represent total nothingness; instead, they are surrounded by something. They are part of a system where the normalization condition guarantees that the total probability sums to 1. Distinction Between Local and Total Nothingness: My claim does not deny localized regions of zero probability, such as nodes. I am asserting that total nothingness within a system or framework is impossible. Even if one region or point within a system has no particles, energy, or matter, the system as a whole will have "something" elsewhere to ensure the total probability remains normalized. Implication of the Existence Boundary: The Existence Boundary (E) posits that the universe cannot reach a state of total nothingness. While localized regions of "nothingness" may exist (e.g., nodes), they are always embedded within a system where "something" persists globally. If the probability of "nothingness" approaches 99.999...% in one region, normalization ensures that the remaining probability, no matter how small, must manifest as something elsewhere. Why Absolute Nothingness is Impossible: Total nothingness would imply a global absence of all energy, matter, or structure, violating principles like wave function normalization, vacuum fluctuations (quantum field theory), and spacetime curvature (general relativity). Localized nothingness is always "bounded" by the presence of existence elsewhere, ensuring that "something" must always exist in the broader framework. Conclusion: I am not claiming that "nowhere there is nothingness." Instead, I assert that total nothingness across an entire system or framework is impossible. Localized nothingness, such as nodes in a wave function, is entirely consistent with the Existence Boundary, as they exist within a broader framework where something must always be present. This refined claim emphasizes the impossibility of global nothingness while acknowledging the reality of localized phenomena like nodes. It aligns with established principles and ensures clarity in addressing your critique.
-
1. Wavefunction Normalization and Nonzero Total Probability The wavefunction in quantum mechanics must satisfy the normalization condition: Local Probability: represents the probability density at position x. At any single point x, this probability can be zero (e.g., nodes in the wavefunction). Global Constraint: The integral over all space ensures that the particle exists somewhere with total probability : Implication for E: The Existence Boundary extends this principle to the entire universe, ensuring that while there may be local absences the global probability of existence remains conserved: 2. Nodes in Quantum Mechanics In quantum systems, nodes represent regions where , but this does not imply nothingness: Mathematical Example: Consider the wavefunction for a particle in a 1D box: where n is the quantum number, and L is the box length. At specific points: forming nodes. However, the wavefunction is nonzero elsewhere, ensuring global existence. Implication for E: Nodes are consistent with E. Local absence does not negate global existence, which is guaranteed by the wavefunction's normalization. 3. Quantum Field Theory: Vacuum Fluctuations In QFT, even the vacuum has nonzero energy and fluctuations:where H is the Hamiltonian and represents the zero-point energy of the quantum harmonic oscillator. Casimir Effect: The attractive force between uncharged conducting plates arises from differences in vacuum energy: where a is the separation between the plates. Lamb Shift: A shift in energy levels of hydrogen due to vacuum fluctuations provides further evidence of nonzero vacuum properties. Implication for E: Vacuum fluctuations are a direct manifestation of E, showing that the vacuum is not "nothing" but a dynamic state filled with energy and activity. 4. General Relativity: Spacetime Structure The Einstein field equations describe spacetime curvature caused by energy and matter: where is the Einstein tensor, is the cosmological constant, and is the stress-energy tensor. Cosmological Constant Λ\LambdaΛ: Represents vacuum energy density, ensuring spacetime curvature persists even in the absence of matter: Implication for E: The Existence Boundary can be expressed as an additional termenforcing a minimum curvature or energy density: Unified Mathematical Representation of E Emergence refers to the phenomenon where higher-order properties (e.g., macroscopic or relativistic effects) arise naturally from the collective behavior of fundamental interactions or principles at smaller scales (e.g., quantum scales). In the context of the Existence Boundary (E), the emergence describes the transition of E from a scalar form at the quantum level to a tensor form at relativistic or macroscopic scales. Unified Mathematical Representation of E: Explanation The proposed scale-dependent formulation of E captures this emergent behavior mathematically: where: - is a scale-dependent interpolation function that smoothly transitions between quantum and relativistic regimes. - At quantum scales At relativistic/macroscopic scales: a rank-2 tensor. The emergent behavior is captured in the mathematical interpolation, where the properties of E evolve naturally as a function of the scale ℓ\ellℓ. Role of Scale Interpolation Function The function λ(ℓ)\lambda(\ell)λ(ℓ) governs the scale-dependent behavior of E. It can be explicitly defined as: where:This function ensures a smooth, continuous transition between quantum and relativistic scales, avoiding abrupt discontinuities. Emergent Transition from Scalar to Tensor: Relation to the Emergence Phenomenon The mathematical interpolation and scale-dependent transition of E reflect a key feature of emergence: At small scales, the Existence Boundary (E) enforces probabilistic constraints, ensuring that something must exist (quantum normalization). As scale increases, the cumulative effects of these constraints manifest as geometric properties, contributing to the curvature and structure of spacetime This emergence mirrors how: Quantum fluctuations give rise to macroscopic phenomena like vacuum energy. The statistical behavior of individual particles transitions into thermodynamic laws at larger scales Observable Implications Quantum Regime: Virtual particles and vacuum fluctuations (Casimir effect, Lamb shift) manifest as direct consequences of E at small scales. Macroscopic Regime: contributes to preventing singularities, supporting scenarios like the Big Bounce in cosmology. Intermediate Scales: The smooth transition governed by may influence phenomena like Hawking radiation near black holes or the early universe's inflationary phase. Conclusion: A Unified Perspective on the Existence Boundary (E) The Existence Boundary (E) offers a unifying framework that ties together fundamental principles from quantum mechanics, quantum field theory, and general relativity to address the impossibility of absolute nothingness. Here’s how: Wavefunction Normalization and Global Existence: The Existence Boundary formalizes the principle that while local absence (e.g., nodes in quantum mechanics) is possible, global existence is conserved. This is mathematically guaranteed through wavefunction normalization, extending the principle from single particles to the universe as a whole. Nodes and Vacuum Fluctuations: Nodes in quantum systems and vacuum fluctuations in quantum field theory demonstrate that even in regions of local absence or "emptiness," the broader system retains dynamic, nonzero properties. E provides a conceptual and mathematical boundary that ensures these fluctuations and dynamic properties are consistent with the impossibility of absolute void. Emergence Across Scales: E evolves naturally from a scalar at quantum scales (enforcing probabilistic constraints) to a tensor at macroscopic scales (manifesting as spacetime curvature). This reflects the phenomenon of emergence, where small-scale principles give rise to large-scale behaviors. The smooth interpolation function ensures a seamless transition, avoiding discontinuities and ensuring the continuity of physical laws across scales. Observable Implications: Quantum Regime: E is consistent with observable phenomena like virtual particles, the Casimir effect, and the Lamb shift. Relativistic Regime: At larger scales, E contributes to the structure and curvature of spacetime, influencing phenomena like the prevention of singularities in black holes and the Big Bounce in cosmology. Intermediate Scales: E offers potential explanations for transitions observed in phenomena like Hawking radiation and early universe inflation. A Foundational Principle: E is not an arbitrary imposition but emerges from established principles, providing a boundary condition that ensures the persistence of existence across all scales. It offers a new perspective on the unification of quantum mechanics and general relativity, addressing fundamental questions about the nature of existence and the structure of reality. Broader Significance: The Existence Boundary reaffirms the interconnectedness of quantum and relativistic phenomena. By emphasizing the impossibility of absolute nothingness, it provides a foundation for understanding the universe's continuity and resilience, even under extreme conditions like black holes or the early moments of the Big Bang. While speculative, E offers a mathematically grounded and physically plausible framework that could inspire further research and exploration. Its observable consequences and alignment with established physics make it a valuable concept in bridging the gaps between different domains of physics.
-
Thank you for your thoughtful engagement! I appreciate the opportunity to clarify and expand on the Existence Boundary (E) concept and address the points raised. Why "Boundary" and Not Just a Principle? The term "boundary" is intentionally chosen to signify a universal constraint rather than a spatial or temporal edge. The Existence Boundary doesn’t denote a physical edge to the universe but instead acts as a limit condition that makes absolute nothingness fundamentally impossible. It is a boundary in the conceptual and mathematical sense, preventing "nothing" from being realized, whether in the quantum vacuum, the fabric of spacetime, or the energy density of the cosmos. This boundary is a necessary condition for existence to manifest across scales, ensuring that the universe cannot reach a state devoid of structure, energy, or potential. Unlike a "principle," which suggests a philosophical or heuristic rule, "boundary" underscores the foundational and universal nature of the idea. Is It Just Restating "Nature Abhors a Vacuum"? While it resonates with the philosophical idea that "nature abhors a vacuum," the Existence Boundary goes much further: It formalizes this concept mathematically, tying it to quantum mechanics (wavefunction normalization), general relativity (vacuum energy and spacetime curvature), and quantum field theory (vacuum fluctuations and virtual particles). It integrates existing physical laws into a unified framework, demonstrating that the impossibility of nothingness is already implicitly enforced across these theories but has not been explicitly articulated as a single foundational boundary. In short, the Existence Boundary aims to unify disparate observations and principles, transforming a philosophical intuition into a precise scientific proposal. Observational and Testable Consequences The idea of the Existence Boundary is not merely philosophical—it has potential observable implications: Quantum Fluctuations and Virtual Particles: Quantum field theory ensures that even the vacuum is "something," filled with fleeting virtual particles. These are observable indirectly through effects like the Casimir effect and the Lamb shift, which align with E’s assertion of the impossibility of a true vacuum. Big Bang and Black Hole Singularities: E proposes that true singularities (e.g., infinite density in black holes or the Big Bang) are mathematically impossible. Instead, the universe undergoes a "bounce" or transition near extreme densities. Observationally, this could appear as deviations in gravitational wave signals or traces of pre-Big Bang phenomena in the cosmic microwave background (CMB). Hawking Radiation: Near black hole horizons, virtual particles arise due to quantum fluctuations. E ensures that these particles and the resulting radiation exist, highlighting that "nothingness" is prevented even under extreme gravitational collapse. Dark Energy and Universe Expansion: E can be linked to the persistence of dark energy, which prevents the universe from collapsing into nothingness and drives its accelerating expansion. Observations of this acceleration provide indirect support for the boundary condition. Wavefunction Collapse: In quantum mechanics, the wavefunction is never zero across all space and time. E ensures that the normalization of the wavefunction (Σ|Ψ|² = 1) is upheld universally, guaranteeing the persistence of existence. Why Is It Scientific? The Existence Boundary does not override existing theories—it extends them: In Quantum Mechanics: It aligns with wavefunction normalization, showing that the probability of existence is always non-zero. In General Relativity: It prevents singularities, aligning with the idea that spacetime must have some minimum structure or curvature. In Quantum Field Theory: It explains the necessity of vacuum fluctuations and virtual particles, reinforcing the impossibility of a true vacuum. While direct testing is challenging, these connections to existing physics suggest ways to indirectly validate the principle through observed phenomena. The Existence Boundary provides a fresh lens to interpret known effects while offering potential predictions for phenomena not yet fully understood. Final Thoughts The Existence Boundary is not about redefining existing laws but rather highlighting a unifying constraint that connects them. It provides a deeper understanding of why "something" must always exist, bridging philosophical intuitions and scientific observations. As such, it stands as both a conceptual and a potentially testable addition to our understanding of the universe. The claim that absolute nothingness is possible contradicts well-established principles in quantum mechanics, quantum field theory, and general relativity. Here's why: 1. Quantum Vacuum Fluctuations The quantum vacuum is not empty but filled with fluctuating fields giving rise to virtual particles. These fluctuations are observable through phenomena like the Casimir effect and Lamb shift, which directly demonstrate that the vacuum has quantifiable, nonzero properties. This provides a strong case against the possibility of absolute nothingness, even in regions considered "empty." 2. Wavefunction Normalization In quantum mechanics, the wavefunction Ψ(x,t) must satisfy the normalization condition: This ensures that the total probability of finding a particle across all space is always 1. While the probability of presence in one specific region can be zero, there is always a nonzero probability elsewhere. This condition rules out absolute nothingness, as it guarantees the existence of something at all times. 3. General Relativity and Spacetime Curvature In general relativity, spacetime itself is a physical entity shaped by the presence of energy and matter. Even in the absence of visible matter, spacetime cannot collapse into absolute nothingness due to the persistence of vacuum energy or dark energy. The cosmological constant Λ\LambdaΛ, for instance, represents a nonzero energy density intrinsic to spacetime. This ensures: The impossibility of a true void in the universe. A minimum energy density that prevents spacetime from becoming truly "empty." Additionally, the Existence Boundary (E) can be seen as an extension of general relativity, ensuring that spacetime itself maintains a baseline structure, even in extreme conditions like black hole interiors or the early universe. The Existence Boundary The Existence Boundary unifies these principles to assert that something must always exist across scales: At quantum scales, wavefunction normalization and vacuum fluctuations ensure nonzero probabilities. At macro scales, spacetime curvature and dark energy ensure the persistence of structure. Across theoretical scales, E acts as a boundary condition, preventing the universe from collapsing into a singularity or absolute nothingness. This assertion is supported not only by quantum mechanics but also by cosmological phenomena like the accelerating expansion of the universe.
-
The Existence Boundary (E) is not designed to replace existing physical laws but rather to formalize an implicit principle: the impossibility of absolute nothingness. While physical laws like quantum mechanics and general relativity address "somethingness" in fragmented ways, the Existence Boundary unifies this observation across scales and theories. 1. Why is this principle necessary? While existing physics (e.g., quantum field theory's vacuum fluctuations and general relativity’s singularities) implies that nothingness is avoided, these implications are scattered and domain-specific. The Existence Boundary explicitly frames this observation as a universal principle, applicable to all scenarios—before the Big Bang, within black holes, or in the vacuum. Instead of positing a physical boundary, the Existence Boundary provides a logical boundary to nothingness, showing why "something" must always exist, regardless of the scale or context. 2. Does it "save the universe" or change physics? No, it doesn’t "save" the universe. Rather, it highlights that physical laws inherently prevent true nothingness. By formalizing this, the Existence Boundary acts as a meta-principle that connects disparate phenomena and ensures coherence across scales. For example: In quantum mechanics, it aligns with the normalization of the wave function: if something doesn’t exist in one place, it must exist elsewhere. In general relativity, it reinforces why singularities might lead to phenomena like Hawking radiation rather than absolute collapse. In cosmology, it suggests why the Big Bang likely emerged from a pre-existing state rather than nothing. 3. What is new here? The Existence Boundary is new in its framing and scope: It proposes that absolute nothingness is universally impossible—not just in specific contexts. It bridges quantum mechanics, cosmology, and general relativity, offering a unifying concept that ties together disparate observations and constraints. It gives a mathematical foundation to something previously only implied, such as ensuring the universe never crosses into absolute nothingness. 4. Is it testable? While directly testing E is challenging, its consequences are indirectly testable: Observations of black hole mergers or Hawking radiation could reveal deviations from singularity models, consistent with E. Anomalies in the cosmic microwave background might hint at pre-Big Bang structures. The behavior of vacuum fluctuations and virtual particles could further affirm the impossibility of nothingness. The Existence Boundary doesn’t propose new physical laws but identifies a unifying principle embedded within them. It clarifies the impossibility of nothingness as a foundational constraint that prevents the collapse of reality into nonexistence. Far from redundant, it complements and enriches current physics while opening pathways for deeper inquiry into the origins and fate of the universe. 1. The Observation Across Fields The Existence Boundary is derived from a simple, universal observation: something must always exist. This is not just a philosophical proposition but a logical extension of what is already observed across quantum mechanics, general relativity, and cosmology. The reasoning begins with a foundational observation: The wave function in quantum mechanics shows that if a particle's presence is zero in one region, it must exist elsewhere (wave function normalization ensures this). Thus, absolute absence is impossible. Vacuum fluctuations in quantum field theory demonstrate that even "empty" space is active, producing temporary particle-antiparticle pairs. This again suggests that nothingness cannot persist. General relativity shows that energy-matter equivalence (E=mc²) ensures the conservation of energy, even in extreme conditions like black holes, preventing the universe from collapsing into a state of true "nothingness." 2. Addressing Nodes and Barriers The critique references nodes in an s orbital or infinite potential barriers, asking whether E is necessary. These concepts are entirely compatible with E: Nodes in quantum mechanics refer to points of zero probability density, but they don’t imply absolute nothingness. Instead, they are part of a broader wave function where probabilities remain nonzero elsewhere. E aligns with this reasoning, stating that if something is absent in one place, it must exist elsewhere. Infinite potential barriers in quantum mechanics represent localized regions where particles cannot exist. However, particles still exist on either side of the barrier. This again demonstrates that while existence can be locally restricted, absolute nothingness is forbidden. E is not about removing nodes or barriers; it formalizes the impossibility of a universe-wide void. 3. Chain of Reasoning for E The reasoning for the Existence Boundary follows these steps: Quantum Mechanics: Wave function normalization guarantees that the sum of probabilities equals 1. This implies the existence of the particle somewhere in the universe. Quantum Field Theory: The principle of least energy suggests vacuum fluctuations. These fluctuations prevent any region from being entirely devoid of existence. General Relativity: Energy conservation prevents the collapse of spacetime into true nothingness. Even singularities maintain some form of energy or information (e.g., Hawking radiation). By connecting these observations, E emerges as a universal boundary condition that applies across scales, from the quantum to the cosmological. 4. Not Unicorns, but Logical Connections The Existence Boundary is not an arbitrary principle added to physics. It is not claiming that empty space must contain random phenomena (like "striped unicorns"). Instead, E frames a universal constraint implied by physics: Virtual particles, dark energy, gravitational waves, and Hawking radiation all point to the impossibility of absolute nothingness. The Existence Boundary doesn’t invent new elements but rather highlights a shared principle across theories. 5. Why E is Necessary Existing theories address specific domains but don’t explicitly rule out the possibility of absolute nothingness: Quantum mechanics deals with probabilities but doesn’t assert that "something must always exist." General relativity focuses on spacetime and mass-energy equivalence but doesn’t formalize the impossibility of nothingness. Cosmology describes the universe’s evolution but doesn’t address what preceded the Big Bang. The Existence Boundary formalizes this shared foundation, creating a unifying principle that spans these domains. 6. Testability E’s implications can be indirectly tested: Wave Function: If normalization fails anywhere, it would challenge E. So far, normalization holds universally. Vacuum Fluctuations: The presence of virtual particles in all "empty" space aligns with E. Gravitational Waves: Deviations in black hole mergers could suggest non-singular collapses, consistent with E. Cosmic Microwave Background: Anomalies in the CMB could hint at pre-Big Bang structures or an eternal universe, both aligning with E. E is not an unnecessary addition to physics. It formalizes what existing theories already imply but don’t explicitly state: the impossibility of absolute nothingness. By uniting observations from quantum mechanics, general relativity, and cosmology, the Existence Boundary offers a powerful tool for understanding the universe’s foundational constraints.
-
Is it new? Yes, E is new because it formalizes the idea that something must always exist and prevents the possibility of absolute nothingness. While similar concepts are present in quantum theory (like vacuum fluctuations and virtual particles) and cosmology (such as energy persistence in black holes), E offers a unified framework that ties together quantum, cosmological, and relativistic scales. This new perspective gives a fresh outlook on old ideas, showing how they might be connected. Is it testable? The direct testability of E is still a challenge, but we can look for indirect signs that support it: Virtual Particles: These quantum fluctuations in the vacuum are a good example of something always existing, even in "empty" space. If E holds, we’d expect these fluctuations to be an ongoing phenomenon, reinforcing the idea that nothingness isn't possible. Cosmic Microwave Background (CMB): We might find subtle fluctuations or anomalies in the CMB that suggest the universe didn't start from a true state of nothingness. This would support the concept that something always existed, even in the very early universe. Gravitational Waves: Observing black hole mergers could reveal small differences in the expected gravitational wave signals, suggesting a non-singular collapse, which supports the Existence Boundary. Hawking Radiation: If Hawking radiation can be detected from small or primordial black holes, the spectrum could show deviations from the standard model, which may align with the idea of energy-preserving behaviors in line with E. So while E itself might not be directly observable, we can test its effects through phenomena like virtual particles, the CMB, gravitational waves, and Hawking radiation. If these observations show patterns that align with E, it could provide indirect evidence of this fundamental principle. The Existence Boundary (E) operates in a slightly different way. Instead of placing a boundary on space itself, E asserts that absolute nothingness—a state where no matter, energy, or structure exists—is impossible. So, rather than a physical boundary in space, the Existence Boundary is more of a principle that applies across all scales (quantum, relativistic, cosmological). It's not a boundary in the traditional sense, but a constraint on what can exist. This means that, in any point in the universe, something must always exist. It doesn't necessarily define the location of that existence, but rather the principle that existence can't be entirely absent, no matter where you are in the cosmos. In essence, E prevents "nothing" from ever being truly realized, ensuring that something must always exist, no matter where you look.
-
In modern physics, the question of what constitutes the fabric of reality has been deeply intertwined with the understanding of singularities, the Big Bang, and vacuum energy. However, one fundamental question has remained underexplored: What guarantees the existence of something in the universe, and why is the concept of "nothingness" ultimately unachievable? This texte attempts to propose a new foundational principle, which we call the Existence Boundary (E). The principle posits that something must always exist, and that this concept holds across quantum mechanics, general relativity, and cosmology. The Existence Boundary (E) operates as a constraint on the physical universe, implying that absolute nothingness — a state where no energy, matter, or structure exists — is an impossibility. This is not only a philosophical statement but also a speculative yet mathematically grounded principle with potential implications for cosmology, quantum field theory (QFT), and the nature of space and time. In this work, we propose a formalization of the Existence Boundary and explore its potential impact on both our understanding of black holes, virtual particles, and the Big Bang. Key Concepts of the Existence Boundary The Impossibility of Absolute Nothingness: The Existence Boundary asserts that the universe cannot reach a state of absolute void. Even in regions that appear "empty" — such as the vacuum of space — quantum fluctuations, vacuum energy, or dark energy ensure that something always exists. This principle is analogous to the cosmological constant Λ\LambdaΛ, which represents a form of energy intrinsic to spacetime itself. General Relativity and the Existence Boundary: In General Relativity, spacetime is curved by the presence of matter and energy. The Existence Boundary can be viewed as an extension of this principle, ensuring that even in the absence of visible matter, spacetime cannot collapse into "nothingness." Instead, the universe will always maintain some energy density, manifesting as vacuum energy or dark energy. This prevents spacetime from becoming truly empty or reaching a singularity where physics breaks down. Quantum Field Theory and the Existence Boundary: In Quantum Field Theory, the vacuum is not truly empty but is filled with quantum fluctuations that give rise to virtual particles. These particles can briefly appear and disappear, but they represent a continuous, underlying "something" that maintains the fabric of reality. The Existence Boundary is consistent with this framework, suggesting that even the "empty" vacuum is full of potential energy and activity, preventing a true vacuum (or absence of energy). Wave Function and the Existence Boundary: In Quantum Mechanics, the wavefunction Ψ(x,t)\Psi(x,t)Ψ(x,t) describes the probability distribution of a particle's location and state. It is a fundamental tool in understanding quantum systems, but it is never zero — implying that there is always some nonzero probability of finding a particle at any given point in space-time. The Existence Boundary can be viewed as an extension of the wavefunction concept, ensuring that the total probability of existence across the entire universe sums to 1: This equation guarantees that there is always a nonzero probability of something existing, regardless of whether it is observable in a given moment or region. This directly connects the probabilistic nature of quantum mechanics to the foundational constraint of Existence — ensuring that no region of space-time is completely devoid of something. Furthermore, this formulation suggests that the Existence Boundary ensures the wavefunction never fully collapses into zero — a principle aligned with quantum mechanics, where even the absence of particles doesn't imply absolute nothingness. The continuous presence of vacuum fluctuations and quantum fields means that something always "exists," even if we cannot always observe it directly. Cosmological Implications: The Existence Boundary offers a solution to the problem of singularities in the Big Bang and the interiors of black holes. By ensuring that something always exists, it implies that the universe’s early state was not a singularity (a point of infinite density and curvature) but rather a bounce or a transition into the current observable universe. Similarly, the interiors of black holes may not collapse into a singularity but instead follow a process consistent with the Existence Boundary, preventing the breakdown of physical laws. Mathematical Formulation of the Existence Boundary The Existence Boundary can be expressed in a form consistent with General Relativity and Quantum Field Theory. The simplest approach is to add a term EμνE_{\mu\nu}Eμν to the Einstein Field Equations that represents the vacuum energy and quantum fluctuations inherent in spacetime. This term prevents the collapse of spacetime into a singularity and ensures the continuity of energy and structure. Where: For the Existence Boundary, we propose that could be modeled by a combination of vacuum energy (quantum fluctuations) and dark energy: Where: This equation ensures that spacetime cannot be empty and that some form of energy exists at all times, whether it manifests as vacuum fluctuations, dark energy, or quantum fields. Predictions and Observable Phenomena Virtual Particles: The Existence Boundary predicts that virtual particles will exist in the quantum vacuum, even in the absence of matter. These particles momentarily appear and interact, leaving observable effects such as the Casimir effect. They provide indirect evidence of the Existence Boundary. Hawking Radiation: Near the event horizon of black holes, virtual particles are created due to quantum fluctuations. This process, known as Hawking radiation, could be seen as a manifestation of the Existence Boundary, where energy is still present near the black hole even in what seems like a "nothing" region. This supports the idea that something always exists, even in extreme conditions. Accelerating Expansion: The Existence Boundary offers a natural explanation for the accelerating expansion of the universe. Dark energy, which is believed to be driving the expansion, could be a manifestation of the underlying energy described by the Existence Boundary. The continuous presence of this energy ensures that the universe's expansion never decelerates and that spacetime is never empty. Big Bang and Big Bounce: The Existence Boundary offers a framework for understanding the Big Bang not as a singularity but as a bounce from a quantum state, where spacetime itself prevents collapse into nothingness. This aligns with models such as Loop Quantum Gravity, which propose that the universe has undergone a bounce rather than originating from a singularity. Conclusion The Existence Boundary is a proposed foundational principle that ensures the continuous presence of something in the universe, preventing the possibility of absolute nothingness. It operates across general relativity, quantum field theory, and cosmology, offering new insights into phenomena such as dark energy, vacuum fluctuations, Hawking radiation, and the Big Bang. By ensuring that spacetime cannot collapse into nothingness, the Existence Boundary provides a possible solution to the problem of singularities and the origin of the universe, suggesting that the Big Bang was not a point of infinite density, but rather a transition or bounce driven by quantum effects. Further research and observations may allow us to refine this idea, potentially linking it to observable phenomena like gravitational waves, vacuum fluctuations, and the acceleration of the universe. The Existence Boundary could serve as a fundamental concept in understanding the nature of space, time, and the universe itself.
-
It doesn't, indeed. It was related to the question of contemplating the present and the individual experience of it. Off topic.
-
I love both farting unicorns and leprechauns. I was referring to a period of classic physics period where this idea of absolute value concerning time reigned (thus my subtle reference to Renaissance) ..too subtle ?! As I was saying the experience of time at individual level is highly subjective and to a large extent, yes, we are subjects of processes that operate on timescales so short they feel instantaneous. These processes are essential for navigating the world, allowing us to react to immediate dangers, make quick decisions, and process sensory information at speeds that support fluid interaction with our environment. Having that in mind there is a difference between the perception of instantaneity and the actual temporal dynamics involved. From a neuropsychological standpoint, what is perceived as instantaneous is the result of highly efficient, but not temporally zero, processing times. It was clumsy from my side to write that thought without further explanations, as remarked by another participant.
-
Some of our processes are instantaneous. I am particular thinking at driving experience, for example. And I agree with the idea of building a "virtual present" The experience of time at individual level is highly subjective. Coming back to the question : "Could we observe the present ?". The speculative answer would be yes. if we have a fixed point in the univers, an absolute clock somewhere …(but it sounds so...Renaissance )
-
Must be some species preservation mechanisms. Joggling between "past" experiences and "predicting on the go" the present?
-
a bit off topic: at individual level, the way the consciousness is "awake" and building the reality is already altering the process of understanding the present or it has something to do with it. I am referring at "time slices" of consciousness every 400 millisecondes. The present is the prisoner of the law of synchronicity/simultaneity (two events occurring at the same time are perceived differently depending on the observer's frame of reference). To grasp the present, Time would need to be absolute in value.
-

Inquiry : Spacetime Ruptures and Bidirectional Time
ovidiu t replied to ovidiu t's topic in Speculations
I apologize. It mainly tries to solve AMPS paradox by EPR approach: 1. Entanglement of "space" in vacuum 2. Entangled Black holes (so it implies "un" entangled black holes) 3. Entanglement as a phenomenon generating/ creating spacetime 4. Entanglement quantum phenomenon bridging GR and QFT I suppose the scientist needs no introduction. He's part of the team working/starting string theory. -

Inquiry : Spacetime Ruptures and Bidirectional Time
ovidiu t replied to ovidiu t's topic in Speculations
-

Inquiry : Spacetime Ruptures and Bidirectional Time
ovidiu t replied to ovidiu t's topic in Speculations
This was somewhat expected, an inevitable trajectory for General Relativity (GR) when considering very small scales and gravity. There are no surprises there. From this conversation, I am taking some points: Philosophers must follow compulsory courses in physics, and physicists must follow courses in philosophy! GR is effective on large scales but overlooks the quantum scale, which can lead to a metaphorical 'stiff neck' from trying to reconcile its implications. QFT becomes essential when dealing with massive black holes. At the quantum level, uncertainty reigns supreme, guiding the behavior of nature. Though, in the eyes of a profane, it looks like you can't have a piece of knowledge if you don't trade their piece of knowledge... 'Singularity' might just be a term for our current lack of understanding. No bridge yet (except string theory ? ) between big things and small things. Intuitively, this sheds some light on my initial question: the singularity at r=0 isn't a location; it's a moment in time, or more precisely, many locations along a time-like curve. I'm assuming that space in this scenario could resemble crumpled paper. Yet, I would like to know if this 'crumpled paper' has a breaking point, despite knowing that any analogy is inadequate when facing such counterintuitive levels and forces at play. Thank you all! @Moderators: feel free to close the subject, though unsolved. I have seen my mistakes of conception and methodology. -

Inquiry : Spacetime Ruptures and Bidirectional Time
ovidiu t replied to ovidiu t's topic in Speculations
This was the initial question. And this is the answer I was looking for. -

Inquiry : Spacetime Ruptures and Bidirectional Time
ovidiu t replied to ovidiu t's topic in Speculations
I am indeed a fan of 'Star Trek'! However, I'm not sure I understand; I thought it was generally accepted that nothing escapes from black holes, except for Hawking radiation. How do you relate it to Heisenberg's principle?