Munim

no

i am new to this forum, it got mixed up, and i dont know how to delete a question posted

.

What is the nature of the motion of light with respect to itself? Does it experience time and displacement?

The attached is an another way to clarify the problem

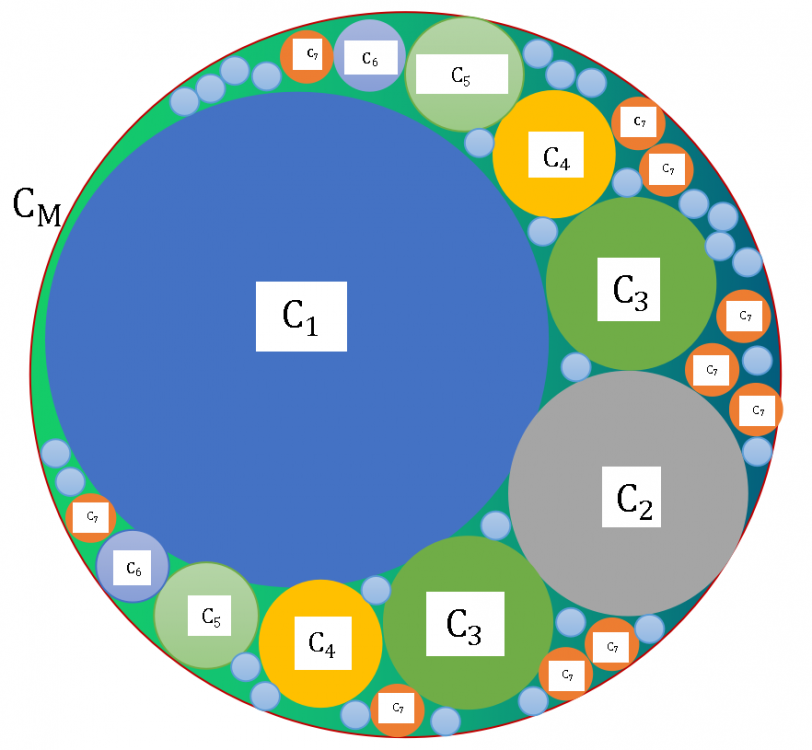
The problem is to solve for the least number of circles Ci that can be drawn inside the circle CM. So, we need the least number of circles eg. C1,C2,C3,...,C8 ( as shown in the attached image of the problem) i.e. the value of n=8 for a certain value of L (L<1). Following the image attached to the post, we are looking for the least number of circles Ci, that is, in the image we had to use up to C8, so, the total n=8, which is the supposed least value of i for a certain value of L. Furthermore, we had to use C1 once and C2 also once because we cannot fit more than one of them each, BUT, we can fit two of C3, C4, C5 and C6 and ten C7 circles. By the condition stated we cannot draw one C3, C4, C5, C6 nor can we draw less than ten C7. We have to maximize the number of certain size of circles until there is not enough space left to fit that particular size of circle. If we run out of space for C7, we start drawing C8 ( the smaller blue button sized circles) and eventually if we run out of space for C8, we have to try fitting C9=L9.AM. But if the space left after fitting circles up to C8 is not enough to fit even one C9 circle, then we have reached the end of solution for that value of L. It is not any problem I have ever seen anywhere else. It is an unique problem I thought of. You can easily visualize this problem for values suppose L=0.5, because there is just one circle that can be fitted (there is a limiting value for L<0.5 for which there is just one solution of n, which is another problem to solve) as the next circle C2=0.5*AM is impossible to be fitted inside CM. But as L moves on towards zero, the value of n increases.

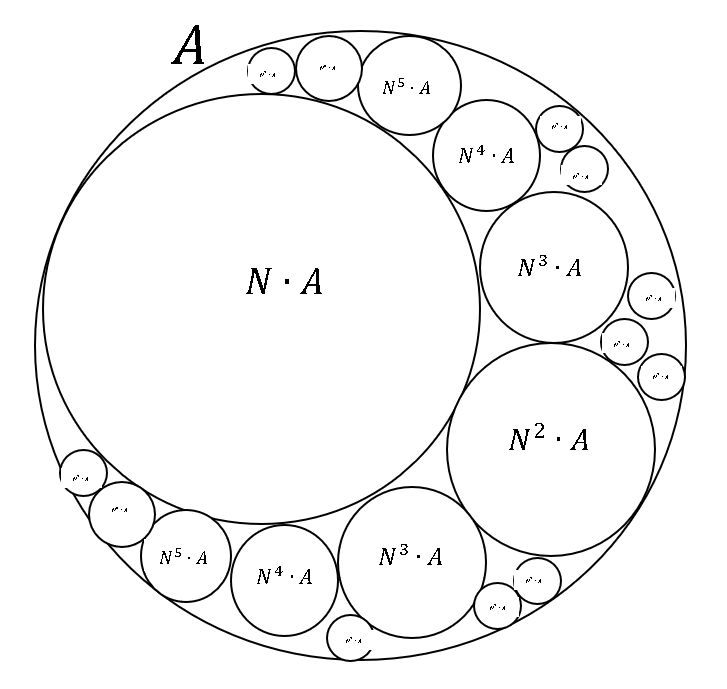
PROBLEM STATEMENT: What is the least number of circles Ci that can be fitted inside a circle CM under the following conditions i.e. solve for the least value of n for a certain (L, i): 1. The circles Ci cannot share a common area. 2. The areas of the circles Ci must be Ai=Li*AM (where, L<1 & i=1,2,3,...n; AM=area of circle CM). 3. The system must contain the maximum number of circles Ci of the same area as possible. A representation of the problem is attached to the post. NB: It's an alternate statement to my previous post

It will be a relatively simple solution for segments as I can vaguely visualize that but not for circles.

PROBLEM STATEMENT: What is the least number of smaller circles that can be fitted inside a mother circle under the following conditions: 1. The smaller circles cannot intersect or be contained inside any other circle besides the mother circle. 2. The areas of the smaller circles must be N (N<1) times any existing circle inside the mother circle. 3. The system must contain the maximum number of circles of the same area as possible. MUNIM'S PROBLEM.docx